如何实现一个卷积函数
本文,我们使用 C++ 来实现一个简单的卷积运算函数。卷积运算我们都不陌生了,它的过程其实就是卷积核在矩阵上面滑动,每停留一次就将卷积核及其所覆盖的区域进行 element-wise 相乘并求和,所有这样的求和结果就构成了输出矩阵的元素。
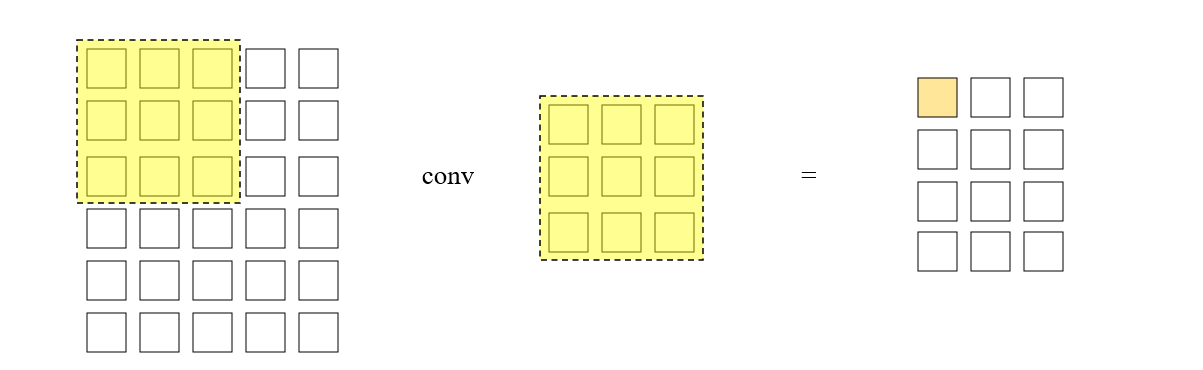
为了提高卷积运算的性能,采用并行计算的思想,我们可以令不同位置的卷积核同时开算,在足够理想的情况下,任意尺寸的矩阵卷积时间复杂度都将是 (\mathcal{O}(1))。
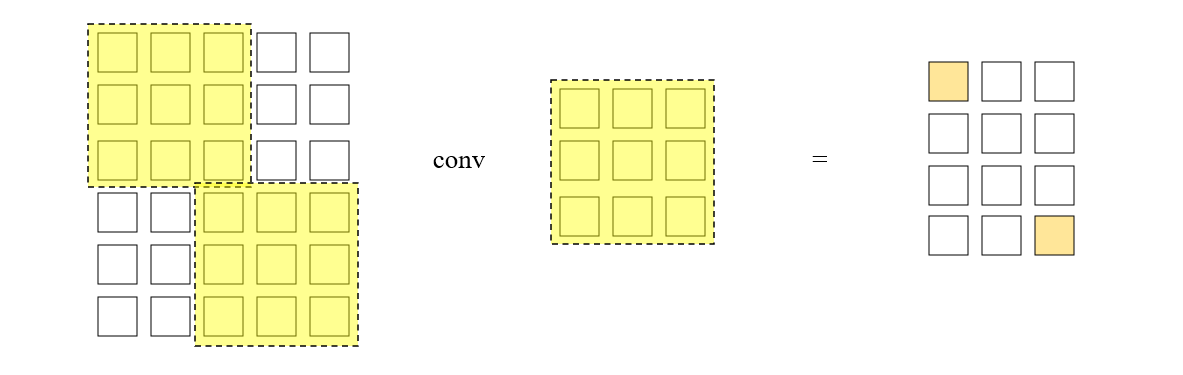
另一方面来看,单个卷积核的运算过程本质上可以看作是一维向量的点积。于是我们可以把卷积核及其所覆盖的矩阵块都展开成一维向量,然后使用向量点积来代替前述的 element-wise 相乘并求和。而这个矩阵展开的过程就叫做 im2col,通过 im2col,我们可以把卷积运算问题转化为矩阵乘法问题,在之前这篇文章和这篇文章中有详细叙述。现在,假设我们实现 im2col 方法和矩阵乘法 matmul,接下来的问题就是如何利用这两个方法实现一个我们自己的卷积层,为了方便说明,我们把 im2col 和 matmul 的方法签名定义在这里
/**
* @param data_im The image tensor.
* @param im_c The number of channels in the image.
* @param im_h The height of the image.
* @param im_w The width of the image.
* @param kh The height of the kernel.
* @param kw The width of the kernel.
* @param ph The padding size of vertical direction.
* @param pw The padding size of horizontal direction.
* @param sh The kernel stride of vertical direction.
* @param sw The kernel stride of horizontal direction.
* @param data_col The output tensor.
* @param col_w The width of the output tensor.
* @param col_h The height of the output tensor.
* **/
void im2col(const float* data_im,
const int im_c,
const int im_w,
const int im_h,
const int kw,
const int kh,
const int ph,
const int pw,
const int sh,
const int sw,
float* data_col,
const int col_w,
const int col_h);
void matmul(float* A, float* B, float* C, int M, int N, int K);
卷积运算的方法签名也很直接
/**
* @param input The input tensor.
* @param channels The number of channels in the input tensor.
* @param width The width of the input tensor.
* @param height The height of the input tensor.
* @param weights The kernel tensor.
* @param kernel_size The size of the kernel, with width equals to height.
* @param kernel_num The number of kernels, also the output channel of convolution.
* @param stride The stride of the kernel.
* @param padding The padding size of the input tensor.
* @param output The output tensor.
* @param output_width The width of the output tensor.
* @param output_height The height of the output tensor.
*/
void conv2d(const float* input,
const int channels,
const int width,
const int height,
const float* weights,
const int kernel_size,
const int kernel_num,
const int stride,
const int padding,
float* output,
const int output_width,
const int output_height);
根据前文所述,卷积运算变换后的矩阵乘法如下图所示
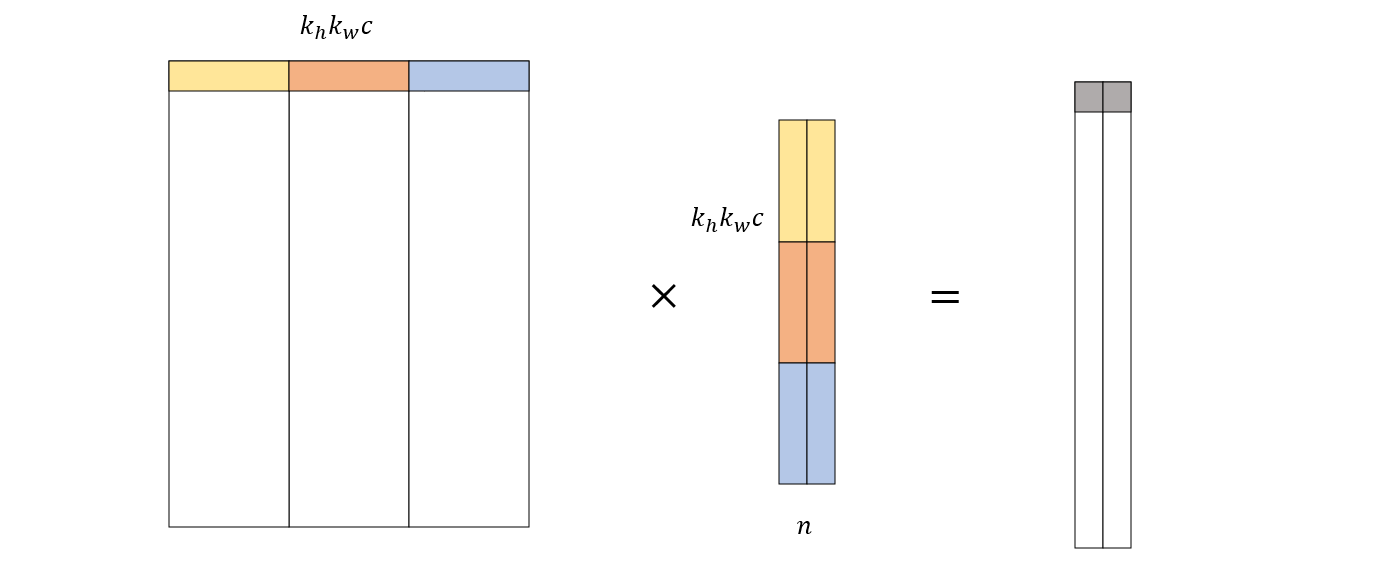
其中左边的矩阵就是 data_col。中间的矩阵是由所有卷积核变换而来的,其中变换过程如下
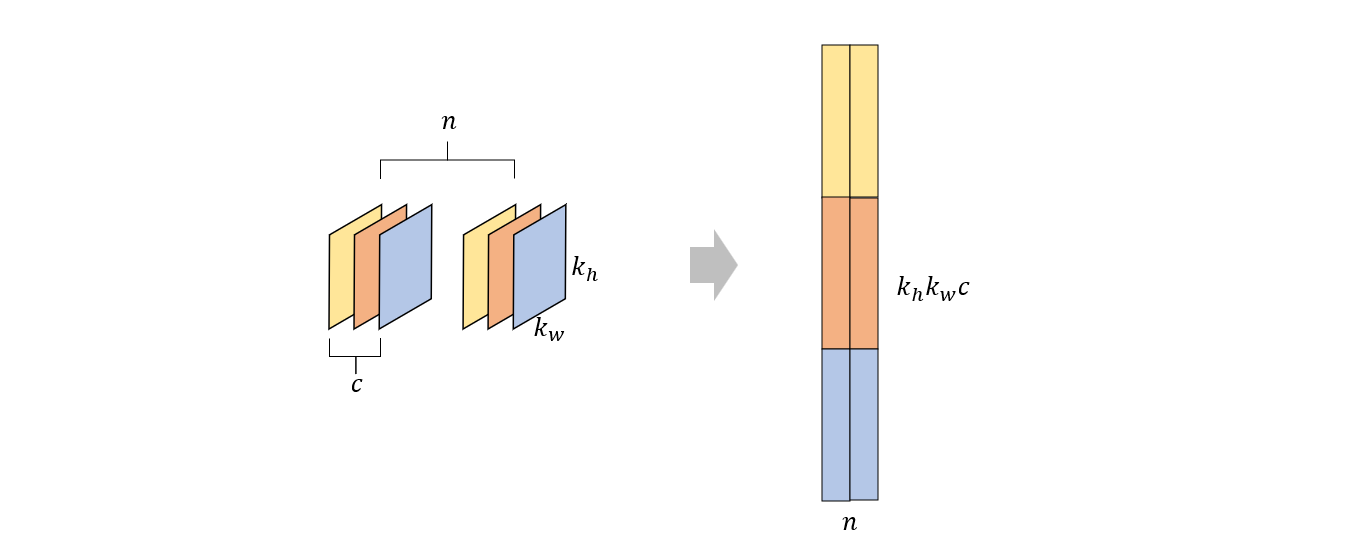
由于任意维度的张量在我们的程序中都是一维存储的,所以变换之前的卷积核阵列的存储形式是下面这样的
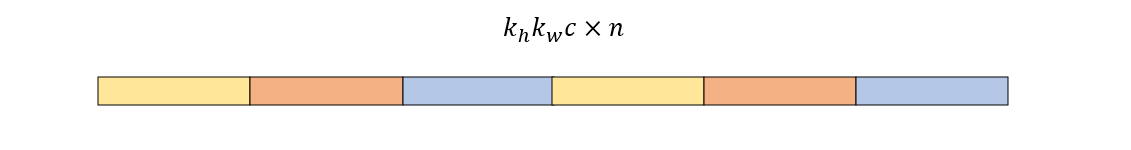
若将其看作是二维数组 \(n \times k_h k_w c\),那么它的逻辑结构又如下

显然,为了将其变换到目标形式,我们只需要对它进行转置即可。另一方面,完成矩阵乘法之后,我们还需要把结果矩阵变换到正常的张量形式
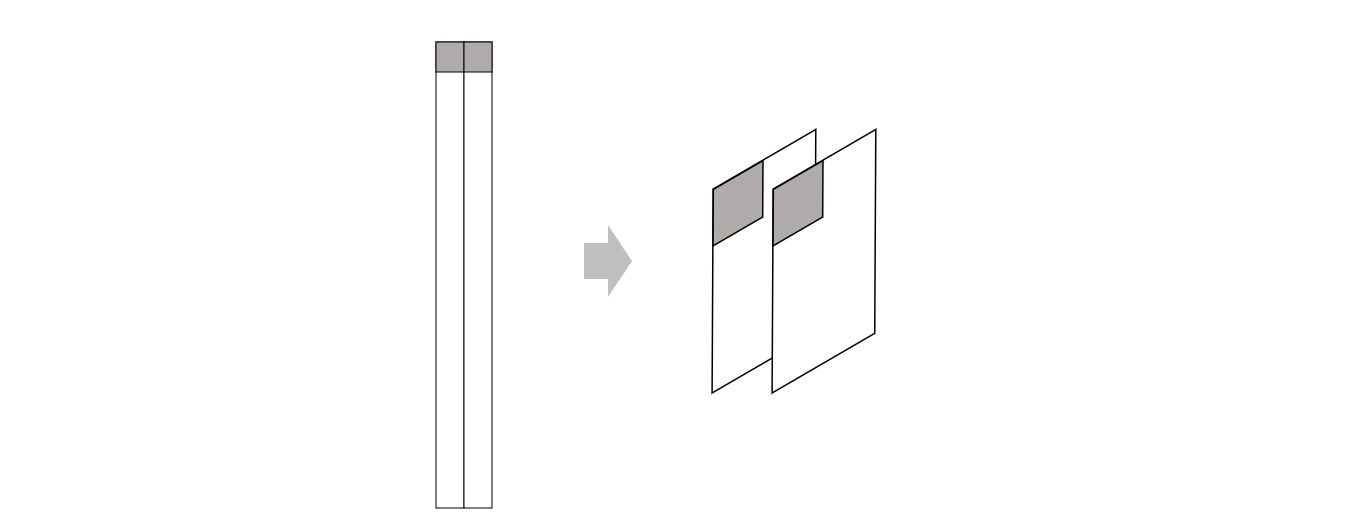
上图左边的矩阵在内存中的存储形式仍然是一维连续的

为了将其变换到目标输出形式,我们同样要对它进行转置。所以我们可以实现一个简单的转置函数
void transpose(const float* matrix, int row, int col, float* matrix_t) {
for(int i = 0; i < row; i++) {
for(int j = 0; j < col; j++) {
matrix_t[j * row + i] = matrix[i * col + j];
}
}
}
然后根据上面的分析,我们给出卷积方法的实现
void conv2d(const float* input,
const int channels,
const int width,
const int height,
const float* weights,
const int kernel_size,
const int kernel_num,
const int stride,
const int padding,
float* output,
const int output_width,
const int output_height) {
int col_h = ((height - kernel_size + padding * 2 + 1) / stride) * ((width - kernel_size + padding * 2 + 1) / stride);
int col_w = channels * kernel_size * kernel_size;
float* data_col = (float*)malloc(sizeof(float) * col_h * col_w);
im2col(input, channels, width, height, kernel_size, kernel_size, padding, padding, stride, stride, data_col, col_w, col_h);
float* weights_t = (float*)malloc(sizeof(float) * kernel_num * col_w);
transpose(weights, kernel_num, col_w, weights_t);
// data_col: col_h x col_w
// weights_t: col_w x kernel_num
matmul(data_col, weights_t, output, col_h, kernel_num, col_w);
float* output_t = (float*)malloc(sizeof(float) * col_h * kernel_num);
transpose(output, col_h, kernel_num, output_t);
}
最后,我们使用 pytorch 简单对比验证一下:
channels = 2
width = 4
height = 5
kernel_size=3
kernel_num = 2
stride=1
padding=1
weights = torch.FloatTensor(np.arange(0, channels * kernel_num* kernel_size**2).reshape(kernel_num, channels, kernel_size, kernel_size))
conv2d=torch.nn.Conv2d(channels, kernel_num, kernel_size, (stride, stride), padding)
conv2d.weight = torch.nn.parameter.Parameter(weights)
inputs = torch.FloatTensor(np.arange(channels * width * height).reshape(channels, height, width))
inputs = inputs.unsqueeze(0)
print(conv2d(inputs))
## output
## tensor([[[[ 1435.8663, 2143.8662, 2263.8662, 1487.8663],
## [ 2204.8662, 3260.8662, 3413.8662, 2222.8662],
## [ 2636.8662, 3872.8662, 4025.8662, 2606.8662],
## [ 3068.8662, 4484.8662, 4637.8662, 2990.8662],
## [ 1855.8663, 2683.8662, 2767.8662, 1763.8663]],
##
## [[ 3236.0149, 4952.0146, 5288.0146, 3576.0149],
## [ 5337.0146, 8121.0146, 8598.0146, 5787.0146],
## [ 6633.0146, 10029.0146, 10506.0146, 7035.0146],
## [ 7929.0146, 11937.0146, 12414.0146, 8283.0146],
## [ 5384.0146, 8084.0146, 8384.0146, 5580.0146]]]],
## grad_fn=<ThnnConv2DBackward0>)
void test_conv2d() {
int im_c = 1;
int im_h = 5;
int im_w = 5;
int kernel_size=3;
int padding = 1;
int stride=1;
int kernel_num = 2;
float* input = (float*)malloc(sizeof(float) * im_c * im_h * im_w);
for(int i = 0; i < im_c * im_h * im_w; i++) {
input[i] = i;
}
float* weights = (float*)malloc(sizeof(float) * kernel_size * kernel_size * kernel_num * im_c);
for(int i = 0; i < kernel_size * kernel_size * kernel_num * im_c; i++) {
weights[i] = i;
}
int output_w = (im_w - kernel_size + 2 * padding) / stride + 1;
int output_h = (im_h - kernel_size + 2 * padding) / stride + 1;
float* output = (float*)malloc(sizeof(float) * output_h * output_w * kernel_num);
for(int i = 0; i < output_h * output_w * kernel_num; i++) {
output[i] = 0;
}
conv2d(input, im_c, im_w, im_h, weights, kernel_size, kernel_num, stride, padding, output, output_w, output_h);
}
// output
// 1436.0 2144.0 2264.0 1488.0
// 2205.0 3261.0 3414.0 2223.0
// 2637.0 3873.0 4026.0 2607.0
// 3069.0 4485.0 4638.0 2991.0
// 1856.0 2684.0 2768.0 1764.0
// 3236.0 4952.0 5288.0 3576.0
// 5337.0 8121.0 8598.0 5787.0
// 6633.0 10029.0 10506.0 7035.0
// 7929.0 11937.0 12414.0 8283.0
// 5384.0 8084.0 8384.0 5580.0
可以看到,除了 pytorch 的精度问题,两者的输出几乎是一样的。