使用 C++ 实现 im2col 操作
在上一篇文章中,我们介绍了 im2col 的基本概念,知道 im2col 是一种把图像卷积运算转换成矩阵乘法的巧妙方法。本篇文章我们将想办法自己动手实现一个 im2col 操作。首先定义函数
/**
* @param data_im The image tensor.
* @param im_c The number of channels in the image.
* @param im_h The height of the image.
* @param im_w The width of the image.
* @param kh The height of the kernel.
* @param kw The width of the kernel.
* @param ph The padding size of vertical direction.
* @param pw The padding size of horizontal direction.
* @param sh The kernel stride of vertical direction.
* @param sw The kernel stride of horizontal direction.
* @param data_col The output tensor.
* @param col_w The width of the output matrix.
* @param col_h The height of the output matrix.
* **/
void im2col(const float* data_im,
const int im_c,
const int im_w,
const int im_h,
const int kw,
const int kh,
const int ph,
const int pw,
const int sh,
const int sw,
const float* data_col,
const int col_w,
const int col_h);
总的来说,im2col 需要把图像张量 data_im 转换成一个列表示矩阵 data_col,期间不做任何数值上的运算,也就是说,要把 data_im 上的每个元素拷贝到 data_col 上正确的位置去。从编程实现的角度来看,我们有两种方式,第一种方式是找一个 kh x kw 大小的窗口在 data_im 上滑动,并且每停留一次,就把窗口中的元素拷贝到 data_col 的对应位置上。另一种方式正好相反,遍历目标矩阵 data_col,然后计算当前元素在 data_im 上的位置,然后填充。两种方式的计算量都是一样的,只不过前者是一个四重循环(图片两个维度,卷积核两个维度),后者是一个二重循环,所以为了令代码更简洁,大多数实现都是选的后者。
为了简单起见,下面我们先以单通道图片为例进行叙述
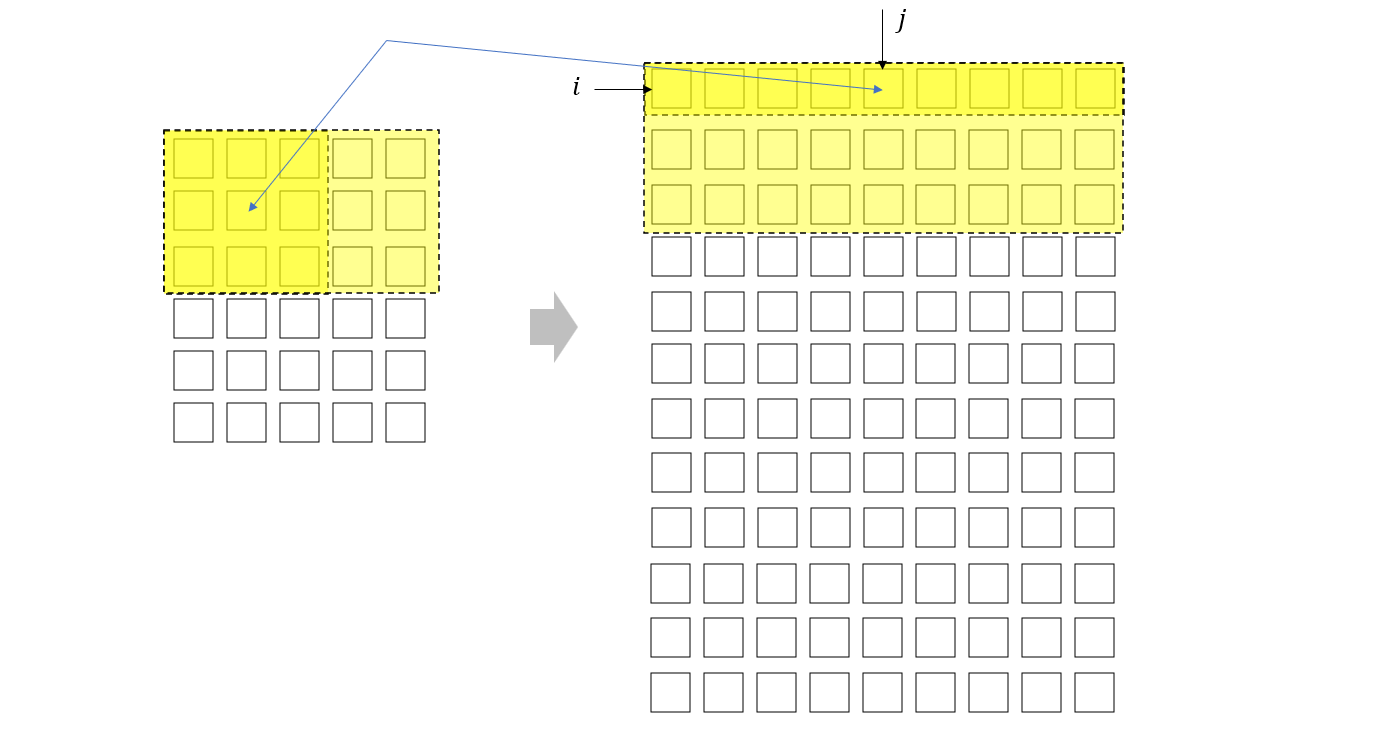
既然选择以 data_col 作为遍历对象,那么我们就需要一个公式来计算 data_col 与 data_im 的位置对应关系,从图中可以看到 data_col 的行索引 \(i\) 决定了滑动窗口(也就是卷积核)在 data_im 上停留的位置,而列索引 \(j\) 则决定了元素在窗口上的位置。
根据 im2col 的输入参数,我们可以计算滑动窗口在 data_im 水平方向和竖直方向上的停留次数分别如下
\[\begin{aligned} win_w = \frac{im_w + 2 p_w - k_w + 1}{s_w}\\ win_h = \frac{im_h + 2 p_h - k_h + 1}{s_h} \end{aligned}\]那么 data_im 上水平方向第 x 个,竖直方向第 y 个滑动窗口与 data_col 的行索引 \(i\) 的关系就如下等式
\[i = y \times win_w + x\]反过来,如果知晓了 \(i\),那么 \(x, y\) 可以用下面的代码计算
win_w = (im_w + 2 * pw - kw + 1) / sw;
x = i % win_w;
y = i / win_w;
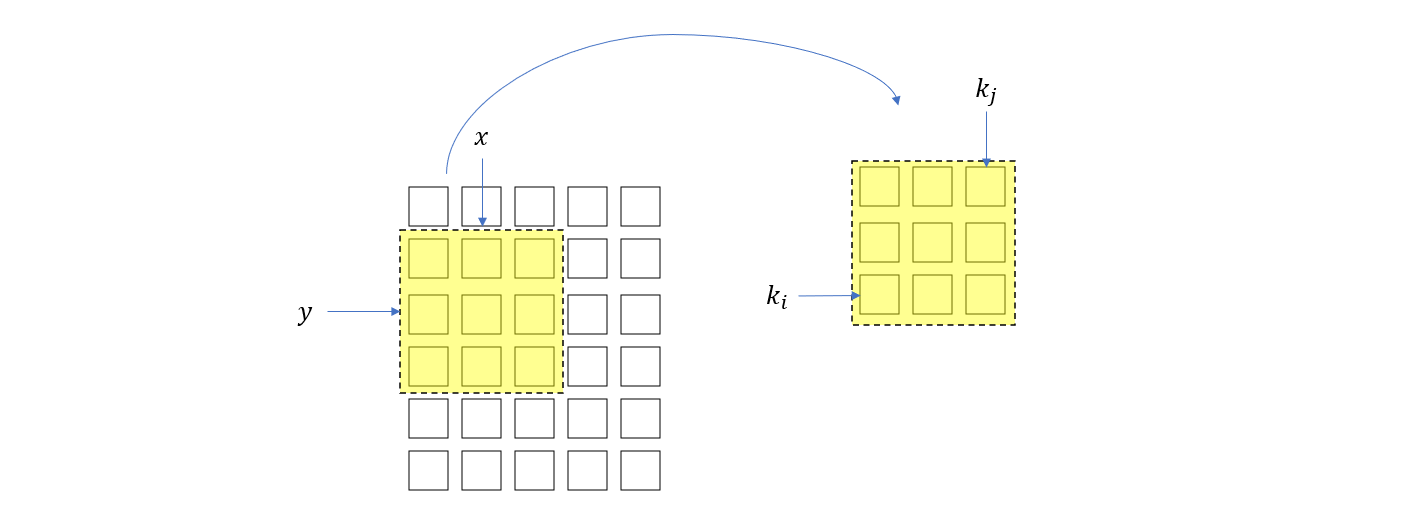
另一方面,data_col 上的列索引 \(j\) 与滑动窗口上第 \(k_i\) 行,第 \(k_j\) 列元素的位置关系如下式
\[j = k_i \times k_w + k_j\]所以如果知晓了 \(j\),则 \(k_i, k_j\) 可以用下面的代码计算
kj = j % kw;
ki = j / kw;
再通过 \(x, y, k_i, k_j\),我们就能确定 data_im 上的元素位置,首先,可以确定滑动窗口左上角的元素在 data_im 上的位置为 \((y \times s_h, x\times s_w)\),然后再加上窗口内元素相对于左上角的偏移量 \(k_i, k_j\),得到元素在 data_im 上的位置
row = y * sh + ki;
col = x * sw + kj;
最终我们得到单通道图片下,data_col 与 data_im 的赋值关系
data_col[i * col_w + j] = data_im[row * im_w + col];
接下来,对于多通道图片,情况要稍微复杂一点,在计算 data_col 与 data_im 的位置映射关系时,除了行和列,还需要考虑通道编号。
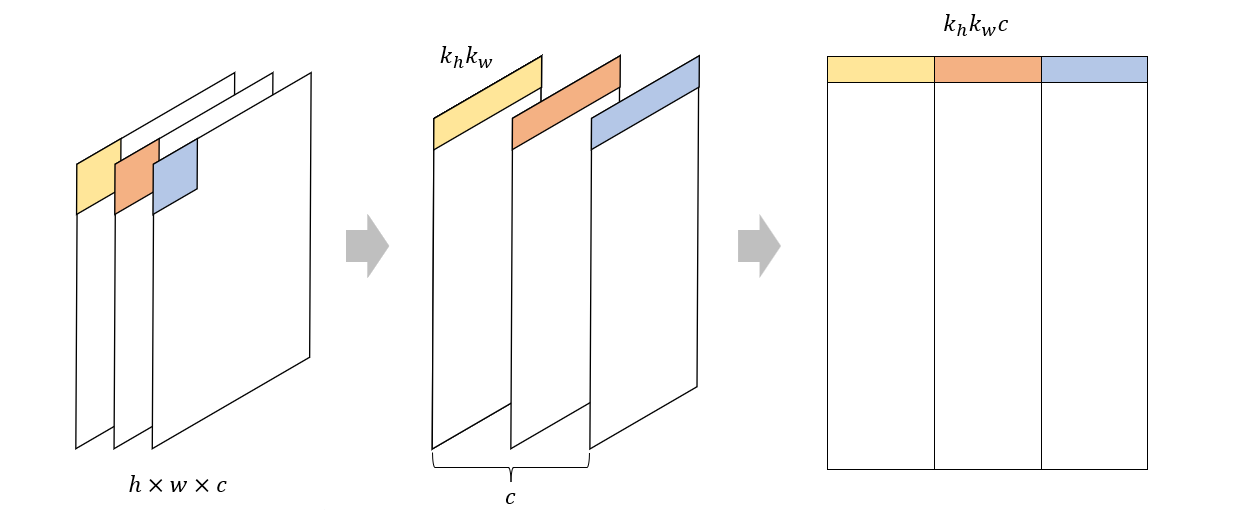
现在我们就以上图为参考,按照类似的思路来推导,首先,data_im 的任意通道上,水平方向为 x,竖直方向为 y 的滑动窗口与 data_col 的行索引 i 的关系仍然为
\[i = y \times win_w + x\]另一方面,在第 c 个通道上,滑动窗口上第 \(k_i, k_j\) 个元素在 data_col 上的列索引为
\[j = (k_h \times k_w) \times c + k_i \times k_w + k_j\]于是给定 \(i, j\),通过下面的代码计算 \(c, x, y, k_i, k_j\)
win_w = (im_w + 2 * p_w - k_w + 1) / s_w;
x = i % win_w;
y = i / win_w;
c = j / (kw * kh);
k_i = (j - c * kw * kh) / kw;
k_j = (j - c * kw * kh) % kw;
同样地,通过 \(x, y, k_i, k_j\) 确定元素在 data_im 每个通道上的位置
row = y * sh + ki;
col = x * sw + kj;
于是对于多通道图片来说,data_col 与 data_im 的位置映射关系如下
data_col[i * col_w + j] = data_im[c * im_w * im_h + row * im_w + col];
值得注意的是,如果 padding 值大于 0,我们可以使用一点技巧避免真的去填充 data_im,如下图所示
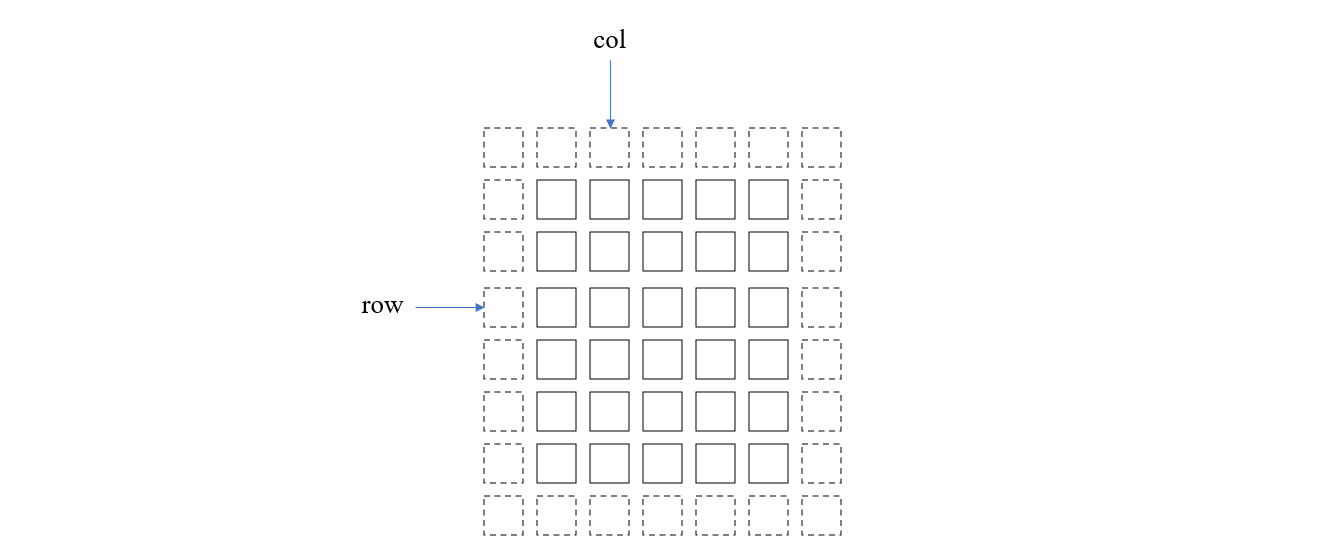
虚线部分是填充的元素,在上面计算的 row 和 col 是基于填充后的图片张量的,而真实的坐标应该是 \(row - p_h, col - p_w\),所以如果计算得到的真实坐标越过了 data_im 的边界,那么就说明这里是 padding 区域,直接返回 0 即可。
float get_data(float* data_im, int c, int im_w, int im_h, int row, int col, int ph, int pw) {
row = row - ph;
col = col - pw;
if(row < 0 || row >= im_h || col < 0 || col >= im_w) {
return 0;
}
return data_im[c * im_w * im_h + row * im_w + col];
}
最后我们给出完整的代码
void im2col(const float* data_im,
const int im_c,
const int im_w,
const int im_h,
const int kw,
const int kh,
const int ph,
const int pw,
const int sh,
const int sw,
float* data_col,
const int col_w,
const int col_h) {
// win_w and win_h are the stop times of the kernel in the image.
int win_w = (im_w + 2 * pw - kw + 1) / sw;
int win_h = (im_h + 2 * ph - kh + 1) / sh;
for (int i = 0; i< col_h; i++) {
x = i % win_w;
y = i / win_w;
for(int j = 0; j < col_w; j++) {
int c = j / (kw * kh);
int kj = j % kw;
int ki = j / kw;
int row = y * sh + ki;
int col = x * sw + kj;
data_col[i * col_w + j] = get_data(data_im, c, im_w, im_h, row, col, ph, pw);
}
}
}