图解卷积运算的 im2col 算法

卷积运算是一种提取图像特征的重要算法，它通过把给定的卷积核应用到图像上，从而缩减图像尺寸，达到提取特征的目的。卷积核在图像上每移动一次就对其覆盖的区域进行一次运算，具体的算法其实就是对应元素相乘然后求和，如果把参与运算的两个小矩阵 flatten 成一维的向量，那么这就是一次点积运算，正是因为这样的性质，使得卷积运算可以转换成矩阵乘法，从而利用现成的高性能矩阵乘法库实现对卷积的加速。下图展示了典型的卷积运算过程

如果我们把图像按卷积运算顺序分解成独立的小矩阵块

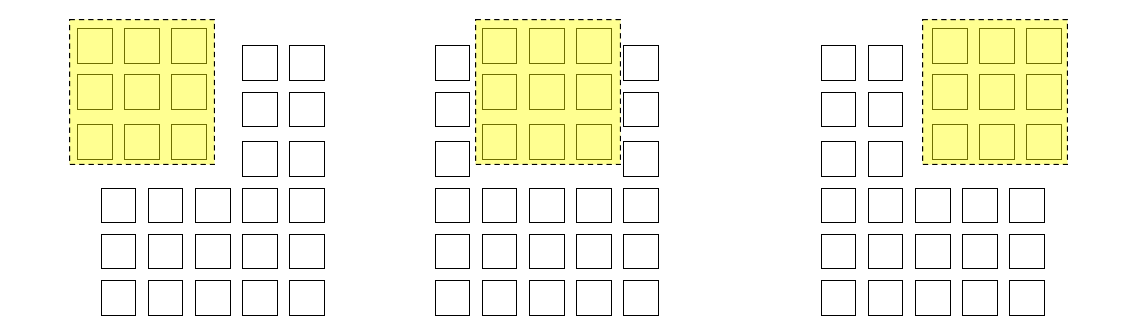
然后把每个小矩阵块 flatten 成行向量，再叠在一起，得到如下图所示的大矩阵

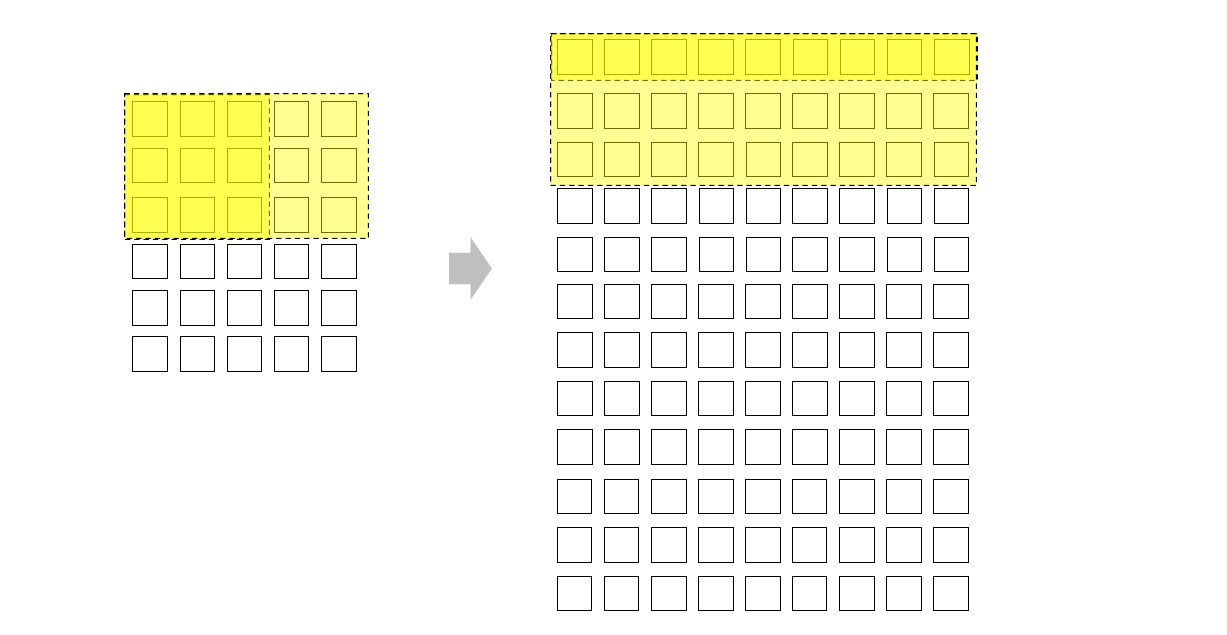
这就是所谓 im2col 过程，或者说 image to column，右边的展开矩阵就是图像的列表示形式。若假设图像尺寸为 \(h\times w\)，卷积核尺寸为 \(k_h\times k_w\)，那么卷积核在图像上的每次停留，都会在列表示矩阵上添加一个 \(k_wk_h\) 的向量，不难发现，卷积核总共停留了 \((h-k_h+1)(w - k_w+1)\) 次，所以图像转换成列表示矩阵的尺寸就为 \(((h-k_h+1)(w-k_w+1))\times k_wk_h\)。另一方面，卷积核在图像上的每次停留都对应于输出特征图上的一个元素，也就说，图像的列表示矩阵的行数也等于输出特征图的元素数量。之所以提这一点，是因为有不少现成算法是按输出特征图的大小来计算列表示矩阵的行数的，我们在看源码的时候应该注意。

若此时我们再将卷积核 flatten 成列向量，让列表示矩阵与之相乘，得到一个向量，这其实就是输出特征图的一维表示。

以上，考虑的是单个卷积核作用于单个图像上的情况，而在神经网络的卷积层中，两者通常都是多对多的关系。这里我们假设输入通道为 c，输出通道为 n，那么卷积算法过程如下图所示

也就是说，每个卷积核都会与输入图片做对应通道的卷积运算，运算结果在通道方向上相加，得到 n 个通道的输出特征图。接下来我们考虑把上述过程转换成矩阵乘法形式。

首先，利用同样的方法，将每个通道的图像转换成列表示矩阵，然后在水平方向上拼接，如下图所示

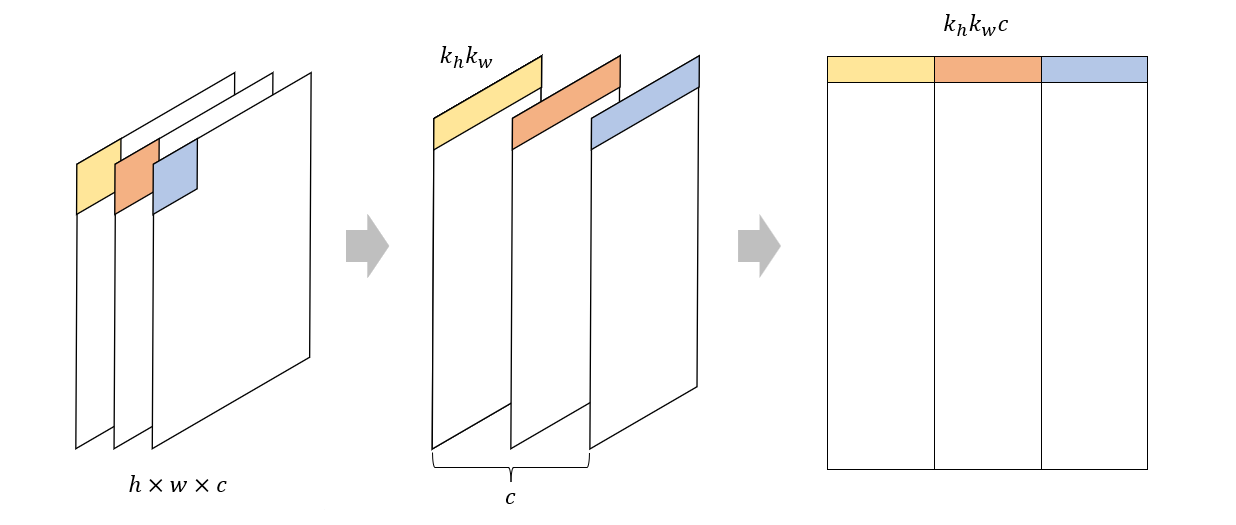
对于每个卷积核来说，也展开成一维向量。由于此时有多个卷积核，所以需要将它们在列方向上拼接成矩阵

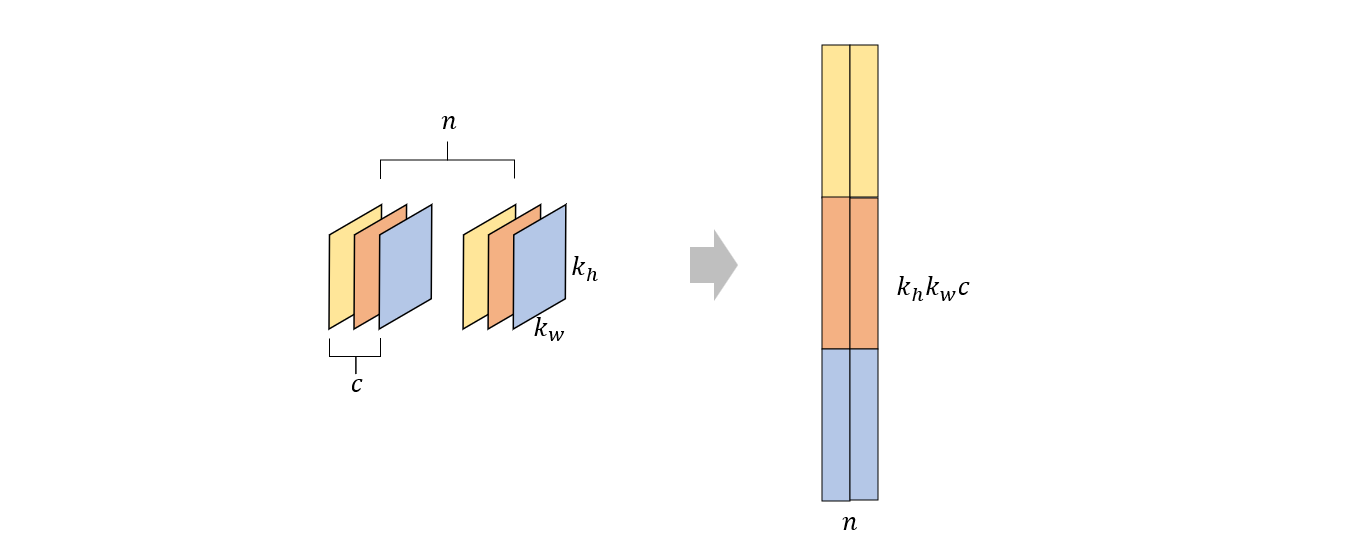
然后，让列表示矩阵和展开后的卷积核进行矩阵相乘

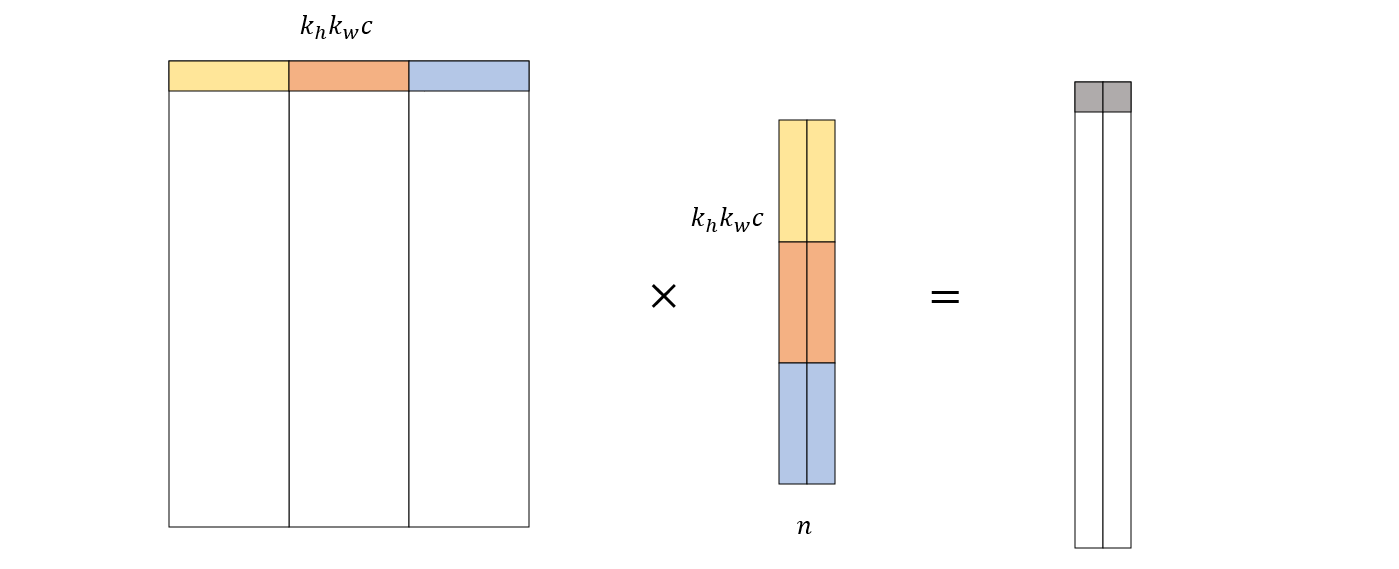
这与前面的卷积运算得到的结果是一样的，唯一的区别在图中的维度表现形式，但由于在编程的时候它们都是一维数组，所以实质没有区别。

接下来，我们再考虑有 padding 和 stride 的情况，padding 是对图像进行扩充，stride 是卷积核在图像上移动的步长，它们共同决定了输出特征图的空间维度。令 padding 分别等于 \(p_h, p_w\), stride 分别等于 \(s_h, s_w\)，我们来计算单通道图像转换成矩阵的尺寸，首先，padding 之后的图像大小变成了 \((h+ 2 * p_h)\times (w + 2 * p_w)\)，而由于卷积核在竖直和水平方向上的移动步长为 \(s_h, s_w\)，那么卷积核在图像上停留的次数为 \(\frac{h+ 2 * p_h - k_h + 1}{s_h} \times \frac{w+2 * p_w-k +1}{s_w}\)，当然这是建立在 s 可以被整除的情况下，否则需要向下取整。

最后我们再总结一下，im2col 将图像转换成列表示矩阵，可以利用高度优化矩阵乘法库来加速卷积运算。本文主要介绍 im2col 是怎样实现这种转换的，并且也探讨了为何这种转换是有效的。