关于 Transformer 架构的详细分析
在阅读本文之前,可能需要一些前置知识,以防对文中符号和公式感到困惑。
自注意力机制
在 Seq2Seq 模型中,引入的注意力机制着眼于建立输出值与输入序列各单词的关联关系,以最简单的 Seq2Seq 结构为例,权重值的计算依赖于输入单元和输出单元。如下图所示,在计算注意力向量\(c_t\) 的时候,\(h_1\) 的权重 \(\alpha_{t1}\) 依赖于输入隐层单元 \(h_1\) 和输出隐层单元 \(h’_{t-1}\)。
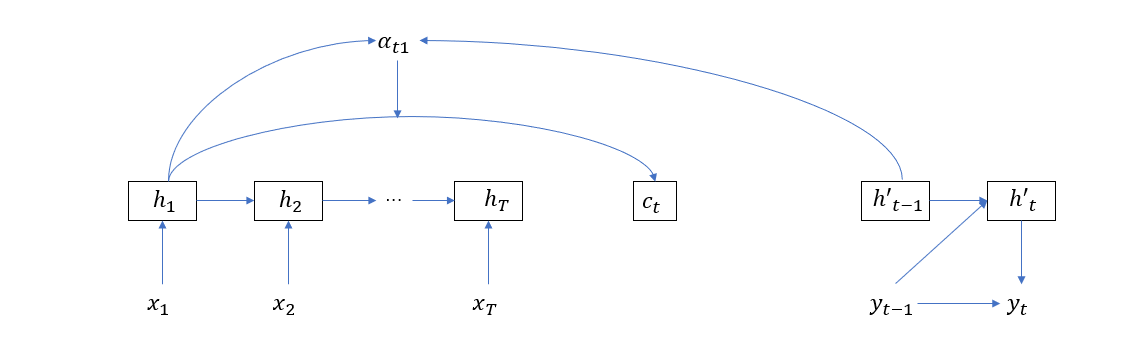
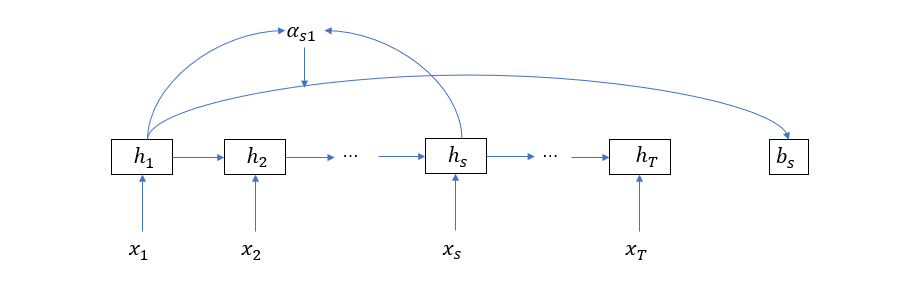
而自注意力则关注输入序列或输出序列各单词内部的关联关系,如果非要用和上图类似的模式,那么自注意力的计算将如下图所示(作为区分,我们用 \(b_s\)表示关于第 \(s\) 个单词的自注意力)
在前文的讨论中,我们已经知道了输入输出之间的注意力的计算公式为
\[c_j = \sum_{i=1}^T \alpha_{ji} h_i = H \alpha_j^\top\]也就是隐层的加权平均,这里的 \(\alpha_j\) 代表了输入输出间的注意力权重。那么自注意力的计算也可以写成同样的形式
\[b_j = \sum_{i=1}^T \alpha_{ji} h_i = H \alpha_j^\top\]只不过此时 \(\alpha_j\) 代表的是输入单元之间的注意力权重,它的计算形式为
\[\alpha_j^\top =softmax(e_j)\]其中
\[\begin{aligned} e_j^\top &= [e_{j1}\quad e_{j2}\quad \dots\quad e_{jT}]\\ &= [h_j^\top h_1\quad h_j^\top h_2\quad \dots\quad h_j^\top h_T]\\ &= h_j^\top H \end{aligned}\]而这里的 \(e\) 就是对齐函数,我们可以把它定义为向量点积形式
\[e_{ji} = h_j^\top h_i\]经过一通代入后,可以得到自注意力的矩阵计算形式
\[b = H \cdot softmax(H^\top H)\]计算图如下
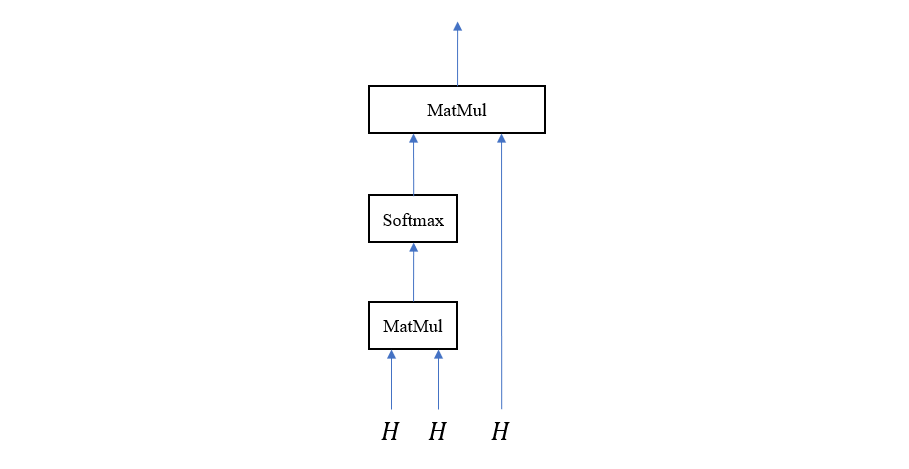
由于我们采用了点积对齐模型,所以这种注意力模型也叫点积注意力 (Dot-Product Attention)
Transfomer 的自注意力模块
来自 google 的论文 Attention Is All You Need 提出了一种被称为 Transformer 的新的 Encoder-Decoder 结构。它的特点是以注意力模块作为基本计算单元,而不是像之前的模型那样以 RNN 或者 LSTM 等结构作为基本构建块。所以这篇论文的名称就很有意思,如果事先不了解情况,会觉得不知所云,但实际上它的内涵很简单,那就是只保留注意力机制,或者更明确地说——使用注意力模块代替 RNN / LSTM 单元。下面我们就来看看 Transfomer 是如何从之前的 Encoder-Decoder 结构一步一步演化过来的(note:下面提到的这些网络结构不一定都是真实存在的,而是我们为了最终能得到 Transformer 而进行的实验,在某种程度上,这些结构反映了论文的作者们思维过程)。首先,我们给出传统的不带注意力机制的 Encoder-Decoder 网络
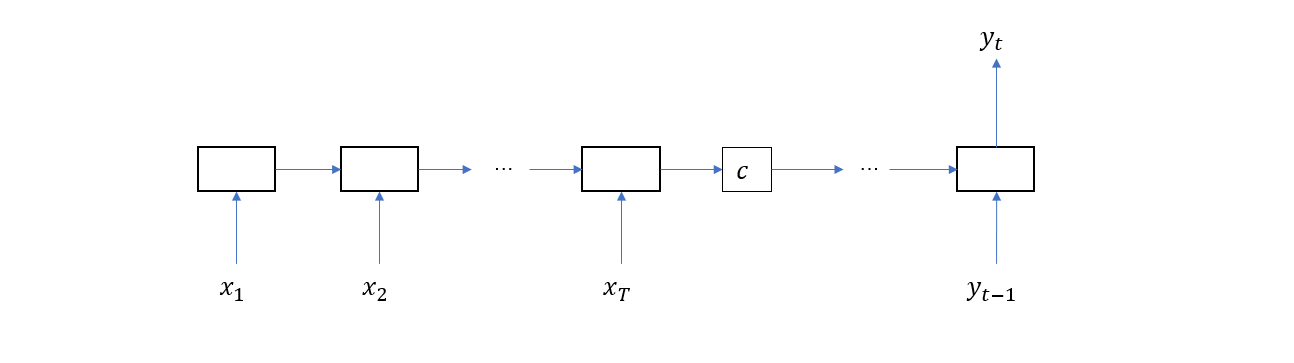
然后是带注意力机制的 Encoder-Decoder 网络(note:这里只画出了 \(c_t\) 的其中一个依赖节点)

接下来是带自注意力机制的 Encoder-Decoder 网络,为了区别注意力向量,这里我们用 \(b_s\) 代表第 \(s\) 个输入单词相关的自注意力向量

这里再多说几句,self-attention 是我们根据 attention 的计算过程而类比出来的,当我们在 attention 的上下文中讨论时,\(c_t\) 是整个输入单词和第 \(t\) 个输出值的语义关系向量。而在 self-attention 的情况下,\(b_s\) 是整个输入单词序列与第 \(s\) 个单词的语义关系向量。所以 attention 跨越了解码和编码阶段,而 self-attention 则仍然处于编码阶段,将完整的自注意力 Encoder 的结构画出来如下图
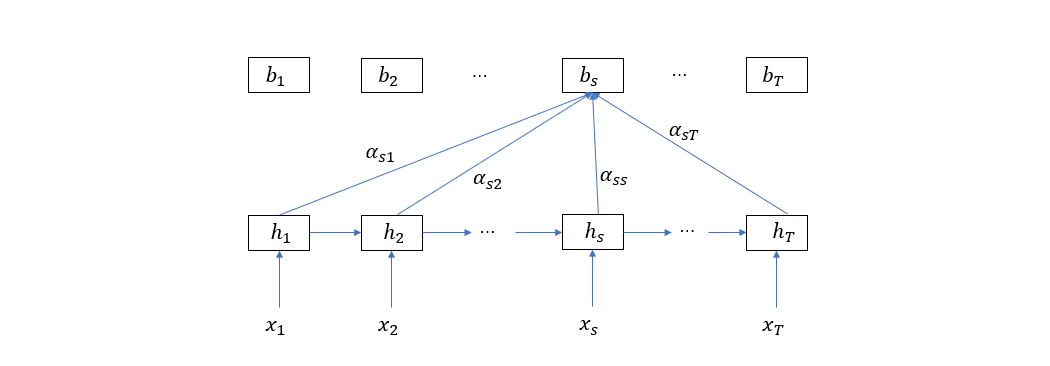
在解码阶段,自注意力向量将被用于计算注意力向量,就像之前把隐层状态用来计算注意力向量类似,补上 Decoder 的结构如下图
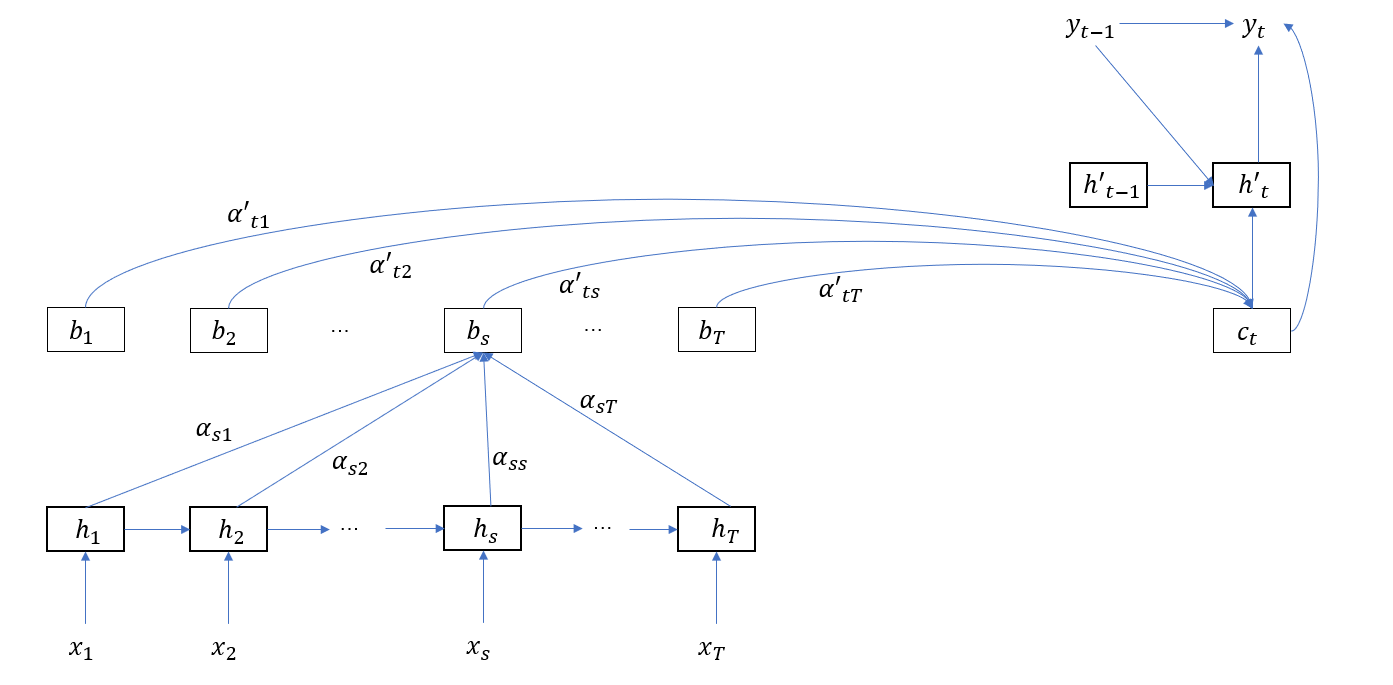
从这里就可以看出,注意力向量在 Encoder 和 Decoder 端上都单独形成了一层,这时,RNN / LSTM 隐层单元就显得有点多余,所以最后让我们删掉 RNN / LSTM 单元,仅保留注意力结构
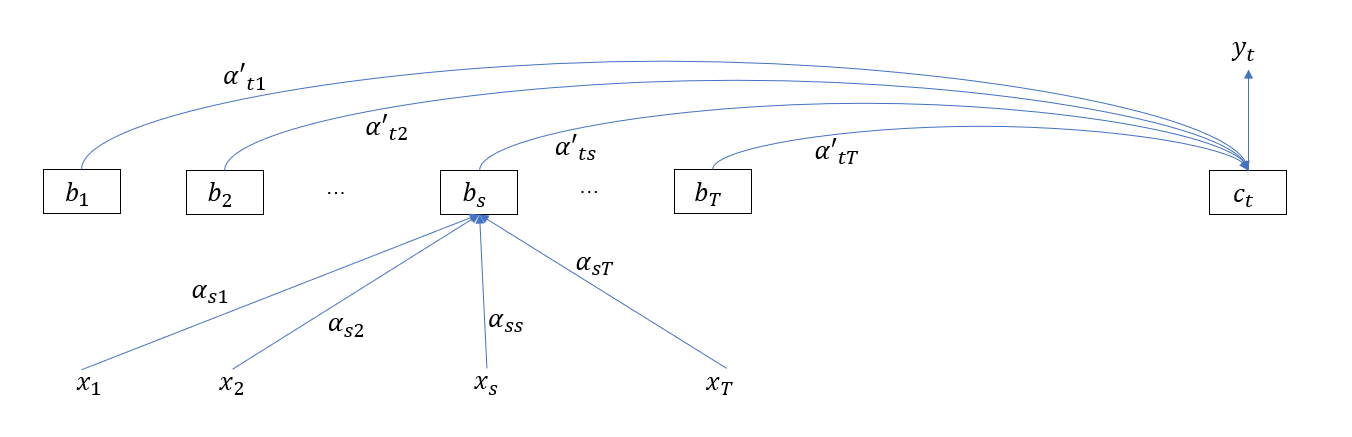
到这里,Transformer 已经颇具雏形了, 其中 \(b_s\) 的计算公式为
\[b_s = \sum_{i = 1}^T \alpha_{si} x_i\]再结合第一节的讨论,写成矩阵形式
\[b = [b_1 \quad b_2 \quad ... \quad b_T] = X softmax(X^\top X)\]其中 \(X = [x_1 \quad x_2 \quad … \quad x_T]\)。
从这里我们可以看到,去掉 RNN/LSTM 单元后,直接通过矩阵乘法就可以对输入数据进行编码,不像之前那样,首先输入 \(x_1\) 得到 \(h_1\),然后再输入 \(x_2\) 才能得到 \(h_2\),依次类推。顺序输入没有充分利用计算能力,而采用纯注意力的编码器和解码器具有更高的计算效率。
Mulit-Head 注意力
Multi-Head 注意力是以上一节介绍的点积注意力模块为基本块而组成的,它的目的是构造多个子空间的注意力向量。所以,首先需要将输入向量映射到子空间,方法是使用全连接层映射,具体表现在乘以一个矩阵 \(X_s = X W\)。假设输入向量的维度为 \(d=512\),需要构造 \(h=8\) 个子空间注意力,则每个子空间的维度为 \(64\),于是矩阵 \(W\) 的形状就为 \(512 \times 64\),子空间维度为 \(64\),将这 8 个子空间注意力向量拼接起来又得到一个 512 维的联合注意力向量。这样一来,Multi-Head 注意力的输入和输出便和普通注意力模块的输入输出统一起来了,前者可以无缝替换后者。计算图如下所示
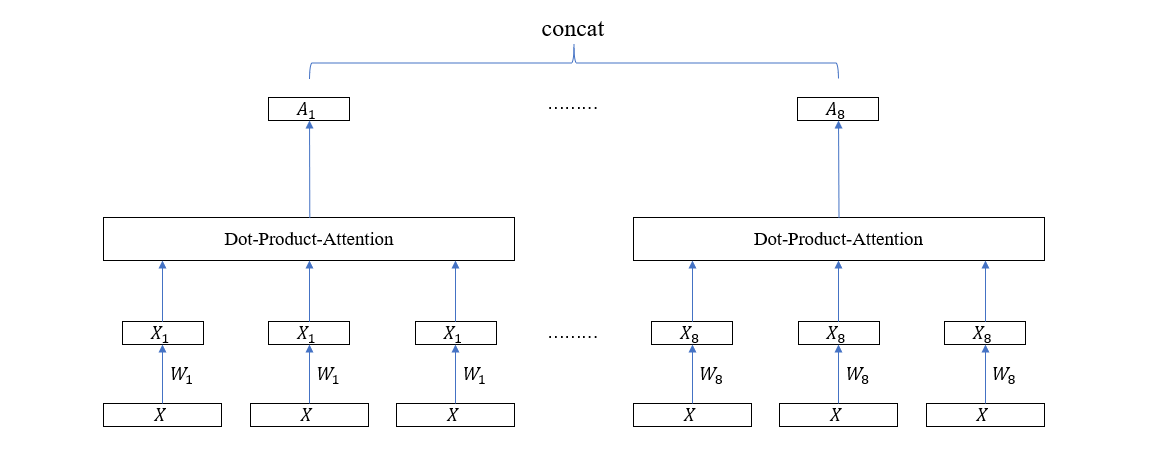
在这个计算图里面,每个 Head 的 3 个输入向量共享一个全连接层权重矩阵,但实际上,为了增强模型的泛化能力,可以独立地训练这些全连接层,于是上图可以稍微改变一下
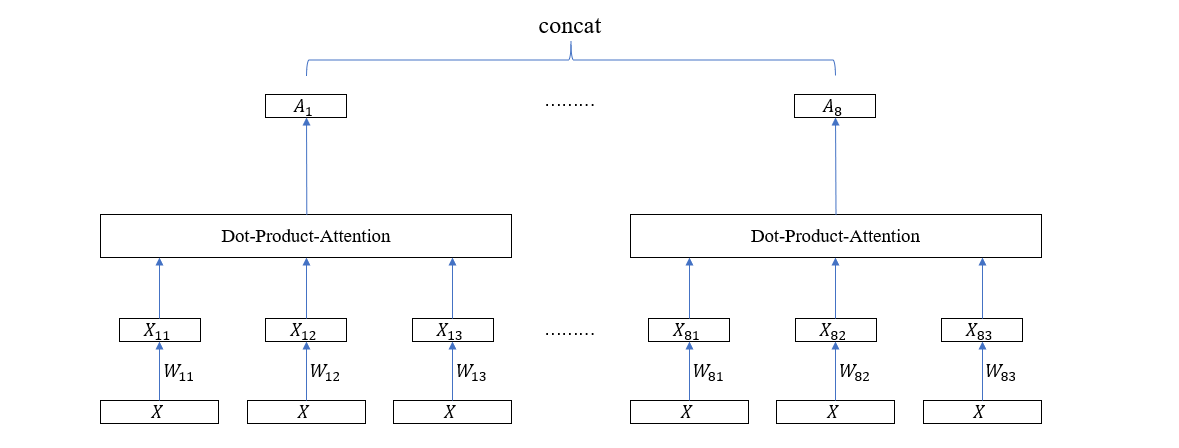
因为涉及到多个子空间的注意力向量计算,每个子空间的计算图就是一个 Head,所以这种方法就叫 Multi-Head Attention。
值得注意的是,通过不同的权重矩阵映射后,输入到 Dot-Production Attention 层的 3 个矩阵不再是同一个矩阵了,也就是说我们前面一直在说的注意力公式
\[b = H \cdot softmax(H^\top H)\]不再具有普遍意义,为此我们可以将其改写为
\[b = V \cdot softmax(K Q)\]关于 Query, Key 和 Value 的解释
下面我们稍微解释一下为什么注意力计算的三个输入分别代表 Query,Key 和 Value。首先我们把自注意力向量展开
\[\begin{aligned} b_t &= \sum_{i=1}^T \alpha_{ti} h_i \\ &= \sum_{i=1}^T \alpha_{ti} [h_{i1}\quad h_{i2} \quad ... \quad h_{in}]^\top \\ &= \left[\sum_{i=1}^T \alpha_{ti} h_{i1}\quad \sum_{i=1}^T \alpha_{ti} h_{i2}\quad ... \quad \sum_{i=1}^T \alpha_{ti} h_{in}\right]^\top \end{aligned}\]于是对于每个分量来说有
\[\begin{aligned} b_{tk} &= \sum_{i=1}^T \alpha_{ti} h_{ik}\\ &= [h_{1k} \quad h_{2k} \quad \dots \quad h_{Tk}] [ \alpha_{t1} \quad \alpha_{t2} \quad \dots \quad \alpha_{tT}]^\top\\ &= v_k \alpha_t^\top\\ &= v_k \cdot softmax(e_t)\\ &= v_k \cdot softmax(H^\top h_t) \end{aligned}\]这里我们把 \(v_k\) 定义成了 \([h_{1k} \quad h_{2k} \quad \dots \quad h_{Tk}]\)。
下面,让我们从另一个角度来解释上式的计算过程,首先给出 K-v pairs:
\[\begin{aligned} K:&\quad v_k\\ --&--\\ k_1: &\quad v_{1k}\\ k_2: &\quad v_{2k}\\ ...\\ k_T: &\quad v_{Tk} \end{aligned}\]其中每个 \(k_i\)都是向量,每个 \(v_{ik}\) 都是标量,也就是说,每个向量对应一个标量值。现在我们有一个新的向量 \(q_t\),也就是 query,它的长度和 \(k_i\) 一致,那么请问它对应的值是多少?显然,如果 query 等于向量组 keys 中的其中一个,则是能够查找出来的。但问题在于,如果 query 不在 keys 中,那么它的值就是未定义的。为了解决这一困难,一种被称为软寻址的方法被提了出来,相对于普通查找,软寻址的 query 不必在 keys 中,而是通过计算 query 与 keys 的相似度(也就是 \(\alpha_t\)),来合成一个值,具体的方法是,如果 query 和某个 key (\(k_i\)) 的相似度越高,那么与这个 key 所对应的 value (\(v_{ik}\)) 的权重就越大,把所有权重算出来,再对 values 加权求和就是对应于此 query 的值。
可以看到,注意力值的计算其实就是一种软寻址,它的 keys 是 \(H^\top\),query 是 \(h_t\),values 是 \(v_k\)。如果是批量软寻址,那么 query 就是 \(H = [h_1 \quad h_2 \quad ... \quad h_T]\),value 就是 \(V = [v_1 \quad v_2 \quad …\quad v_n]^\top\)。另外不难发现,这里的 \(H^\top\) 和 \(V\) 互为转置关系。
Transformer 的 Encoder-Decoder 结构
在第二节,我们从传统的 Seq2Seq 一路推到了以自注意力模块作为基础构建块的 Encoder-Decoder 结构,从原理上理解了 “Attention Is All You Need” 这句话的实际含义。但是,第二节给出的最终结构只能算是一个雏形,它能用,但不够好。正式的 Transformer 结构,从全局来看,分为 Encoder 和 Decoder 两个部分,其中 Encoder 接收输入序列,Decoder 接收 Encoder 的中间表示 和 上一轮的输出序列并预测下一个单词,如下图所示
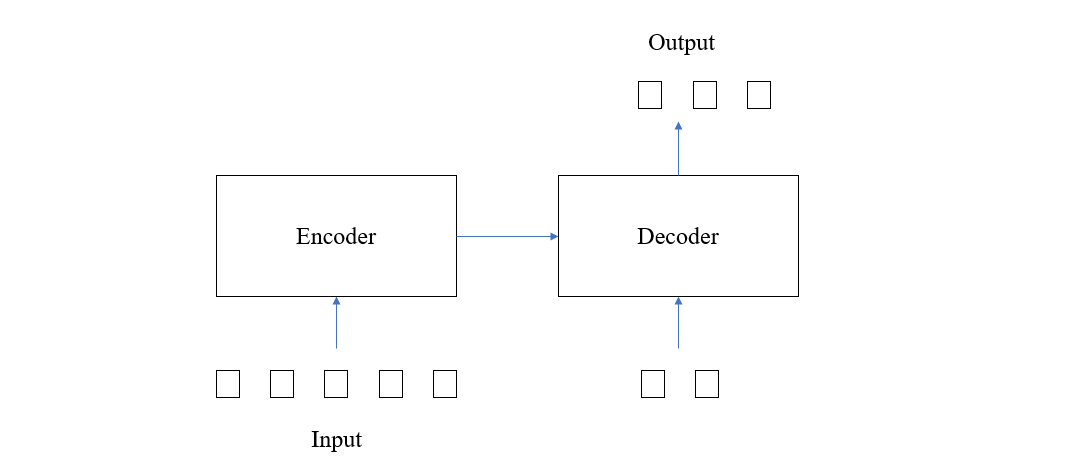
这里的 Decoder 同以往的 Seq2Seq 结构类似,也需要利用前面产生的单词来计算后面的单词,不同的地方在于,在 Seq2Seq 结构中,因为一次只能输入一个单词,所以只能通过 \(y_{t-1}\) 来计算 \(y_t\),而在 Transformer 中,因为可以同时输入一个单词序列,所以采用的方法是以上一轮计算的输出序列作为本次计算的输入,然后预测增加了一个单词的序列,并如此迭代,直到输出句尾标记(即<EOS>)。显然,采用这种方式的优点在于,每预测一个单词,它前面的所有单词都能起到作用。
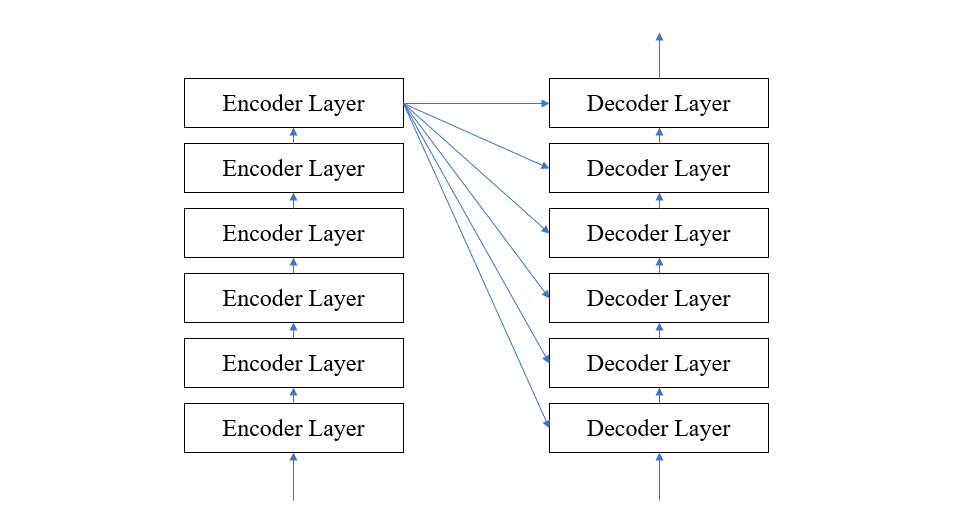
接下来我们将重点聚集到 Encoder 和 Decoder 的内部结构,如下图所示,每个 Encoder 都是由多个 Encoder Layer 组成的,前一个 Encoder Layer 的输出是后一个 Encoder Layer 的输入,Decoder 也是类似的结构,只不过每个 Decoder Layer 除了接收前一个 Decoder Layer 的输出值外,还要接收 Encoder 的输出值。
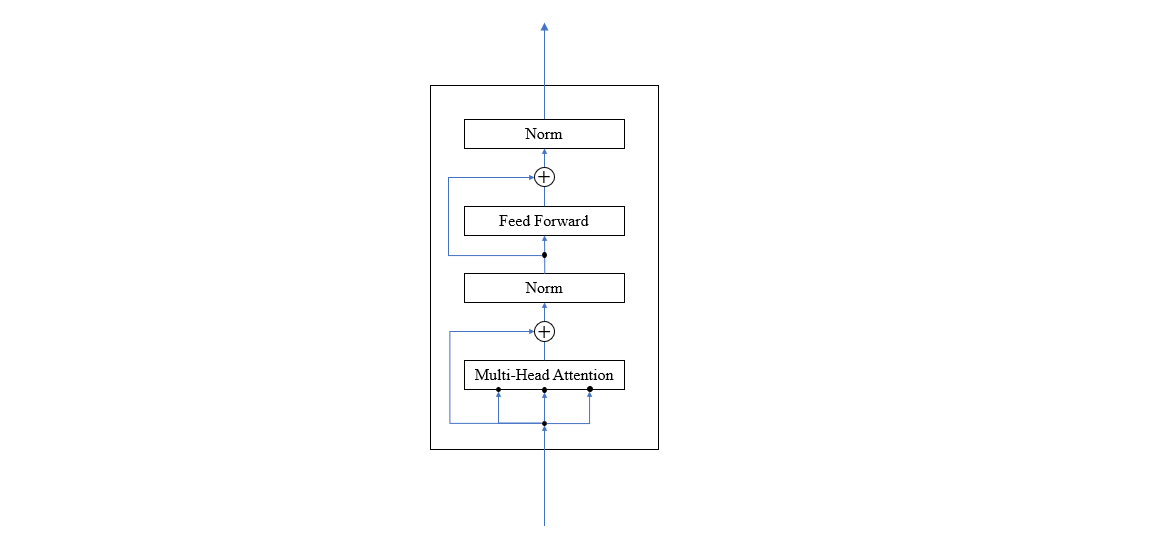
对于每个 Encoder Layer 来说,它又被分为两个主要层,第一个是我们前面讨论的注意力层(采用 Multi-Head 注意力),第二个就是普通的全连接层,并且在每个层前后还采用了残差连接,每层之后还进行了 normalzation。其结构如下图
Decoder Layer 的情况要复杂一点,它一方面要接收 Encoder 给的中间表示 \(E\),另一方面要接收上一轮的预测序列 \(P_{t-1}\)。在 Decoder Layer 中,首先将 \(P_{t-1}\) 使用注意力模块进行编码得到 Query 矩阵 \(Q\),然后令 \(E^\top\) 作为 key 矩阵 \(K\),\(E\) 作为 value 矩阵 \(V\),把它们输入注意力模块计算跨结构的注意力,最后输入全连接层,如下图所示
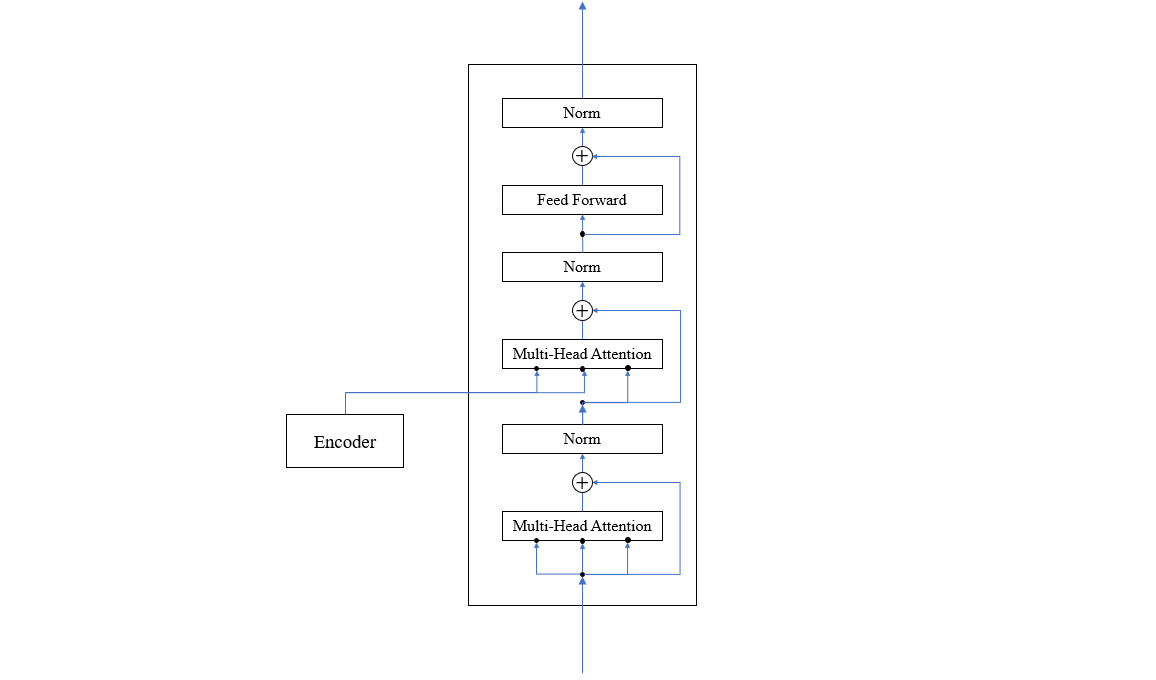
以上,就是 Transformer 的总体结构。
总结
本文首先通过对注意力结构的类比分析阐述了自注意力的思路原理;然后从软寻址的角度解释了 Query,Key 和 Value 的含义;之后阐述了抛弃 RNN/LSTM 的纯注意力模块;接下来将普通注意力从子空间分割的角度介绍了 Multi-Head 注意力的计算方法;最后给出了 Transformer 的总体架构。当然,还有一些细节没有完善,我们下一篇文章再来探讨。
参考文献: Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L. and Polosukhin, I., 2017. Attention is all you need. arXiv preprint arXiv:1706.03762.