对注意力机制的一些理解（后篇）

在上一篇文章中，不太正式地介绍了注意力机制，我们从概念上了解到注意力机制的实质是在输出每个预测单词的时候输入单词有不同的权重，本篇文章希望从算法角度来进一步解释。

基于 RNN 的 Encoder-Decoder 结构

Kyunghyun Cho 在论文 Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation 中提出了基于 RNN 的 Encoder-Decoder 结构，它的编码器是一个 RNN，在时刻 \(t\) 的隐层状态为

\[h_{t} = f(h_{t-1}, x_t)\]

其中 \(h\) 为隐层状态，\(x\) 为输入词（记住它们都是向量），将这个 RNN 在时间上展开得到如下图所示的结构

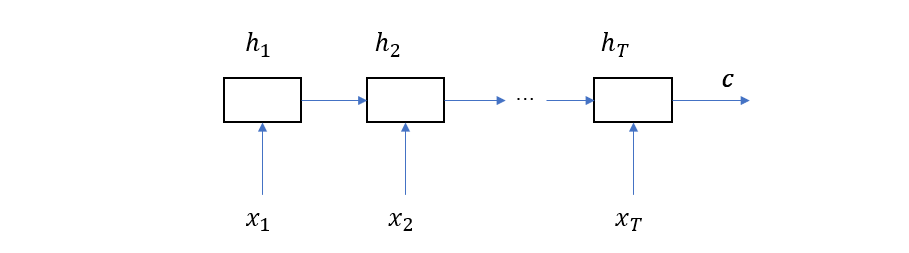
这里的 \(c\) 就是最终输出向量，也就是说，编码器的作用是将源语句的所有单词编码成一个固定长度的向量。

另一方面，解码器也是一个 RNN，它在时间上展开如下图所示

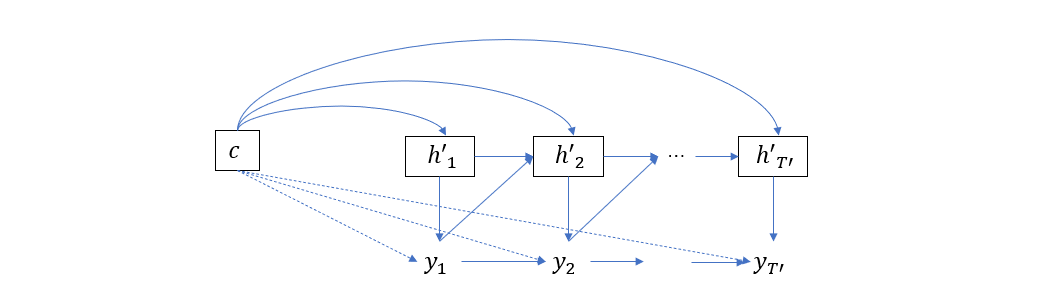
可以看到，每个时刻的隐层状态都依赖于上一个时刻的隐层状态、上一个输出词以及输入序列编码 \(c\)，于是在时刻 \(t\) 的隐层状态可以表示为

\[h'_t = f(h'_{t-1}, y_{t-1}, c)\]

而输出词则为

\[y_t = g(h'_t, y_{t-1}, c)\]

引入注意力机制后的 Encoder-Decoder 结构

上一节的 Decoder 在计算所有 \(y_t\)的时候，所依赖的 \(c\) 都是相同的，也就是说，同一个输入序列编码被用于解码所有输出单词。这一特点导致生成输出序列的每个词的时候，输入单词所占的权重没有任何变化，显然，这与常识不符。为了改进这个缺陷，Dzmitry Bahdanau 在论文 Neural Machine Translation by Jointly Learning to Align and Translate 中提出了新的想法，即令 \(y_t\) 依赖于变化的 \(c\)

\[h'_t = f(h'_{t-1}, y_{t-1}, c_t)\\ y_t = g(h'_t, y_{t-1}, c_t)\]

这时我们把解码器的图像表示稍微修改一下以阐述这种思想

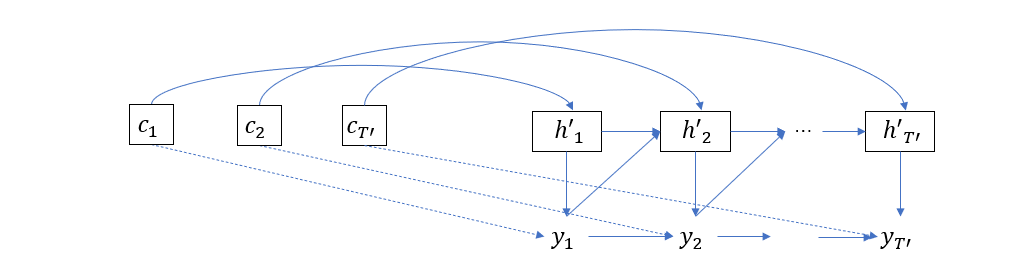
这里的 \(c_t\) 则是编码器隐层状态的加权和

\[c_t = \sum_{i = 1}^T \alpha_{ti} h_i\]

显然，输入单词对输出单词的不同影响可以通过调整权重来体现。这时编码器的结构可以修改为下图

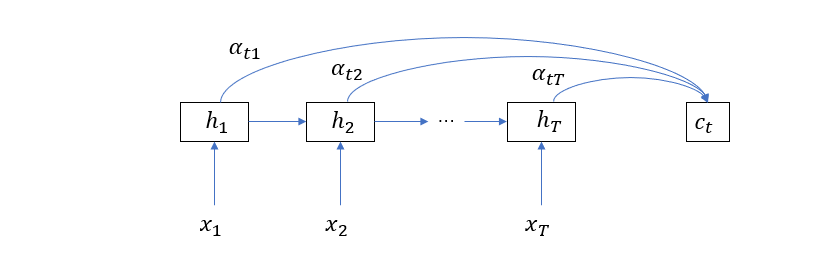
所以 \(c_t\) 向量决定了在预测输出单词 \(y_t\) 的时候，哪些输入单词应该被重点关注，这就是注意力的含义，所以 \(c_t\) 也可以被称为注意力向量。

接下来讨论权重向量 \(\alpha_t\)，依我们最直接的想法，可以把这个权重向量作为神经网络自身的参数进行训练，但是马上就可以发现这一思路不可行，一个原因是神经网络的参数是固定的，而不同的语句，其注意力模型显然是不一样的，固定的权重显然无法实现这一目标，另一个原因是不同语句的单词序列长度一般也不一样，固定大小的权重矩阵显然也不好处理。

所以在这篇论文中引入了对齐模型(alignment model)的概念，简单来说，对齐模型的目的是为了计算第 \(i\) 个输入单词所处的语义环境和第 \(j\) 个输出单词所处的语义环境的匹配程度。这里的语义环境其实就是隐层状态，因为它是对单词序列的编码，所以包含了当前单词及其环境的语义信息。

其实关于这一点我们还可以多说几句，在上述的编码器结构中，隐层状态实际上只包含了当前单词及其之前单词的语义信息，所以这里的语义信息不是很完整，而为了补充后面单词的语义信息，论文改进了编码器结构，采用双向 RNN，如下图所示

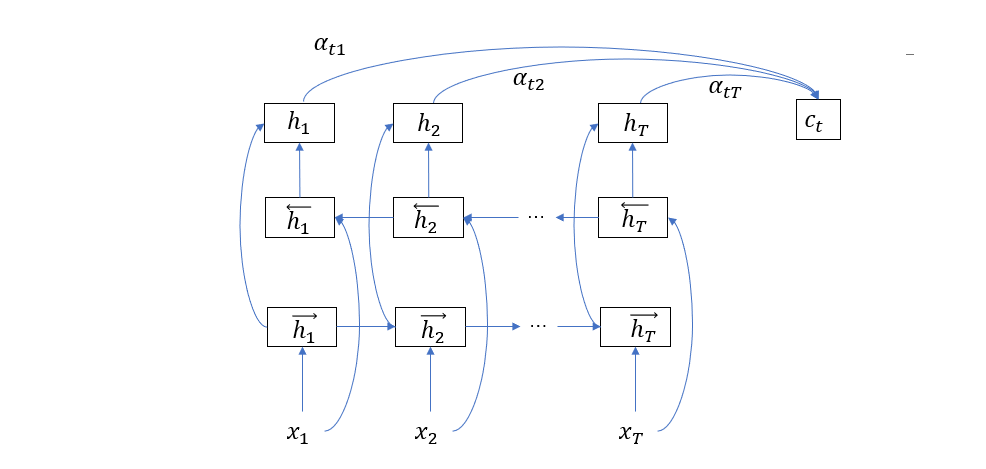
使用这种结构，\(\vec{h}_t\) 包含当前单词及其左边的语义信息，\(\leftarrow{h}_t\) 包含当前单词及其右边的语义信息，于是它们的组合 \(h_t\) 就完整地包含了当前单词的语义信息。

于是在编码器端，\(h_i\) 代表第 \(i\) 个单词的语义环境，而在解码器端，本来应该是 \(h'_j\) 来代表第 \(j\) 个单词的语义环境，但是 \(h'_j\) 本身又依赖于 \(c_j\)，为了不造成循环依赖，我们只有退而求其次地使用 \(h'_{j-1}\) 来代表第 \(j\) 个输出单词的语义环境，两者之间相差一个单词位置，所以这种替换问题不大。

定义了输入输出单词的语义环境表示之后，就可以回来定义之前提到的对齐模型了，对齐模型以第 \(i\) 个 输入单词的语义环境信息和第 \(j\) 个输出单词的语义环境信息为参数，返回一个量化的输入输出匹配度，即

\[e_{ji} = a(h_i, h'_{j-1})\]

这里的 \(e_{ji}\) 是标量，对于每个 \(j\)，定义 （注意这里我们默认 \(e_j\) 是一个列向量）

\[e_j^\top = [e_{j1}\quad e_{j2} \quad ...\quad e_{jT}]\]

然后再对 \(e_{j}\) 作 softmax 归一化变换，这就是我们刚才提到的权重向量。

\[\alpha_{j} = softmax(e_j) =\left\{ \frac{\exp(e_{ji})}{\sum_{k = 1}^T \exp(e_{jk})} \mid i = 0,1,,T\right\}\]

到这里，我们还没有说明对齐模型的具体形式，在 Bahdanau 的论文中，对齐模型使用一个前馈神经网络来表示，具体如下图

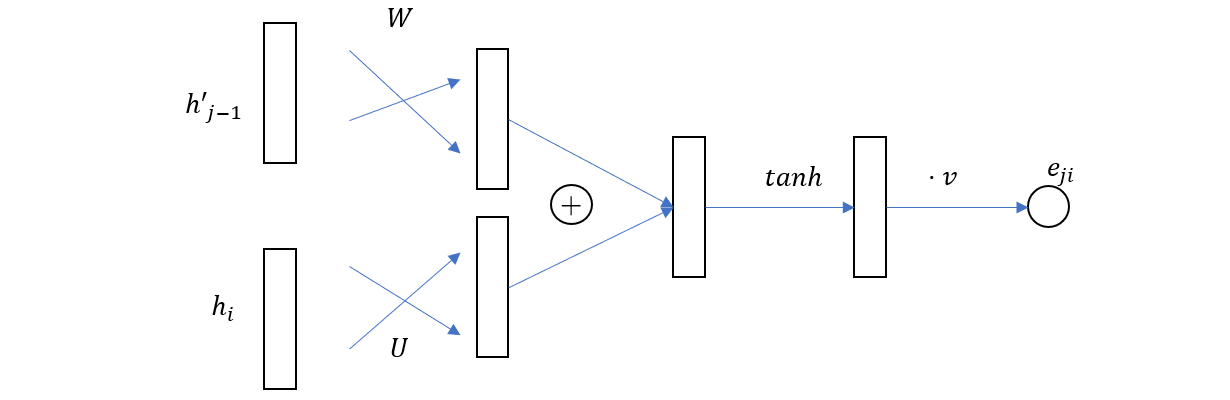
其公式如下

\[e_{ji} = v \tanh(W h'_{j-1} + U h_i)\]

其中\(W, U, v\) 都是参数，而\(W, U\) 的形状为\(m \times n\)，\(v\) 的形状为\(1\times m\)，\(n\) 为隐层向量的维度，这个小型的神经网络同总体模型一起训练，也就是该篇论文的标题 (Jointly Learning to Align and Translate) 的含义，即对齐模型与翻译模型的联合训练。

注意力计算的矩阵形式

最后，我们尝试把计算过程写成矩阵形式，首先是对齐模型

\[\begin{aligned} e_{j}^\top &= [e_{j1} \quad e_{j2} \quad ... \quad e_{jT}]\\ &= v \tanh([Wh'_{j-1} + Uh_1 \quad Wh'_{j-1} + Uh_2 \quad ... \quad Wh'_{j-1} + Uh_T])\\ &= v \tanh(W \vec h'_{j-1} + [Uh_1 \quad Uh_2 \quad ... \quad Uh_T])\\ &= v \tanh(W \vec h'_{j-1} + U[h_1 \quad h_2 \quad ... \quad h_T])\\ &= v \tanh(W \vec h'_{j-1} + UH) \end{aligned}\]

关于上式有几点需要说明，第一，为了让矩阵乘法合法，必须使\(m = T\)；第二，上式第二个等号用到了规则\([\tanh(a)] = \tanh([a])\)； 第三，这里我们用 \(\vec h'_{j-1}\) 来表示 \([{h'}_{j-1} \quad {h'}_{j-1} \quad ... \quad {h'}_{j-1}]\)，注意它只是 \(h'_{j-1}\) 在列方向上的重复了 \(T\) 次，形状为\(n\times T\)，另外 \(H = [h_1 \quad h_2 \quad … \quad h_T]\)，形状为\(n\times T\)。 然后再考虑注意力向量

\[\begin{aligned} c_j &= \sum_{i = 1}^T \alpha_{ji} h_i \\ &= \alpha_{j1} h_1 + \alpha_{j2} h_2 +... + \alpha_{jT}h_T\\ &= [h_1 \quad h_2 \quad ... \quad h_T][\alpha_{j1}\quad \alpha_{j2} \quad ... \quad \alpha_{jT}]^\top \\ &= H \alpha_j^\top \end{aligned}\]

这里 \(\alpha_j\) 的尺寸为 \(1\times T\)，\(H\) 的尺寸为 \(n \times T\)，于是可知 \(c_j\) 的尺寸为 \(n\times 1\)。最后我们再考虑由注意力向量组成的矩阵

\[\begin{aligned} c &= [c_1 \quad c_2 \quad ... \quad c_{T'}] \\ &= [H \alpha_1^\top \quad H\alpha_2^\top \quad ... \quad H\alpha_{T'}^\top]\\ & = H\alpha \end{aligned}\]

其中

\[\begin{aligned} \alpha &= [\alpha_1^\top \quad \alpha_2^\top \quad ... \quad \alpha_{T'}^\top] \\ &= softmax([e_1 \quad e_2 \quad ... \quad e_{T'}])\\ &= softmax(v \tanh([W \vec h'_0 + UH \quad W \vec h'_1 + UH \quad ... \quad W \vec h'_{T'-1} + UH ]))\\ &= softmax(v \tanh(W \mathbf{H}' + U \mathbf H)) \end{aligned}\]

这里的\(\mathbf{H}’\) 和\(\mathbf{H}\) 都是张量，尺寸为\(T’ \times n \times T\)，其中

\[\mathbf{H}' = [\vec{h}'_0 \quad \vec{h}'_1 \quad ... \quad \vec{h}'_{T' - 1}]\] \[\mathbf{H} = [H \quad H \quad ... \quad H]\]

所以最终注意力矩阵为

\[c = H \times softmax(v \tanh(W \mathbf{H}' + U \mathbf H))\]

考虑一种简化后的对齐模型

在之前的讨论中，我们使用的是 Bahdanau 原论文中的前馈网络对齐模型，但实际上，既然对齐模型是为了量化输出单词对输入单词的注意力，那更为简单的选择是直接计算两个参数向量的点积，也就是

\[a(h_i, h'_{j-1}) = {h'}_{j-1}^\top h_i\]

那么可以得到

\[\begin{aligned} e_{j}^\top &= [e_{j1} \quad e_{j2} \quad ... \quad e_{jT}] \\ &= [{h'}_{j-1}^\top h_1 \quad {h'}_{j-1}^\top h_2 \quad ... \quad {h'}_{j-1}^\top h_T] \\ &= {h'}_{j-1}^\top[ h_1 \quad h_2 \quad ...\quad h_T]\\ &= {h'}_{j-1}^\top H \qquad (1\times n) \times (n \times T) \end{aligned}\]

转置一下为

\[e_j = H^\top {h'}_{j-1}\]

其中 \({h’_{j-1}}\) 的形状为 \(n \times 1\)。

\[\begin{aligned} \alpha &= [\alpha_1^\top\quad \alpha_2^\top \quad ... \quad \alpha_{T'}^\top]\\ &= softmax([e_1 \quad e_2 \quad ... \quad e_{T'}])\\ &= softmax(H^\top[{h'}_{0}\quad {h'}_{1}\quad ... \quad {h'}_{T'-1}] )\\ &= softmax(H^\top H') \qquad (T \times n) \times (n \times T') \end{aligned}\]

其中 \(H’\) 的形状为 \(n\times T’\)，最后可得注意力矩阵

\[c = H\alpha = H \times softmax(H^\top H') \qquad n \times T'\]

总结

本文主要介绍了 Kyunghyun Cho 和 Dzmitry Bahdanau 两篇论文的主要想法，简单地说，Kyunghyun Cho 提出了基于 Encoder-Decoder 的机器翻译模型结构，而 Bahdanau 则在此基础上引入了注意力机制，以及与之相关的对齐模型。本文还尝试解释了 Bahdanau 使用双向 RNN 结构的原因，即为了获取更完整的语义从而更好地利用对齐模型。