对注意力机制的一些理解

从 RNN 说起

一个典型的前馈网络结构如下图所示

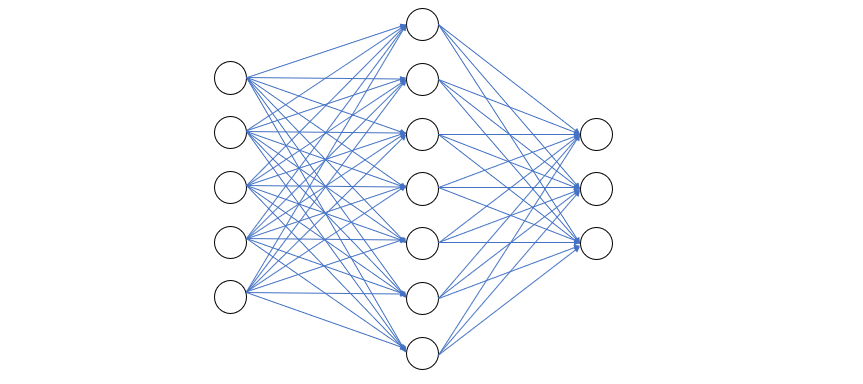
如果我们简化一下，把每层节点用一个圆圈表示，则如下图

其中 \(x, h, y\) 分别是输入向量，隐层节点值和输出向量，\(U, V\) 分别表示两层的权重矩阵。该前馈网络的计算过程如下式

\[h = f(x, U)\\ y = f(h, V)\]

这里的 \(f\) 表示前馈过程，包含了计算和激活两个部分。

以上是普通前馈网络的情况，RNN 与它的区别在于，隐层节点值一方面传向输出节点，另一方面反过来和下一个输入相结合成为新的输入量。

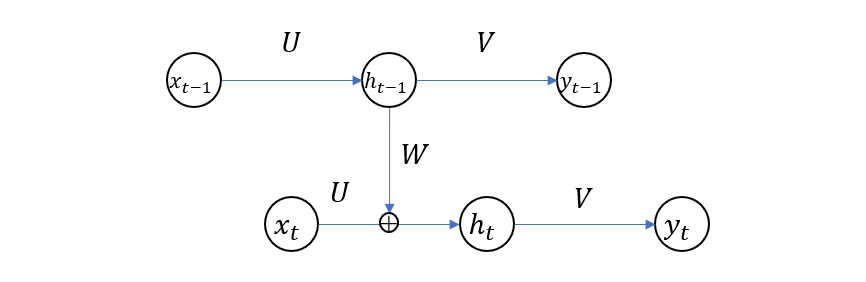
其中的 \(W\) 是隐层节点的权重矩阵。该网络的计算过程如下

\[h_t = f(x, h_{t-1}, U, W)\\ y_t = g(h_t, V)\]

可以看到，普通前馈网络的两次计算过程之间在不考虑权重更新的情况下是没有关系的，而 RNN 则多了一个反馈路径，使得每次计算的结果都受到上一次计算的影响。正是由于这种性质，使得 RNN 比较适合于建模上下文相关的序列结构，比如自然语言处理。

对于多个输入，整个结构在时间上展开的结果如下（这次我们省略了权重矩阵）

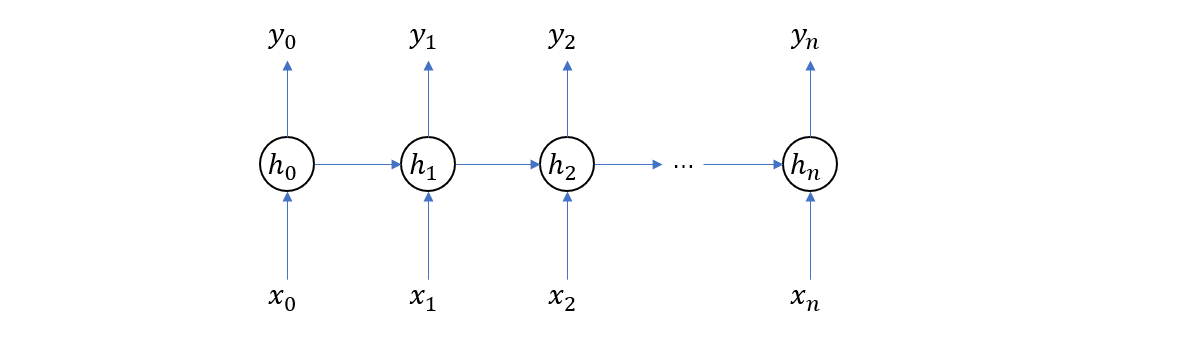
再次强调，在上图中，我们画了多个隐藏层 \(h_0,… h_n\) 是在时间上展开的结果，实际上是只有一个隐藏层的。所以，RNN 通常也可以用下图来表示

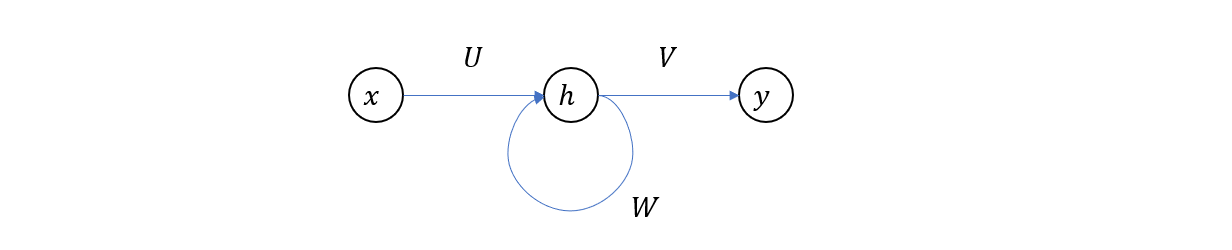
接下来我们来分析一下 RNN 的训练过程，假设一对样本的特征和标签分别为 \((x_1,x_2,…x_n)\) 和 \((\hat{y}_0, \hat{y}_1… \hat{y}_m)\)。首先，初始化权重参数，然后依次输入 \(x_0, x_1\) 直到 \(x_n\)，这时我们将得到序列 \(y_1, y_2… y_n\)，注意这里的输出与 Ground Truth 的维度不一样 n vs m，所以在计算 loss 的时候需要将不够的部分填充。最后再利用反向传播更新权重参数，这样就完成了一步计算。

神经网络机器翻译

把翻译模型看作是一个黑箱，它的输入是源语言，输出是目标语言，它们都可以被看作是由单词构成的序列（当然，这里的单词都被嵌入到了高维空间，以 embedding vector 的形式作为输入），那么翻译过程就如下图所示

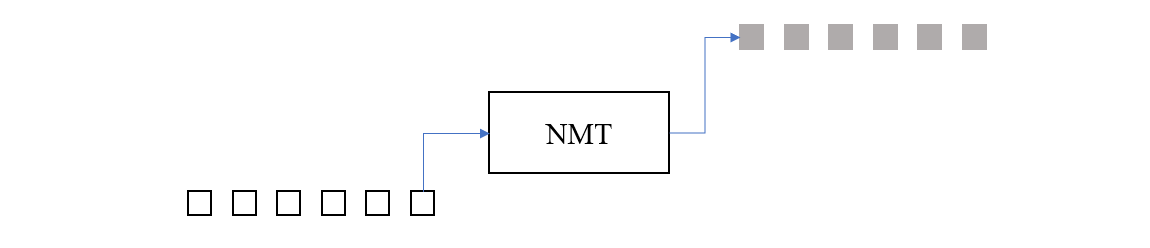
这里的神经网络翻译模型本身的实现方式有很多种，人们也在不断优化其性能。如果我们以著名的 Seq2Seq 为例，可以看到它的结构如下

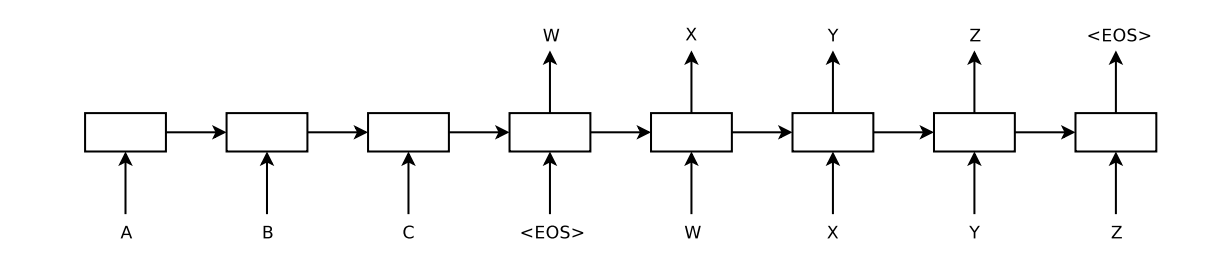
这里的 A, B, C 是输入单词序列，W, X, Y, Z 是输出单词序列，<EOS> 是语句的结束符号，中间的方框就是隐层节点。这个结构乍看起来和我们在上一节画的 RNN 在时间上展开的结构差不多，但实际上完全不一样，首先是左边部分，它的真正形式如下

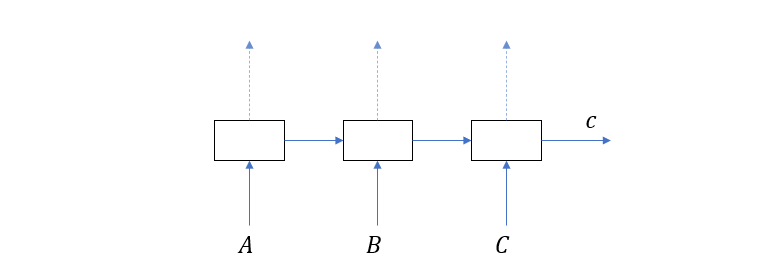
可以看到，这是一个 RNN 在时间上的展开结构，只不过它的输出量都被忽略了，整个句子被编码成了 \(c\) (取 context 之意)，所以这部分又叫做 Encoder。

右边部分也是一个 RNN 在时间上的展开，它的输入一部分是原语句编码 \(c\)，另一部分是上一次预测的结果，这与我们在确定一句不完整的话的下一个词时所用的逻辑是一样的。

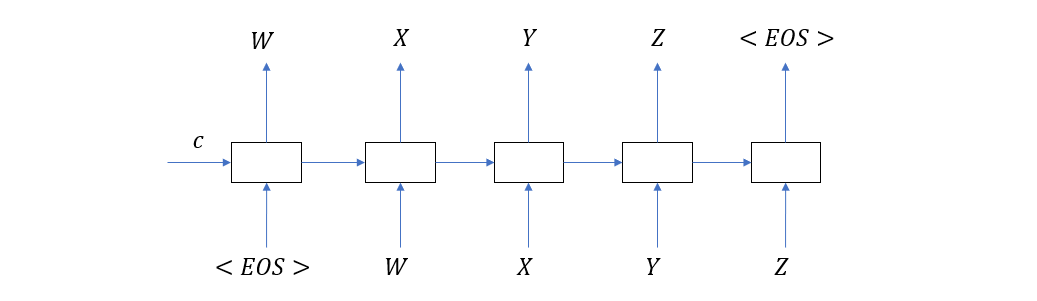
我们把 Seq2Seq 的这种结构称为 Encoder-Decoder 结构，其中左边部分为 Encoder，负责编码 input，右边部分为 Decoder，负责解码出 output。

这里我还想再强调一次，无论是 Encoder 还是 Decoder，上面的图都是在时间上的展开形式，实际上的模型应该是下面这样的

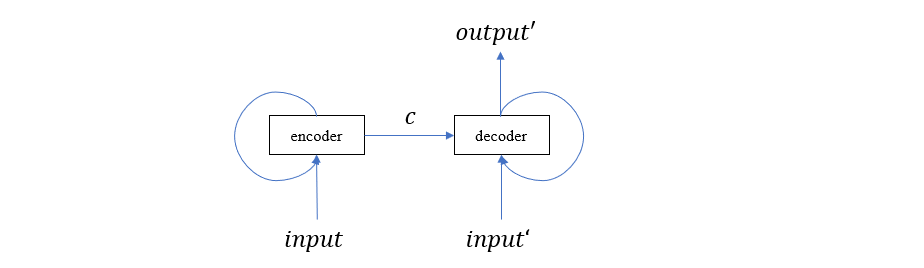
回顾我们上一节分析的 RNN 训练过程，Seq2Seq 的训练过程也是类似的，需要提及的是，在 Decoder 部分，如果某次输出产生了 <EOS>，则停止输入，到此为止产生的序列就是预测结果。

正式引入注意力机制

注意力机制的意思其实就是说，我们在预测某个位置的单词的时候，原句子的某些位置上的词应该发挥更重要的作用。举个简单的例子：

Recurrent neural networks has been firmly established as state of the art approaches in sequence modeling and transduction problems such as language modeling and machine translation.

上面这个句子加粗的两个词显然具有强烈的相关性，也就是说，在预测 language modeling 这个词的时候，sequence modeling 应该占有更高的权重。但这一想法在上一节介绍的 Seq2Seq 结构中没有得到体现，它在预测某个词的时候只用到了上一个预测词以及原句的整体编码（即c）。为了在模型中实现这一思想，一个简单的方法是在原来结构的基础上增加类似下图的连接

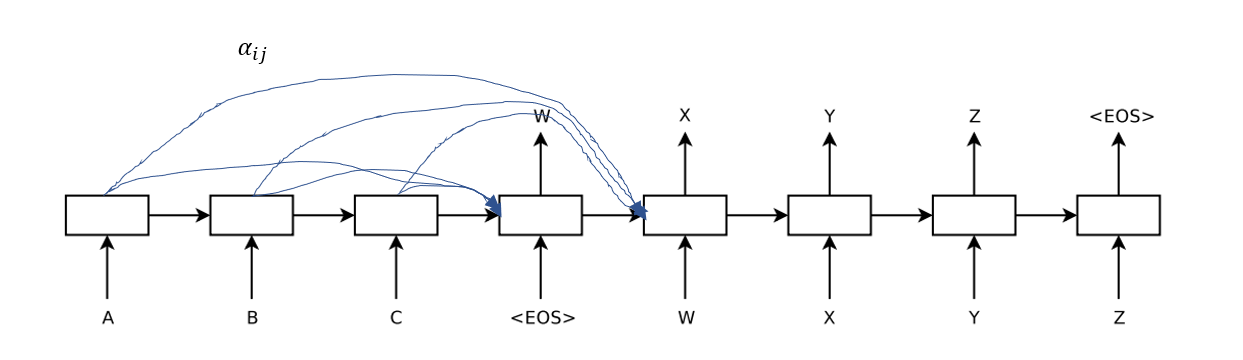
也就是说利用之前被我们抛弃的 Encoder 输出值，在预测每个单词的时候将其作为额外信息加入到解码器中，并赋予一定的权重 \(\alpha_{ij}\)，这样的结构使得在预测每个词的时候，关联词可以占有更高的权重，即赋予更高的注意力。

当然，Bahdanau 在关于 Attention 的论文中不只是这么简单的改进，但我认为上述描述是理解注意力机制比较简单的方式，接下来我们将更详细的讨论这一机制的演化过程。