LLM 推理加速技术原理 —— GPTQ 量化技术演进

GPTQ 是目前（2023-2024）在大模型量化领域应用得比较成熟的技术之一，本文将详细分析这种算法的演化过程，以便能够更好地理解其原理。

最优脑损伤（OBD）

OBD 的基本思想是以模型训练损失为目标函数，迭代地选择剪枝参数使目标函数最小化。具体来说，设模型的权重为 \(W\)，损失函数为 \(f\)，则在当前权重下，模型的训练损失为 \(L = L(W)\)。

模型剪枝实际上就是将 \(W\) 的某个值调整为 0，对损失函数进行泰勒展开可以估计权重调整造成的影响，对 \(L(W)\) 进行泰勒展开，得到

\[\begin{aligned} &L(W + \delta W) = L(W) + \left(\frac{\partial L}{\partial W}\right)^\top \delta W + \frac{1}{2} \delta W^\top H \delta W + \mathcal{O}(\delta W^3)\\ \Rightarrow & \delta L = \left(\frac{\partial L}{\partial W}\right)^\top \delta W + \frac{1}{2} \delta W^\top H \delta W + \mathcal{O}(\delta W^3) \end{aligned}\qquad (1)\]

其中 \(H\) 是 Hessian 矩阵。这里的 \(\delta L\) 就是剪枝后损失的变化量，显然 \(\delta L\) 越小越好，因此我们的目标就是找到一个 \(\delta W\)，使得 \(\delta L\) 最小。

一个训练好的神经网络模型，其损失一般都处于权重空间中的局部极小值，因此可以认为 \(\frac{\partial f}{\partial W} = 0\)，因此式中的第一项可以忽略。另外再忽略高阶项，则上式可以简化为

\[\delta L = \frac{1}{2} \delta W^\top H \delta W \qquad\qquad (2)\]

接下来我们需要介绍 OBD 的一个重要假设，为了进一步简化问题，OBD 认为 Hessian 矩阵是一个对角矩阵，其含义是，同时剪枝多个权重参数对模型精度造成的影响，等于单独剪枝每个权重对模型造成影响之和。也就是说

\[\delta L = \frac{1}{2} \sum_i \delta w_i^2 h_{ii}\]

这样一来，最终需要求解的问题就成了

\[i = \arg\min_i \frac{1}{2} \delta w_i^2 h_{ii}\]

其中 \(i\) 就是需要剪枝的权重参数在 \(W\) 中的索引。

最优脑手术（OBS）

OBS 受到 OBD 关于减小模型剪枝对损失函数影响的启发，但是不同意 OBD 的假设，认为权重剪枝之间是有关联的，所以不能简单地将 Hessian 矩阵假设为对角矩阵。于是从 (2) 式出发进行分析

\[\delta L = \frac{1}{2} \delta W^\top H \delta W \qquad\qquad (2)\]

假设对第 \(q\) 个参数进行剪枝，即 \(\delta w_q + w_q = 0\)，于是这里就变成了带约束的凸优化问题

\[\begin{aligned} &\arg\min_q \frac{1}{2} \delta W^\top H \delta W \\ &s.t.\quad \delta w_q + w_q = 0 \end{aligned}\]

其中的约束条件可以写成更一般的形式 \(\mathbf{e}_q^\top \delta W + w_q = 0\)，这里的 \(\mathbf{e}_q\) 是第 \(q\) 个值为 1 的单位向量。对于上述问题，可以使用拉格朗日乘子法来求解，定义拉格朗日函数

\[\mathcal{L} = \frac{1}{2} \delta W^\top H \delta W + \lambda (\mathbf{e}_q^\top \delta W + w_q)\]

对 \(\delta W, \lambda\) 求导，并设置为 0

\[\begin{aligned} \delta W^\top H + \lambda \mathbf{e}_q^\top = 0\\ \mathbf{e}_q^\top \delta W + w_q = 0 \end{aligned}\]

然后做如下变换

1: 对一个方程乘以 \(H^{-1}\)， 交换第二个方程的 \(\delta W\) 和 \(\mathbf{e}_q\)

\[\begin{aligned} \delta W^\top H H^{-1} + \lambda \mathbf{e}_q^\top H^{-1} = 0\\ \delta W^\top \mathbf{e}_q + w_q = 0 \end{aligned}\]

2: 第二个方程乘以 \(\mathbf{e}_q\)

\[\begin{aligned} \delta W^\top \mathbf{e}_q + \lambda \mathbf{e}_q^\top H^{-1} \mathbf{e}_q = 0\\ \delta W^\top \mathbf{e}_q + w_q = 0 \end{aligned}\]

3: 注意到 \(\mathbf{e}_q^\top H^{-1} \mathbf{e}_q = [H^{-1}]_{qq}\) ， 并将第二个方程带入第一个方程，得到

\[-w_q + \lambda [H^{-1}]_{qq}= 0\\\]

4: 解得

\[\lambda = \frac{w_q}{[H^{-1}]_{qq}}\]

5: 将 \(\lambda\) 带入第一个方程，解得

\[\delta W^\top = - \frac{w_q}{[H^{-1}]_{qq}} \mathbf{e}_q^\top H^{-1} =- \frac{w_q}{[H^{-1}]_{qq}} H^{-1}_{:,q} \qquad \qquad (3)\]

其中 \(H^{-1}_{:,q}\) 表示 \(H^{-1}\) 的第 \(q\) 列， 获得 \(\delta W \) 之后，将其带入 (2) 式

\[\begin{aligned} \delta L_q &= \frac{1}{2} \left(- \frac{w_q}{[H^{-1}]_{qq}} \mathbf{e}_q^\top H^{-1}\right) H \left(- \frac{w_q}{[H^{-1}]_{qq}} \mathbf{e}_q^\top H^{-1}\right)^\top\\ &= \frac{1}{2} \left(\frac{w_q}{[H^{-1}]_{qq}}\right)^2 \mathbf{e}_q^\top H^{-1} H (H^{-1})^\top \mathbf{e}_q\\ &= \frac 1 2 \left(\frac{w_q}{[H^{-1}]_{qq}}\right)^2 [H^{-1}]_{qq}\\ &= \frac 1 2 \frac{w_q^2}{[H^{-1}]_{qq}} \end{aligned}\]

于是可以解得 \(q\)

\[q = \arg\min_{q} \frac{w_q^2}{[H^{-1}]_{qq}} \qquad \qquad (4)\]

使用公式 (4) 可以找到当前最优的剪枝参数，然后再使用公式 (3) 计算所有权重的修正量，这就完成了一次迭代，交替应用 (3)(4)，即可不断找到需要剪枝的权重参数，直到达到剪枝的目标。

最优脑压缩（OBC）

OBS 的计算复杂度分析

OBS 在每次迭代中，都涉及到计算 Hessian 矩阵的逆矩阵，设权重参数总量为 \(d\)，则计算 Hessian 矩阵的逆矩阵的时间复杂度为 \(O(d^3)\)，且每次迭代都需要计算一次，因此 OBS 的时间复杂度为 \(O(d^4)\)。显然对于动则上百万甚至上亿参数的模型来说，这种方式的计算量是非常巨大的。

Row-wise 权重剪枝算法

OBC 原论文首先定义了 layerwise 的模型剪枝问题，也就是说，针对每一层，定义剪枝损失

\[\delta L(f(X, W), f(X, \hat{W}))\]

其中 \(f\) 表示某层的前向函数，\(W, \hat{W}\) 分别表示原始权重和剪枝后的权重矩阵，\(X\) 表示矩阵形式的输入。更具体的说，对于线性层或者卷积层，前向传播函数可以表示为权重和输入矩阵相乘的形式 \(f(X, W) = W X\)，再考虑将 \(\delta L\) 定义为平方损失函数，于是寻找最优压缩方案就变成了如下优化问题

\[\arg\min_{\hat{W}} \mid\mid WX - \hat{W} X\mid\mid^2\]

更进一步，若将权重矩阵按行分解，则剪枝损失又可以表示为按行求和的形式

\[\delta L = \sum_{i=1}^{d_{row}} \mid\mid W_{i,:} X - \hat{W}_{i,:} X\mid\mid^2\]

设 \(\delta L_i = \mid\mid W_{i,:} X - \hat{W}_{i,:} X\mid\mid^2\)，则 \(\delta L = \sum_{i=1}^{d_{row}} \delta L_i\)，并且有

\[\delta L_i = \mid\mid W_{i,:} X - \hat{W}_{i,:} X\mid\mid^2 = \sum_{k = 1}^N \left( \sum_{j=1}^{d_{col}} (w_{ij} - \hat{w}_{ij}) x_{jk} \right)^2\]

其中 \(N\) 表示 \(X\) 的列数，\(d_{col}\) 表示 \(X\) 的行数或者 \(W\) 的列数。

由于每次迭代我们都只对某一行中的一个权重进行剪枝，也就是说只影响一行的剪枝损失，所以在每次迭代过程中可以认为 \(\delta L = \delta L_i\)，其中 \(i\) 就是被剪枝权重所在的行索引。基于这样的事实，我们可以推导出 Hessian 矩阵为

\[\begin{aligned} H_{pq} &= \frac{\partial^2 \delta L_i}{\partial w_{ip} \partial w_{iq}} \\ &= \frac{\partial}{\partial w_{ip}} \sum_{k = 1}^N 2\left( \sum_{j=1}^{d_{col}} (w_{ij} - \hat{w}_{ij}) x_{jk} \right) \frac{\partial}{\partial w_{iq}} \sum_{j=1}^{d_{col}} (w_{ij} - \hat{w}_{ij}) x_{jk} \\ &= \frac{\partial}{\partial w_{ip}} \sum_{k = 1}^N 2\left( \sum_{j=1}^{d_{col}} (w_{ij} - \hat{w}_{ij}) x_{jk} \right) x_{qk} \\ &= 2\sum_{k=1}^N x_{pk} x_{qk} \end{aligned}\]

写成矩阵形式为

\[H = 2 X X^\top \qquad \qquad (5)\]

注意这是对第 \(i\) 行权重进行剪枝时的 Hessian 矩阵，让我们用 \(H^{(i)}\) 来表示，虽然对于每一行来说，初始时刻的 Hessian 矩阵都是相同的，但随着剪枝过程的进行，每一行相关的 Hessian 矩阵都会发生不同的变化。具体来说，Hessian 矩阵是一个仅与 \(X\) 相关的矩阵，当一次迭代对第 \(q\) 个权重剪枝后，\(X\) 的第 \(q\) 行就没有用了，下次迭代只需要从 \(H^{(i)}\) 中删除第 \(q\) 行和第 \(q\) 列即可，这种方式也节省了每次构造 \(H^{(i)}\) 的时间。

另一方面，每次迭代还需要计算 Hessian 逆矩阵，这是一个 \(O(d_{col}^3)\) 复杂度的操作，不过仍然有方法可以简化，设 \(H_F^{-1}\) 表示中间过程的 \(H^{-1}\)，其中 \(F\) 表示未量化的权重索引集合，\(H_{F/q}^{-1}\) 表示 \(H_F^{-1}\) 去掉第 \(q\) 行和第 \(q\) 列后的矩阵，那么有以下公式成立

\[H^{-1}_{F/q} = \left(H_F^{-1} - \frac{1}{[H_F^{-1}]_{qq}} [H_F^{-1}]_{:,q} [H_F^{-1}]_{q,:}\right)_{-q} \qquad \qquad (6)\]

关于这个公式的证明可以参考原论文，这里就不赘述了。通过这个公式，可以将每次迭代的 Hessian 逆矩阵的计算复杂度降低到 \(O(d_{col}^2)\)。

通过以上的讨论，我们可以暂时总结一下优化后的 OBS 算法步骤：

1. 根据公式 (5) 计算初始 Hessian 矩阵 \(H^{(i)}\)，并为权重矩阵的每一行复制一份；
2. 遍历每一行，根据公式 (4) 计算出最佳权重索引 \(q_i\)，其中 \(i\) 为所在行索引，对应的 Hessian 矩阵是 \(H^{(i)}\)；
3. 应用公式 (3) 计算当前行的权重修正量，然后更新权重矩阵；
4. 更新第 \(i\) 行的 Hessian 矩阵 \(H^{(i)}\)，并根据公式 (6) 更新 Hessian 逆矩阵；
5. 重复步骤 2-4，直到达到剪枝目标。

显然，上述过程每次迭代都需要应用 \(d_{row}\) 次公式 (4)，然后挑选最佳的 \(q_i\)。举个例子来说，假如第一次迭代选择了第 10 行，第二次迭代选择了第 5 行，但事实上，由于每一次迭代只影响当前行的 Hessian 矩阵，不同行之间的 Hessian 矩阵计算是相互独立的，也就是说，即便第一次迭代选择了第 5 行，也不会对第 10 行的索引计算造成影响，所以不同行之间的迭代是可以并行的。

从 OBS 到 OBQ

剪枝和量化都涉及到对权重值的修改，只不过剪枝是直接将权重设置为 0，而量化则是降低权重值的数值精度，比如将 fp32 数值变成 fp16，int8，int4 等，因此 OBS 的思想可以很自然的应用到量化上来，这种方法也被称为 OBQ (Optimal Brain Quantization)，而为了兼顾剪枝和量化，论文的标题就叫 OBC (Optimal Brain Compression)。

对于 OBQ 方法，我们仍然从公式 (2) 出发

\[\delta L = \frac{1}{2} \delta W^\top H \delta W \qquad\qquad (2)\]

在 OBS 中，对应的约束条件为 \(\delta w_q + w_q = 0\)，也就是说，索引为 \(q\) 的权重修改量为 \(-w_q\)，而在量化条件下，情况要复杂一点，根据 Google量化白皮书，量化实际上就是将浮点数权重转换为整数

\[\begin{aligned} w_Q &= clamp(0, N - 1, round(\frac{w}{scale}) + z) \end{aligned}\]

其中 \(scale\) 表示缩放系数，\(z\) 表示零点偏移，\(N\) 表示最大整数值。以 \(scale=0.09655, z = 8, N = 16\) 为例，量化函数图像如下

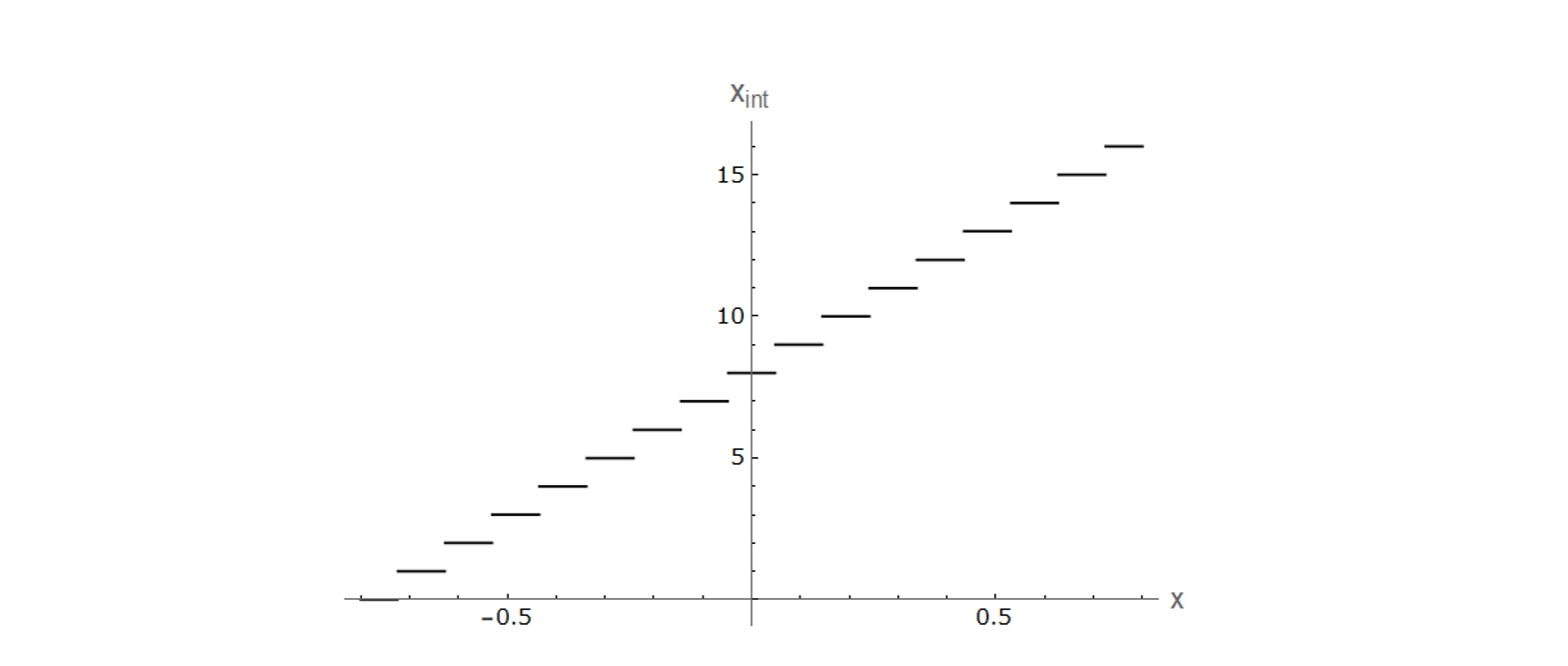
可以看到，该函数将浮点数权重分阶段地映射到了整数值上。一个训练好的模型，对所有权重值应用量化变换，并保存好相应的 \(scale, z, N\) 等参数，这就是经典的量化过程。

与量化过程对应的还有一个逆量化操作可以恢复原先的精度类型

\[w_{Q_f} = scale \times (w_Q - z)\]

因此，量化后的权重实际上存在两种等价的表示形式，第一种是通过量化函数变换到的整数空间，第二种是通过逆量化函数变换到的浮点数空间。显然在浮点数空间中，权重参数是一个个的离散点，这些点就构成了一个量化网格(quantization grid)。对于 OBQ 来说，每量化一个权重值，需要调整剩余权重来最小化量化损失，但是我们不能直接在整数空间上调整（因为剩余权重都是浮点数），而应该在浮点数空间上调整，定义函数 \(quant\) 先对权重进行量化，再逆量化，就得到浮点数空间上的量化值

\[quant(w) = scale \times (clamp(0, N - 1, round(\frac{w}{scale}) + z) - z)\]

于是剪枝操作中的约束条件 \(\delta w_q + w_q = 0\) 在这里就变成了 \(\delta w_q + w_q = quant(w_q)\)。再次使用拉格朗日乘子法求解公式 (2) 的最小化问题，可以得到

\[q = \arg\min_{q} \frac{(quant(w_q) - w_q)^2}{[H^{-1}]_{qq}} \qquad \qquad (7)\] \[\delta W = - \frac{w_q - quant(w_q)}{[H^{-1}]_{qq}} (H^{-1}_{:,q})^\top \qquad \qquad (8)\]

这里的 \(\delta W\) 表示一行权重的修正量，初始大小为 \(1\times d_{col}\)。交替使用公式 (7)(8) 就得到了量化版本的 OBC 算法 OBQ。

GPTQ

按索引顺序量化

OBQ 采用 row-wise 的权重量化方法，将 Hessian 矩阵求逆的复杂度降低到了 \(O(d_{col}^2)\)，并且一个权重矩阵总的参数量为 \(d_{row} \times d_{col}\)，因此总体来说 OBQ 的时间复杂度为 \(O(d_{row} \times d_{col}^3)\)。虽然相对于 OBS 的 \(O((d_{row}\times d_{col})^4)\) 有了相当大的改进，但对于大模型来说，OBQ 仍然是一个非常耗时的操作。

GPTQ 提出了两点改进来提高 OBQ 的量化效率，首先是将每一行的量化权重选择方式从贪心策略改成按索引顺序选择，其次是将权重更新方式修改为批量更新，我们将会说明，后者实际上依赖于前者。

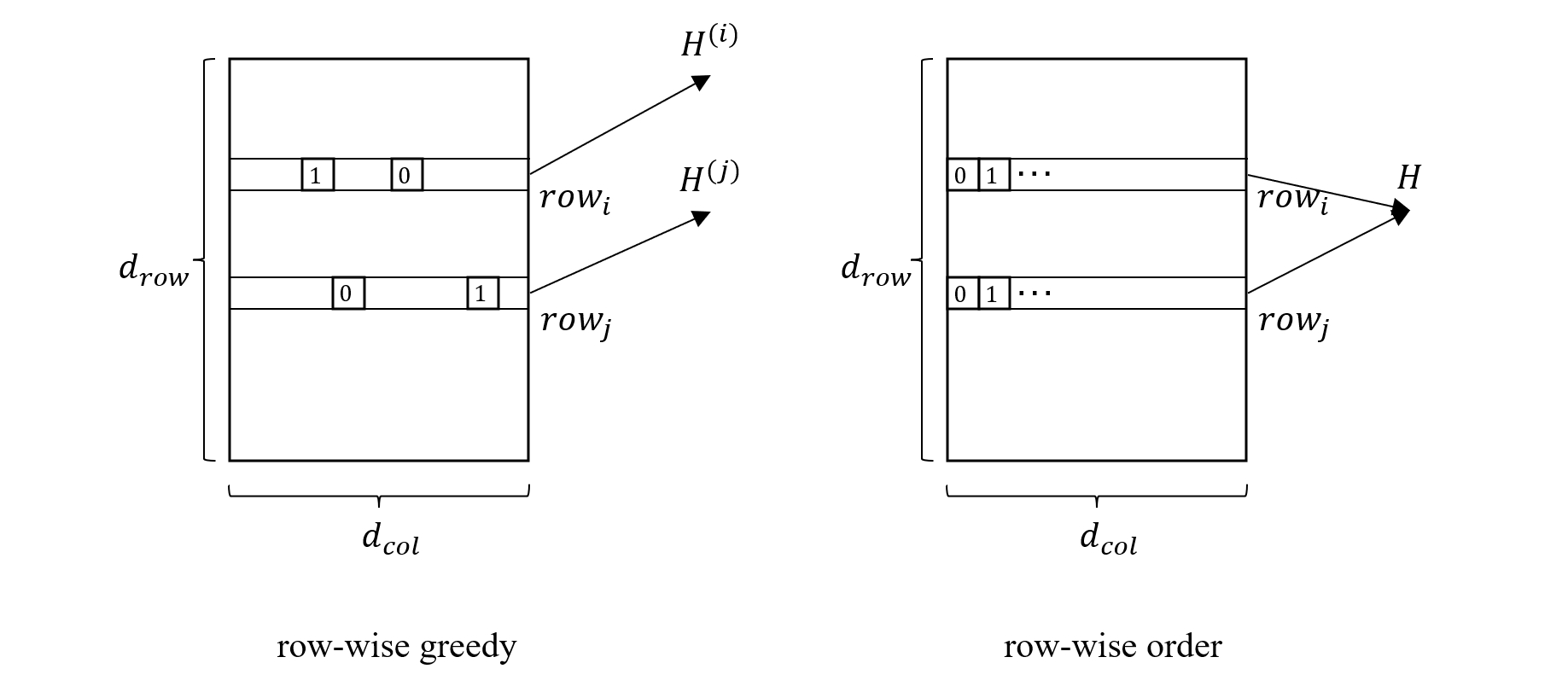
在 OBQ 算法中，每次迭代都需要使用公式 (7) 来计算当前行的最佳权重，GPTQ 作者认为这种贪心策略虽然能达很高的准确性，但相对于任意顺序的权重选择方式来说提升效果并不是很大，如果让所有行都按一样的顺序来量化权重，则可以极大的简化量化过程。

根据前面的公式（5）

\[H = 2 X X^\top \qquad \qquad (5)\]

可以看到，对于权重矩阵的每一行来说，其初始 Hessian 矩阵只与输入矩阵 \(X\) 相关，因此都是相同的。在 OBQ 中，每一行权重的优化顺序都可能不一样，因此每一行对应的 Hessian 矩阵也都会变得不一样，需要单独保存。而当所有行都按一样的顺序来量化权重时，每一行对应的 Hessian 矩阵都是相同的，因此逆矩阵也相同，这就意味着只需要计算 \(d_{col}\) 次逆矩阵，而不是 \(d_{col}\times d_{row}\) 次，这样一来总的时间复杂度就降低到了 \(O(d_{col}^3)\)，同时也省略了公式 (7) 寻找最优权重的计算过程。

由于每行的权重量化是按 0 到 \(d_{col}\) 的顺序进行的，那么在量化第 \(q\) 个权重时，用到的 Hessian 逆矩阵可以表示为 \([H_{q:, q:}]^{-1}\)，于是权重调整量计算公式 (8) 可以做出相应的修改

\[\delta W = - \frac{w_q - quant(w_q)}{[H_{q:, q:}]^{-1}_{0,0}} ([H_{q:, q:}]^{-1}_{:,0})^\top \qquad \qquad (9)\]

同时 Hessian 逆矩阵的更新公式 (6) 也可以重写为

\[[H_{q:,q:}]^{-1} = \left([H_{q-1:,q-1:}]^{-1} - \frac{1}{[H_{q-1:,q-1:}]^{-1}_{00}} [H_{q-1:,q-1:}]^{-1}_{:,0} [H_{q-1:,q-1:}]^{-1}_{0,:}\right)_{1:,1:} \qquad \qquad (10)\]

再考虑到所有行都是按照一样的顺序来量化权重，那么一次迭代就可以量化同一列的所有行，于是我们可以构造向量化的权重调整公式

\[\delta W = -\frac{W_{:, q} - quant(W_{:, q})}{[H_{q:, q:}]^{-1}_{0,0}} ([H_{q:, q:}]^{-1}_{:,0})^\top \qquad \qquad (11)\]

其中 \(W_{:, q}\) 表示权重矩阵的第 \(q\) 列，大小为 \(d_{row}\times 1\)。

Cholesky 分解

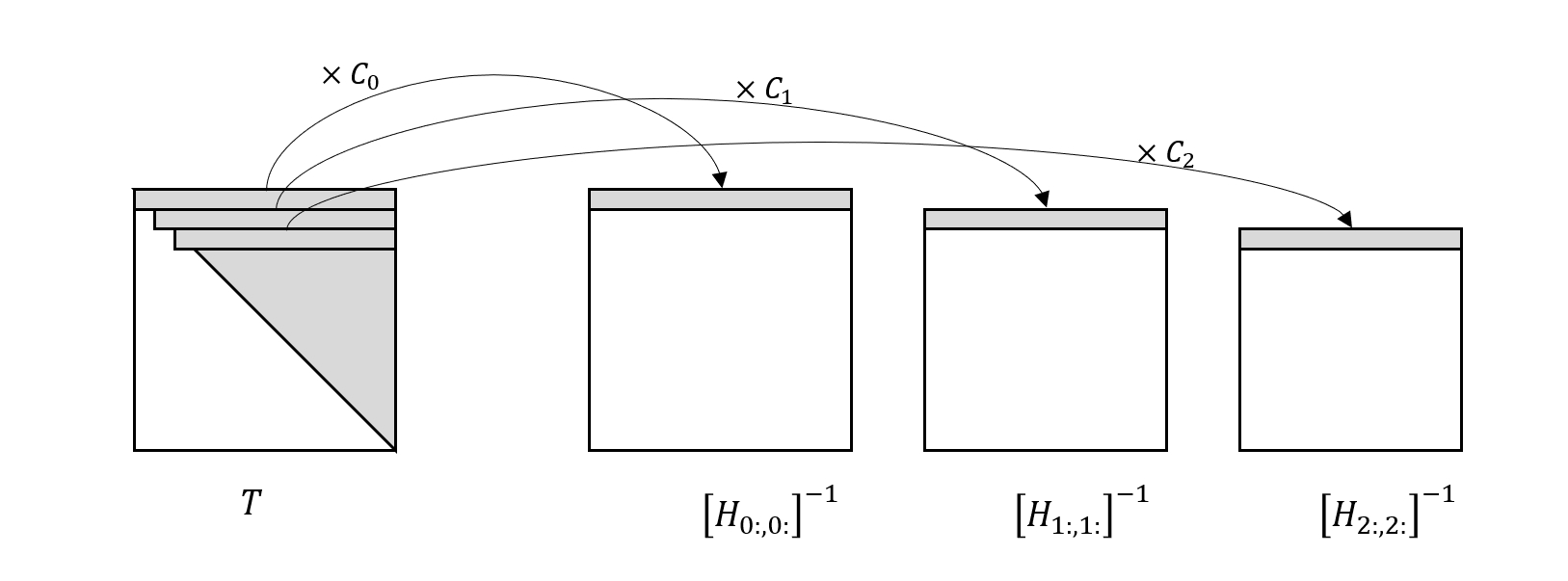
GPTQ 还应用 Cholesky 分解来解决 \(H\) 逆矩阵计算的数值稳定性问题。原作者在实验过程中注意到在大规模参数矩阵上重复的应用公式 (10) 几乎总是会产生非正定的 Hessian 逆矩阵，原因可能是由于数值误差的累积导致的，从而导致量化过程失败。为了解决这个问题，作者对初始的 \(H^{-1}\) 使用 Cholesky 分解，得到一个上三角矩阵 \(T\)，这个 \(T\) 非常的有意思，它的每一行刚好就等于连续应用公式 (10) 得到的矩阵序列的第一行乘以一个常数，也就是说

\[C_q T_{q, q:} = [H_{q:, q:}]^{-1}_{0,:}\]

用图示的方式表示如下

再考虑公式 (11)，将其计算过程可视化如下图

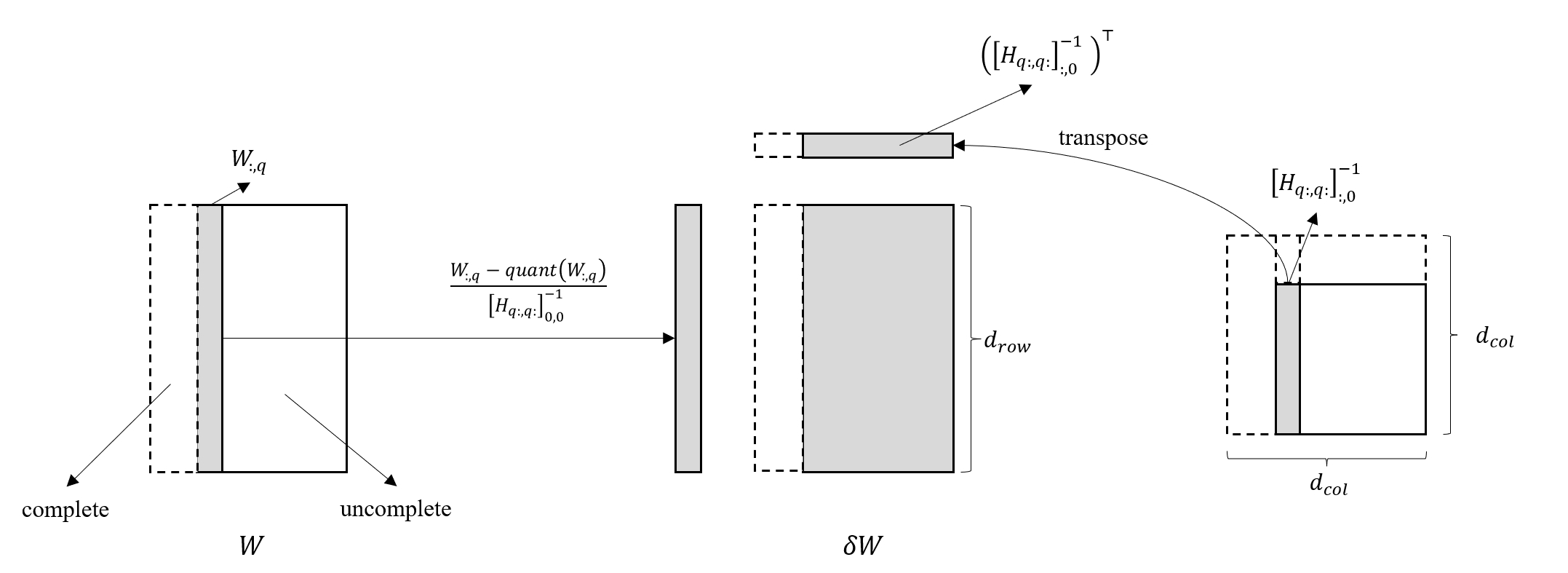
可以看到，在量化第 \(q\) 列权重时，仅用到了当前 Hessian 逆矩阵 0 列的元素，即 \([H_{q:, q:}]^{-1}_{:, 0}\)，而由于 Hessian 矩阵是对称的，因此等于 \([H_{q:, q:}]^{-1}_{0, :}\)，也等于 \(C_q T_{q,q:}\)。

通过以上分析可以发现，不必应用公式 (10)，仅仅利用 Cholesky 分解得到的 \(T\) 矩阵，就可以得到量化过程中与 Hessian 逆矩阵相关的所有信息。利用 \(T\) 与 Hessian 逆矩阵的关系，我们可以将公式 (11) 修改成使用 \(T\) 的表示形式

\[\delta W = -\frac{W_{:, q} - quant(W_{:, q})}{C_q T_{qq}} C_q T_{q,q:} \qquad \qquad (12)\]

注意 \(T\) 与 Hessian 逆矩阵之间相差的常数在上式中抵消掉了。

批量量化

前面已经假设了，权重量化顺序对最终量化效果影响不是很大，那么同时量化多个列的权重实际上也是包含在这个假设之内的，因此 GPTQ 进一步给出了批量量化方法，具体来说就是对公式 (12) 的批量化，如下图所示

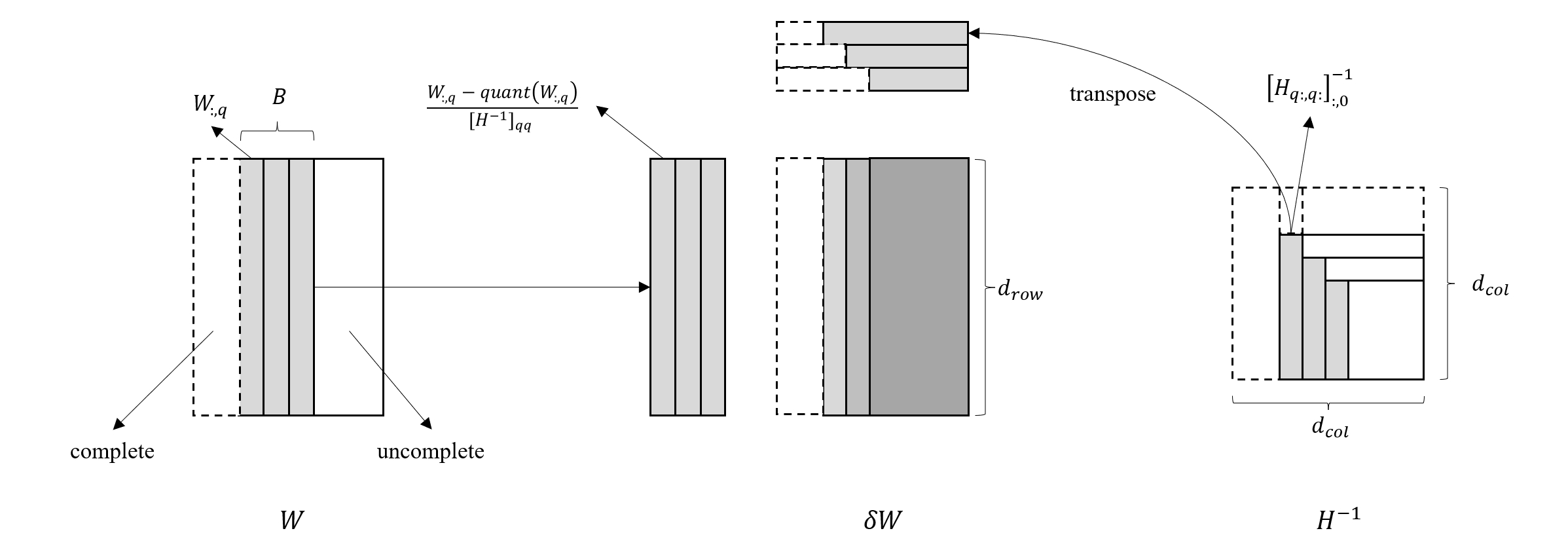
这个过程的难点在于每量化一行，对应的 Hessian 逆矩阵的尺寸就会减小一，因此在批量计算中，对应的 \(T_{q,q:}\) 向量是阶梯型减小的，这种结构不适合直接使用矩阵乘法。为了解决这个问题，我们考虑如下图所示的分解

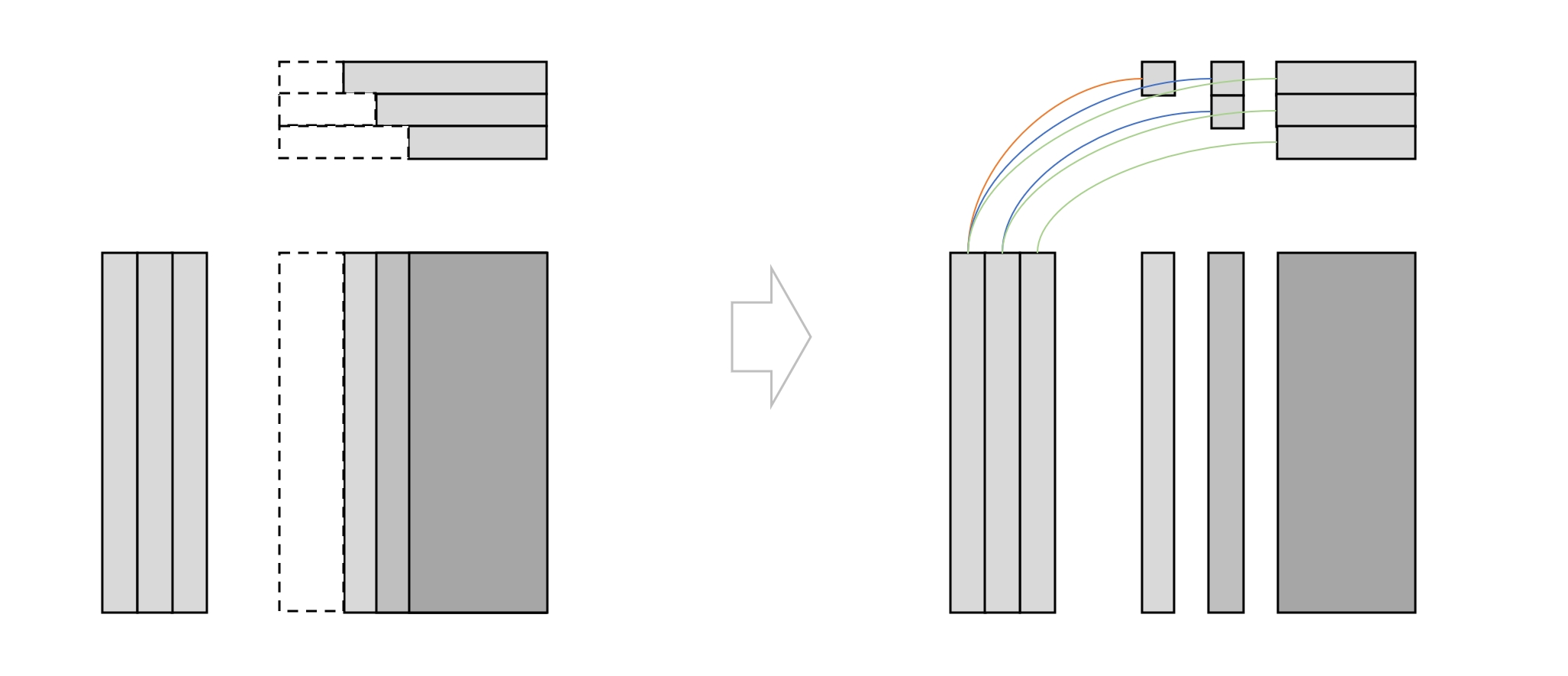
分解之后，前 \(B-1\) 次迭代用于计算相关列的权重调整量，最后一次迭代用于计算剩余列的权重调整量，这样就很大程度上减少了读取权重矩阵的次数，从而提高了计算效率。

总结

以上就是关于 GPTQ 量化技术的完整演化过程，总的来说，OBD 开创了利用剪枝损失的二阶信息来挑选最佳权重的思路，OBS 在此基础之上构造凸优化问题求解权重修正量，OBQ 则将 OBS 的思想应用到了模型量化过程，最后，GPTQ 提出若干优化措施加速了量化过程，使得量化技术在大规模模型上也能得到有效的应用。

参考

• LeCun, Yann, John Denker, and Sara Solla. “Optimal brain damage.” Advances in neural information processing systems 2 (1989).

• Hassibi, Babak, David G. Stork, and Gregory J. Wolff. “Optimal brain surgeon and general network pruning.” IEEE international conference on neural networks. IEEE, 1993.

• Frantar, Elias, and Dan Alistarh. “Optimal brain compression: A framework for accurate post-training quantization and pruning.” Advances in Neural Information Processing Systems 35 (2022): 4475-4488.

• Frantar, Elias, et al. “Gptq: Accurate post-training quantization for generative pre-trained transformers.” arXiv preprint arXiv:2210.17323 (2022).