LLM 推理加速技术 -- Flash Attention 的算子融合方法
本文来自于对 FlashAttention 论文的理解,对原论文省略的一部分数学过程做了展开讲解。
简单来说,Flash Attention 的核心思想是利用分块方法融合 softmax 和 matmul 来降低 HBM 访存次数从而提高效率。
标准 Attention 的访存复杂度分析
Attention 的计算公式如下:
\[O = softmax \left(\frac{QK^\top}{\sqrt{d}}\right)V\]其中 \(Q, K, V\in \mathbb{R}^{N\times d}\) 分别是 query, key, value, N 是输入序列的长度,d 是 head dimension,O 是 attention 的输出。
如果严格按照上式编写代码,则需要进行以下步骤:
- 计算 \(S = \frac{QK^\top}{\sqrt{d_k}}\),这一步需要从 HBM 中读取
Q, K,计算S,然后将S写回 HBM。访存复杂度为 \(\Theta(Nd + N^2)\),其中 \(Nd\) 是Q, K矩阵的大小,\(N^2\) 是S矩阵的大小。 - 计算 \(P = softmax(S)\),这一步需要从 HBM 中读取
S,计算P,然后将P写回 HBM,访存复杂度为 \(\Theta(N^2)\)。 - 计算 \(O = PV\),这一步需要从 HBM 中读取
P, V,再计算O,然后将O写回 HBM,访存复杂度为 \(\Theta(Nd + N^2)\)。
所以总的来说,标准的 Attention 计算的访存复杂度为 \(\Theta(Nd + N^2)\)。
分解 Softmax 计算
向量的 softmax
考虑一个维度为 \(B\) 的向量 \(x\in \mathbb{R}^B\),并且规定 \(\exp(x)\) 表示
\[\exp(x) = [e^{x_1}, e^{x_2}... , e^{x_B}]\]则 softmax 的计算公式如下
\[softmax(x) = \frac{\exp(x)}{\sum_{j=1}^B e^{x_j}}\]再定义 \(f(x) = \exp(x)\),且 \(l(x) = \sum_j\exp(x_j)\),于是可以将 softmax 重新写为
\[softmax(x) = \frac{f(x)}{l(x)}\]现在我们再考虑两个向量 \(x^{(1)}, x^{(2)}\),以及它们的拼接向量 \(x = [x^{(1)}, x^{(2)}]\)。为了简单起见,设 \(f_i = f(x^{(i)}), l_i = l(x^{(i)})\) 。则 \(x\) 的 softmax 可以写为
\[softmax(x) = \frac{[f_1, f_2]}{l_1+ l_2} = \left[\frac{f_1}{l_1} \times \frac{l_1}{l_1 + l_2} , \frac{f_2}{l_1 + l_2}\right]\]也就是说,假如我们事先不知道完整的 \(x\),而只有 \(x^{(1)}\),那么可以先计算 \(f_1\) 和 \(l_1\),当 \(x^{(2)}\) 准备好之后,再计算 \(f_2\) 和 \(l_2\),并对之前计算的 \(\frac{f_1}{l_1}\) 进行修正,从而得到最终的 \(softmax(x)\)。
矩阵的 softmax
下面我们再将问题推广到矩阵情况,设矩阵 \(X^{(1)}, X^{(2)}\),以及它们的拼接矩阵 \(X = [X^{(1)}, X^{(2)}]\),设 \(f_i = \exp(X^{(i)}), l_i = rowsum(\exp(X^{(i)}))\)。则
\[softmax(X^{(i)}) = \frac{f_i}{l_i}\]注意这里的除法被定义为矩阵的每一行除以对应位置上向量的元素,结果还是矩阵。对于 \(X\) 来说
\[softmax(X) = \left[\frac{f_1}{l_1 + l_2}, \frac{f_2}{l_1+l_2}\right] = \left[\frac{f_1}{l_1} \odot \frac{l_1}{l_1+ l_2}, \frac{f_2}{l_1+l_2}\right]\]其中 \((\odot)\) 符号在这里表示矩阵的每一行乘以对应行上向量的元素。
Attention 算子融合
以上介绍的分解方法对于单纯的 softmax 计算来说没什么用,但是它可以帮助我们将 softmax 与矩阵乘法进行融合,从而降低降低 IO 复杂度。
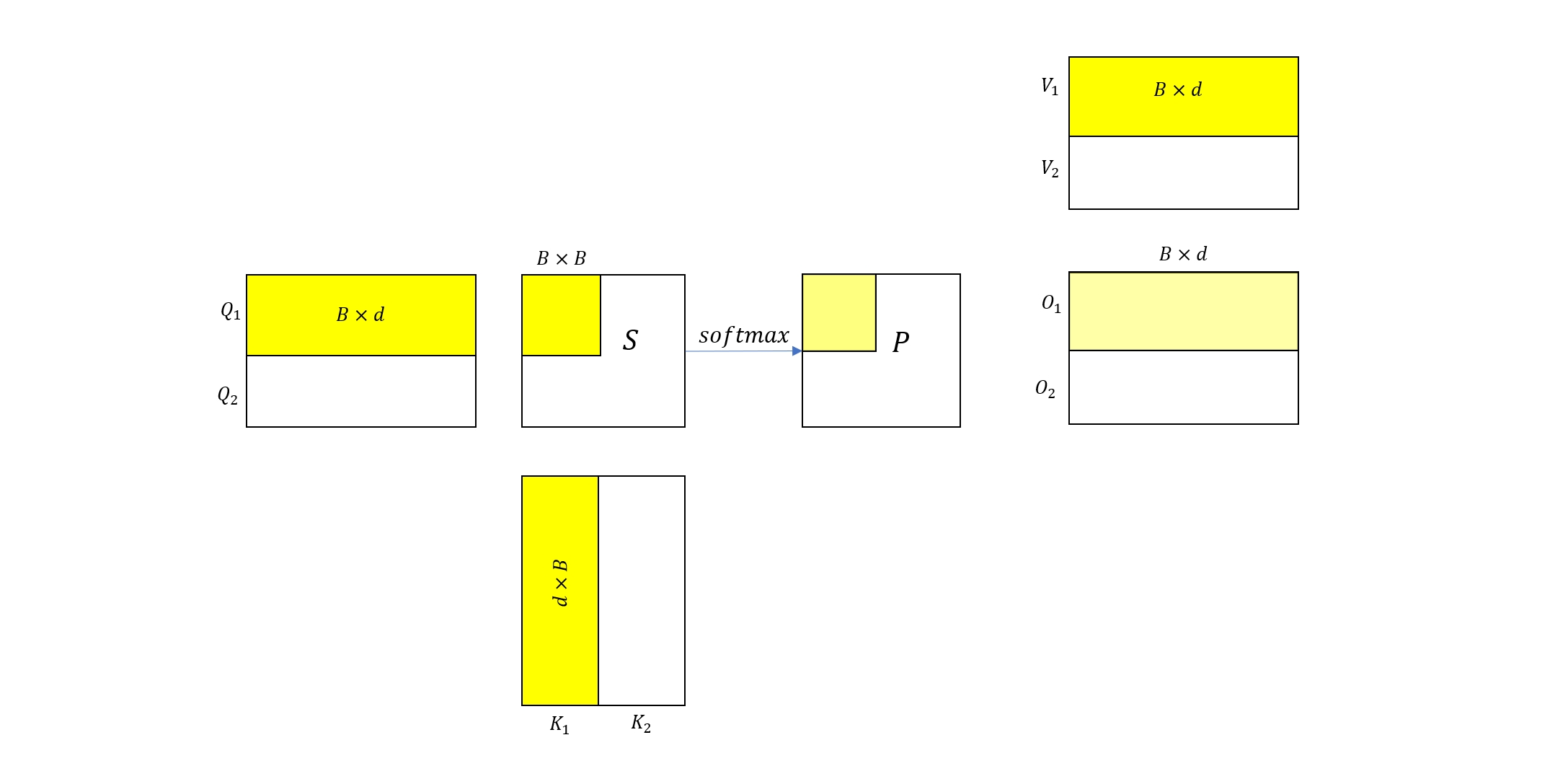
二分块情况
考虑上图所示的 Attention 计算过程,为了简化说明,我们将 Q, K, V 矩阵都分成两块,每块的大小都为 \(B\times d\)。首先考虑分块的计算过程,读取 \(Q_1, K_1 ,V_1\) 到 shared memory 中(假设矩阵分块足够小,能够被 sm 容纳),然后依次计算 \(S_{11}\) 和 \(P’{11}\) 以及 \(O’_1\)(注意这里 \(P’{11} \ne P_{11}, O’_1 \ne O_1\) 都不是最终结果,所以图中我们用浅黄色来表示),并将 \(O’_1\) 写回 HBM。
类似于上一节,我们做如下定义
\[f_{11} = \exp(S_{11}), \quad l_{11} = rowsum(\exp(S_{11}))\]于是 \(O’_1\) 可以改写为
\[O'_1 = \frac{f_{11}}{l_{11}} V_1\]接下来考虑整体的 Attention 计算 \(\begin{aligned} S &= \frac{Q K}{\sqrt{d}} \\ P &= softmax(S)\\ O &= P V \end{aligned}\)
其中 \(O = [O_1, O_2]^\top\),\(O_1 = P_{11} V_1 + P_{12}V_2\),而 \(P_{11}, P_{12}\) 来自于
\[[P_{11}, P_{12}] = softmax([S_{11}, S_{12}])\]然后我们再定义
\[\begin{aligned} f_{11} &= \exp(S_{11}) \\ f_{12} &= \exp(S_{12}) \\ l_{11} &= rowsum(\exp(S_{11})) \\ l_{12} &= rowsum(\exp(S_{12})) \end{aligned}\]根据上一节的推导,我们可以得出
\[[P_{11}, P_{12}] = \left[\frac{f_{11}}{l_{11}}\odot \frac{l_{11}}{l_{11} + l_{12}}, \frac{f_{12}}{l_{11} + l_{12}} \right]\]然后将 \(P_1, P_2\) 代入到 \(O_1\) 的计算公式,可以得到
\[\begin{aligned} O_1 &= \frac{f_{11}}{l_{11}}\odot \frac{l_{11}}{l_{11} + l_{12}} V_1 + \frac{f_{12}}{l_{11} + l_{12}} V_2 \\ &= \frac{f_{11}}{l_{11}}V_1\odot \frac{l_{11}}{l_{11} + l_{12}} + \frac{f_{12}}{l_{11} + l_{12}} V_2 \end{aligned}\]再考虑到我们前面推导的 \(O’1 = \frac{f{11}}{l_{11}}V_1\),于是可以得出 \(O_1\) 和 \(O’_1\) 之间的关系
\[O_1 = O'_1 \odot \frac{l_{11}}{l_{11} + l_{12}} + \frac{f_{12}}{l_{11} + l_{12}} V_2\]同理,还有 \(O_2\) 与 \(O’_2\) 之间的关系
\[O_2 = O'_2 \odot \frac{l_{21}}{l_{21} + l_{22}} + \frac{f_{22}}{l_{21} + l_{22}} V_2\]多分块情况
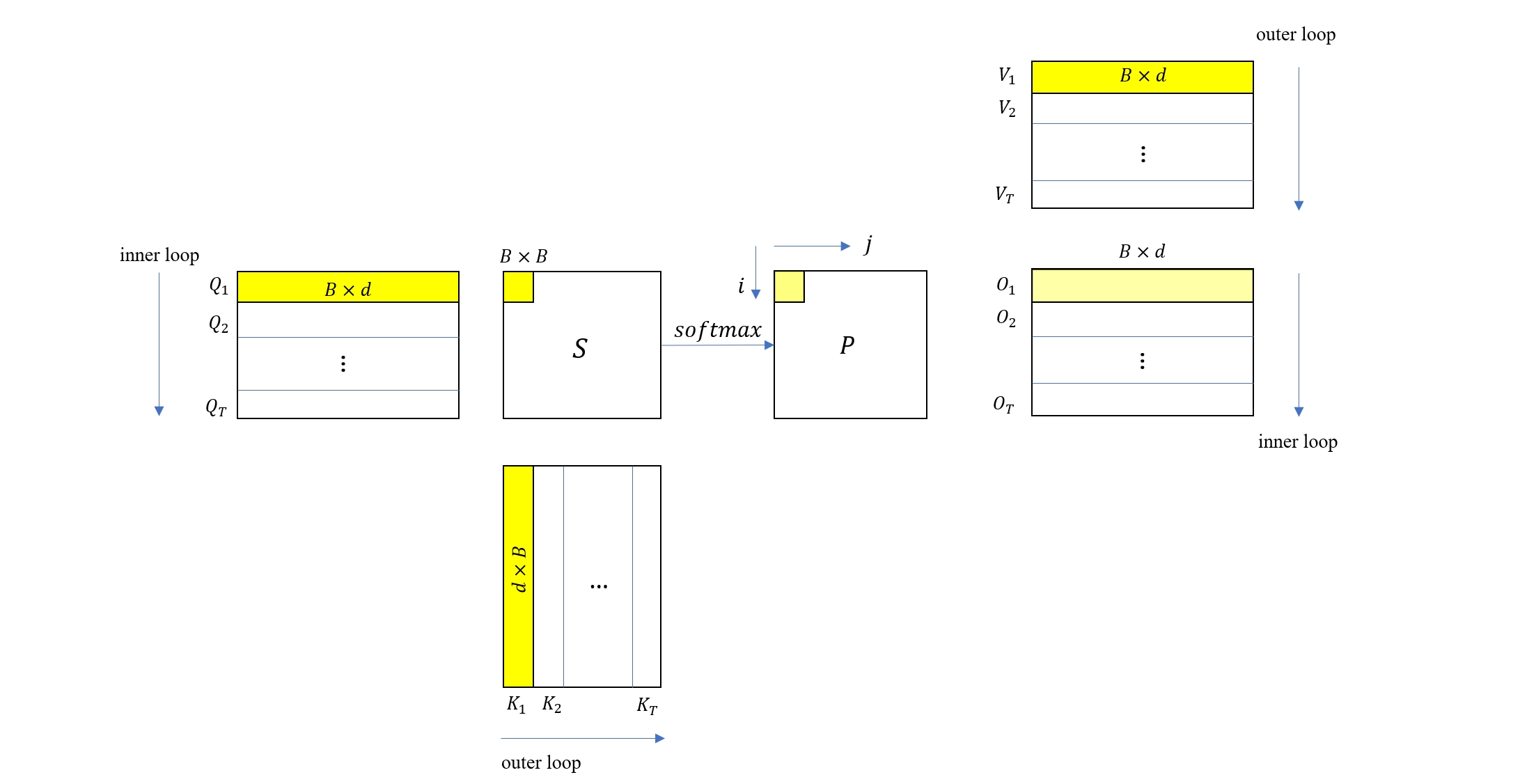
下面我们把之前推导的二分块推广到多分块情况,如上图所示,Q, K, V 被分块为 \(Q_{1…T}, K_{1…T}, V_{1…T}\),每个分块的大小都为 \(B\times d\)。
为了计算所有的 O 分块,这里使用双层循环来遍历 Q,K,V 的所有分块,其中外层循环遍历 K, V 的分块,内层循环遍历 Q, O 的分块。在外层循环的第一次迭代中,内层循环依次计算出了 \(O_1, O_2, … O_T\)(注意这里的结果都不是最终结果)。
外循环的第二次迭代,就可以按上一节讨论的公式来修正,即
\[O_j := O_j \odot \frac{l_{j1}}{l_{j1} + l_{j2}} + \frac{f_{j2}}{l_{j1} + l_{j2}} V_2\]外循环的第三次迭代,继续修正
\[O_j := O_j \odot \frac{l_{j2}}{l_{j2} + l_{j3}} + \frac{f_{j3}}{l_{j2} + l_{j3}} V_3\]于是可以得出结论,对于外循环的第 \(i\) 次迭代,迭代格式为
\[O_j := O_j \odot \frac{l_{j,i-1}}{l_{j,i-1} + l_{ji}} + \frac{f_{ji}}{l_{j,i-1} + l_{ji}} V_i\]Attention 融合计算的访存量分析
根据上面的分析,Attention 融合计算需要分批次将 Q, K, V 的一部分数据从 HBM 载入到 SM 中,假设它的大小为 M,则每次计算从 Q, K, V 矩阵载入的访存复杂度都为 \(\Theta(M)\)。
从循环关系来看,外层循环次数为 \(\Theta(\frac{Nd}{M})\),而载入一次 \(K_i, V_i\) 后需要遍历所有的 \(Q_j, O_j\),所以每次外循环访存数据量都在 \(\Theta(Nd)\) 量级,于是总的访存量就为 \(\Theta(N^2d^2M^{-1})\)。
以一个比较典型的场景为例,假设 N = 1024, d = 64, M = 100kb,则标准 Attention 在 float16 数据精度下的访存量为 (1024 x 1024 + 1024 x 64) x 2 / 1024 kb = 2176kb,而在分块计算条件下这一值为 (1024 x 1024 x 64 x 64) / (100 x 1024) x 2 / 1024 kb = 81.92kb。虽然这里只是按渐进复杂度做的极为粗略的计算,也不难看出使用分块计算能极大的节省内存访问次数,从而提高 Attention 算术强度,由于在大多数硬件下 Attention 都是内存密集型的,也就是说其算术强度始终位于 Roofline 模型的左边部分,因此提高算术强度能直接提高硬件的利用率。
总结
本文对 Flash Attention 的算子融合过程进行分析,重点阐述了 mulmat 和 softmax 的融合计算方法,并从访存复杂度的角度解释了为什么 Flash Attention 会更快。