LLM 的困惑度指标定义及其计算

困惑度是评价语言模型生成质量的重要参考指标之一，本文将从概念到公式到代码全方位展示如何计算一个语言模型的困惑度，这将有助于我们在特定任务上定量地评估某个 LLM 的生成质量，以及模型量化后的质量损失。

离散型随机变量的概率质量函数以及累计分布函数

设一个离散型随机变量 \(X\) 的概率质量函数为 \(p(x)\)，也就是说对于任意的 \(x_i \in \mathcal{X}\)，\(P(X = x_i) = p(x_i)\)，其中 \(\mathcal{X}\) 是 \(X\) 的样本空间。那么 \(X\) 的累计分布函数 \(F_X(x)\) 定义为

或者反过来，如果已知 \(X\) 的累计分布函数 \(F_X(x)\)，则可以通过下面的公式计算 \(X\) 的概率质量函数

经验分布函数

经验分布函数是对真实概率累计分布函数在给定样本集上的估计，比如在样本集 \({x_i}_1^{n}\) 上，假设 \(x_1 < x_2 < … < x_n\)，则其经验分布函数被定义为

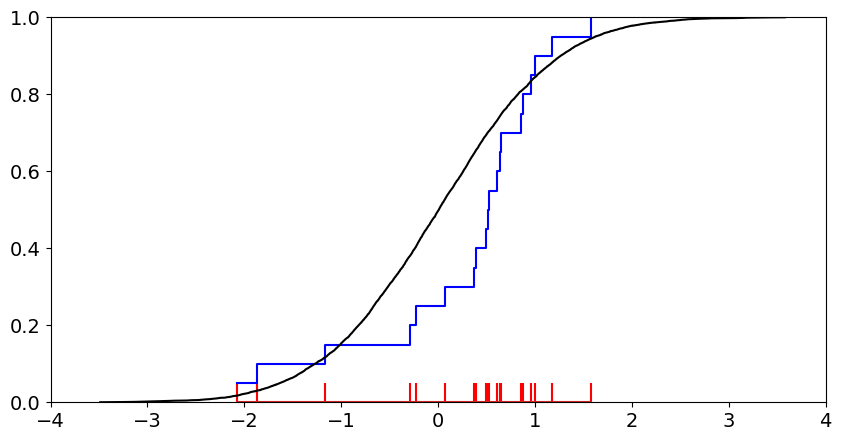
关于为什么上面这个简单的定义就能估计真实的概率分布，可以参考 Glivenko–Cantelli 定理，该定理证明了当 \(n \rightarrow \infty\) 时，经验分布函数一致收敛到真实分布。从直观的角度来讲，可以考虑下面这个例子，设在标准正态分布上采样多个样本，如下图所示的红色脉冲点，它的经验分布函数就是图中的蓝色折线，可以看到，蓝色折线与标准正态分布的累计分布函数（即黑色曲线）是相当接近的。

经验分布的概率质量函数

类似真实概率质量函数与累计分布函数之间的关系，经验分布的概率质量函数可以由上面定义的经验分布函数来计算，即

当然，有的文章会把上式表述成

其中 \({1\mid x = x_i}\) 是指示函数，当 \(x = x_i\) 时等于 1，否则等于 0。

信息量与信息熵

设随机变量 \(X\) 的概率质量函数为 \(p(X)\)，则 \(X=x\) 这个事件的信息量被定义为

当 log 函数的底数等于 2 时，上式的含义可以被认为是：使用二进制数据对 \(x\) 进行编码所需要的比特数。比如，当 \(p(x) = 1\) 时，不用对消息进行编码我们也知道 \(x\) 一定发生，它对应的信息量等于 0。而当 \(p(x) = 0.5\) 时，\(x\) 发生与不发生的概率各占一般，此时 \(I(x) = 1\)，也就是说我们需要 1 个比特来对 \(x\) 进行编码，可以用 0 表示不发生，1 表示发生。

信息熵则是随机变量的平均信息量，其定义为

其中 \(\mathcal{X}\) 是 \(X\) 的样本空间。由于在一个概率分布中，有的事件发生概率大，有的事件发生概率小，因此使用信息熵可以用来表示编码该分布中一个事件所需的平均比特数。

概率分布的困惑度

困惑度是在离散概率分布中采样不确定性的度量，困惑度越大，采样的不确定性就越高。这种定义看起来和熵的概念有一定的关系，事实上，对于一个离散随机变量 \(X\) 的概率分布 \(p\) 来说，它的困惑度正是由熵 \(H(p)\) 来决定的，其公式如下：

交叉熵

设两个定义在相同样本空间上的概率分布 \(p\) 和 \(q\)，并设 \(p\) 是真实的概率分布，\(q\) 是对 \(p\) 的近似。当使用 \(q\) 来衡量 \(X=x\) 的信息量（或者说编码长度）时，可以得到 \(I_q(x) = -\log_2 q(x)\)。但我们知道 \(X = x\) 的实际发生概率为 \(p(x)\)，于是使用 \(q\) 来衡量随机变量的平均信息量就等于

这个量就是 \(p,q\) 之间的交叉熵，可以看到，当 \(p = q\) 时，\(H(p, q) = H(p)\)。

概率模型的困惑度

概率模型是对真实概率分布的建模，因此概率模型的困惑度可以看作是对概率分布困惑度的近似，当概率模型能够完美地拟合真实概率分布时，概率模型的困惑度就等于真实概率分布的困惑度。从这个意义上来看，我们可以使用概率模型与概率分布之间的交叉熵来定义概率模型的困惑度，即

由于真实概率分布未知，所以这里我们使用经验分布来代替真实概率分布，使用前面推导的结论，对于一个样本空间大小为 \(n = \mid \mathcal{X} \mid\) 的离散型随机变量 \(X\)，其经验分布的概率质量函数为 \(\hat{p}(X = x) = \frac 1 n\)，于是有

代入到 PPL 后得到

联合熵 (Joint Entropy)

联合熵是度量一组随机变量的联合分布熵，其定义为

其中 \(\mathcal{X}\) 是样本空间， \(p(x_1, x_2, …, x_m)\) 是 \(X_1, X_2,…, X_m\) 的联合概率分布。

熵率 (Entropy Rate)

熵率是关于随机过程的熵，对于一个随机过程 \(\eta\) 来说，对应一组随机变量序列 \(X_1, X_2,…, X_m\)，设这个序列的联合熵为 \(H_m(X_1, X_2,…, X_m)\)，则 \(\eta\) 的熵率定义为

渐进均分性质（AEP）

若将 \(-\log_2{p_\eta(x_1,x_2,…,x_m)}\) 视作序列 \(x_1,x_2,…x_m\) 的信息量，则熵率 \(H(\eta)\) 可以看作是序列 \(X_1,X_2,…X_m\) 在所有可能取值上的期望信息量，注意这是关于无限长序列所有可能取值的量。根据Shannon-McMillan-Breiman 定理，如果随机过程满足遍历性(ergodic)条件和平稳性(stationary)条件，则对于任意无限长序列 \(X_1, X_2, …, X_m\)，其联合分布概率的负对数除以 \(m\) 收敛到熵率，即

随机过程之间的交叉熵

类似于概率分布间的交叉熵定义，我们可以根据熵率来定义随机过程间的交叉熵，即对于两个随机过程 \(\eta\) 和 \(\xi\)，在随机变量序列 \(X_1, X_2,…, X_m\) 上的交叉熵定义为

同样地，如果 \(\eta\) 满足遍历性和平稳性条件，根据渐进均分性质，上式可以简化为

随机过程的困惑度

随机过程在每个时间点都对应一个概率分布，因此仿照前面使用熵来定义概率分布的困惑度，这里也可以使用熵率来定义随机过程的困惑度，即对于随机过程 \(\eta\)

语言模型

语言模型可以看作是一组概率模型，其中在每个时间点上的概率模型都是对真实世界语言概率分布的建模，具体来说，给定一个 token 序列，语言模型可以给出下一个 token 出现的概率，这里我们用 \(p_\xi(X_i \mid X_{<i})\) 表示。另外，利用条件概率公式，通过语言模型也可以计算整个句子的概率

语言模型的困惑度

语言模型在每个时间点都是对真实世界语言概率分布的建模，因此可以将语言模型看作是真实世界语言随机过程的模型，类似于概率模型的困惑度定义，语言模型的困惑度应该由语言模型本身与真实世界语言随机过程之间的交叉熵来计算，即

若语言模型同时满足平稳性和遍历性条件，则 \(H(\eta, \xi)\) 又可以写为

• 注：关于将渐进均分性质应用到交叉熵的化简我没有找到具体的证明过程，看到的文章基本都是一笔带过，不过结论应该是正确的。

自回归语言模型的困惑度计算

以上内容我们从原理上讨论了语言模型的困惑度，接下来将考虑如何计算一个自回归语言模型的困惑度。所谓自回归语言模型，指的是使用自回归方法训练的语言模型，具体来说，它使用 token 序列前面的 tokens 来预测下一个 token，然后再与真实的 token 进行比较，从而计算交叉熵损失，这是一种典型的非监督学习方法，目前几乎所有的生成式 LLM 都是使用这种方法进行训练的，所以我们这里只讨论这种类型的语言模型。

根据前面推导的交叉熵计算公式

这里需要 \(m\) 趋近于无限，但在实际应用中，显然无法处理无限长的序列，所以我们只能使用有限长的数据近似计算，并且 LLM 还存在 context length 限制，于是还需要将评估数据集分割成多个不长于 context length 的子序列，然后分别计算，最后取平均值。也就是说

其中 \(C\) 为 context lenght，\(N\) 为子序列数量。

对于一个自回归语言模型来说，输入一个 token 序列，例如 \([x_0, x_1,…, x_{i-1}]\)，它预测的下一个 token \(x_i\) 的概率为 \(p_\xi(x_i\mid x_{\lt i})\)，从代码上来说，以 gpt2 为例，这就是模型输出的 logits 经过 softmax 后的结果。

with torch.no_grad():
    outputs = model(input_ids)
    logits = outputs.logits
    logits = logits[:, :-1] ## 预测token的logits
    probs = F.softmax(logits, dim=-1)

对于一个给定的序列，\(x_i\) 是已知的，设它在词表中的 id 为 k，那么语言模型给出的概率 \(p_\xi(x_i\mid x_{\lt i})\) 就是 probs[k]。

使用模型输出的 logits，我们可以计算所有的 \(p_\xi(x_i\mid x_{\lt i}), i = 1,2,…,m\)。下面以 gpt2 在 WikiText2 数据集上的困惑度计算为例，这部分我们参考 huggingface 的 perplexity 页面

from datasets import load_dataset
from transformers import AutoTokenizer, GPT2LMHeadModel
from tqdm import tqdm
import torch
import numpy as np

tokenizer=AutoTokenizer.from_pretrained("gpt2")
model=GPT2LMHeadModel.from_pretrained("gpt2")
device = "cuda"
model.to(device)
model.eval()

test = load_dataset("wikitext", "wikitext-2-raw-v1", split="test")
encoding = tokenizer("\n\n".join(test["text"]), return_tensors="pt")

## 序列总长度
seq_len = encoding.input_ids.shape[1]
## context length
C = 1024

log_prob = []
for begin_loc in tqdm(range(0, seq_len, C)):
  end_loc = min(begin_loc + C, seq_len)
  input_ids = encoding.input_ids[:, begin_loc: end_loc].to(device)
  with torch.no_grad():
    outputs = model(input_ids)
    logits = outputs.logits
    logits = logits[:, :-1]
    labels = input_ids[:, 1:]
    probs = torch.softmax(logits, dim=-1)
    probs = probs.squeeze(0)
    labels = labels.squeeze(0)
    target_probs = torch.gather(probs, 1, labels.unsqueeze(1))
    log_prob.extend(target_probs.log2().cpu().numpy().tolist())
  
  if end_loc == seq_len:
    break  

ce = - np.sum(log_prob) / len(log_prob)
ppl = 2 ** ce

最终结果为 29.94，这和 gpt2 论文中报告的结果 29.41 相近。需要注意的是，huggingface 中使用了模型输出的交叉熵损失，我们这里显式的写出了计算过程，两者是等价的。

总结

本文从基础概念出发，逐步推导了概率分布的困惑度，随机过程的困惑度，以及语言模型的困惑度，最后给出了自回归语言模型困惑度的计算方法。

参考

• https://www.seas.ucla.edu/spapl/weichu/htkbook/node218_mn.html

• https://www.statlect.com/asymptotic-theory/empirical-distribution

• https://www.mdpi.com/1099-4300/20/11/839