分析 GPT 模型自回归生成过程中的 KV Cache 优化技术

类 GPT 模型在自回归生成过程中，每一次推理只生成一个 token，然后将生成的 token 拼接到输入序列，再进行下一次推理，直到生成 eos 或者达到最大长度。在这个过程中，每次推理的计算量都会增加，假设每个 token 的计算量为 1 个单位，则在 context 的长度为 $L$，生成序列长度为 $M$ 的情况下，总的计算量为 $(M + 1) L + \frac{M (M + 1)} 2$ 个单位。

KV Cache 的使用者认为上述过程的大部分运算是可以避免的，比如每个 token 输入模型之后，内部的 key 和 value 可以缓存起来，后续就不必再计算了。也就是说除了第一次推理是将 整个prompt 输入模型，后续每次推理都是将新生成的 token 作为输入，这样总的计算量就减小到了 $L + M$ 个单位。

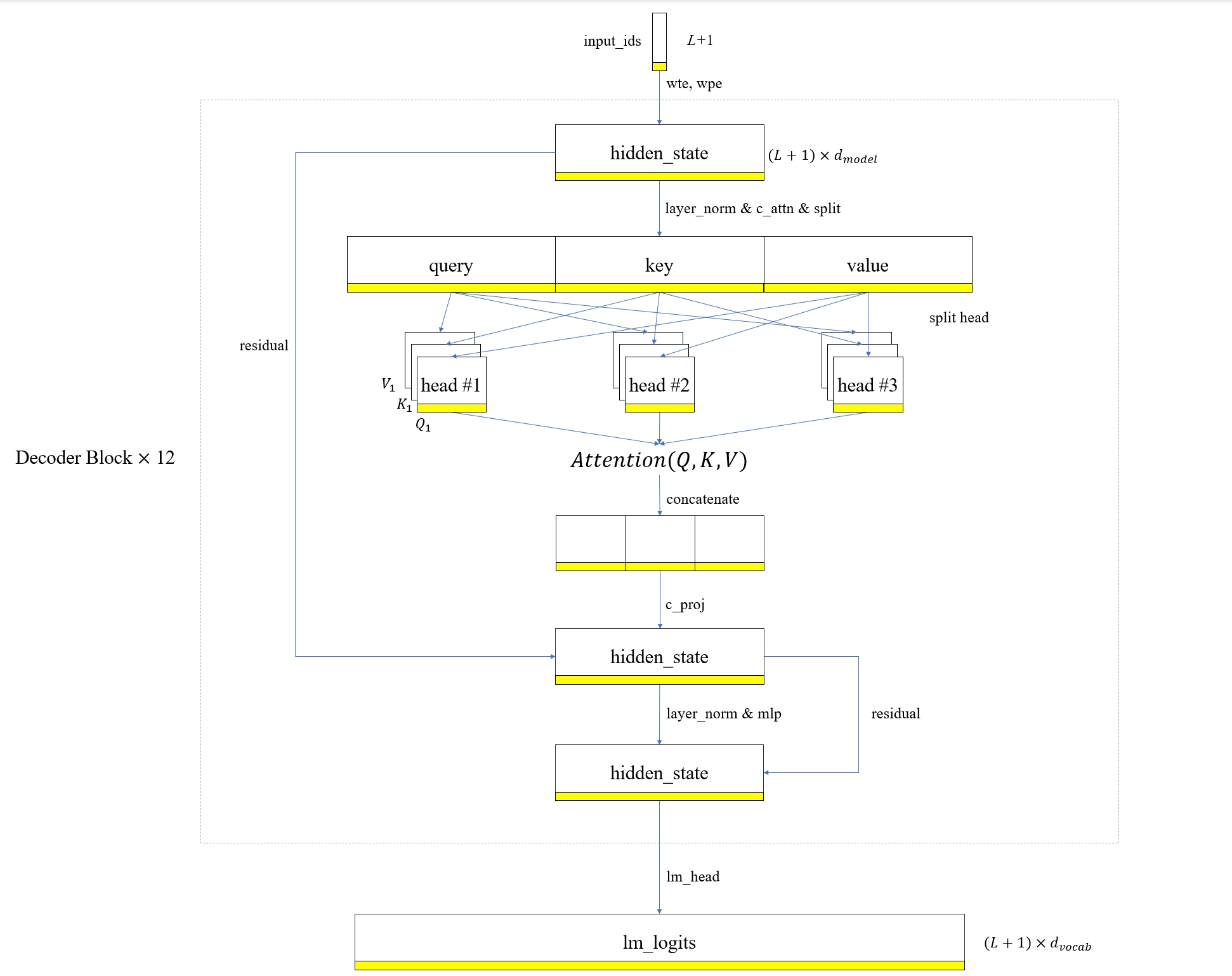
本文将以 GPT2 模型结构为例，从计算的角度分别分析这两种方法，并说明为何它们是等价的。首先观察常规输入的模型推理流程

1. 这里，我们的输入是一个长度为 $L$ 的序列，加上前次推理生成的 token（图中的黄色部分），wte 和 wqe 是 GPT2 的 embedding 权重矩阵，它们将 input_ids 和 position_ids 映射到高维空间，得到 hidden_state 张量。

2. c_attn 是 GPT2 的线性变换模块，它将 hidden_state 的维度提升 3 倍，然后分割成 query，key 和 value。

3. 将 query，key 和 value 分割成多个 head 之后，分别进行注意力计算，再将多个 head 的结果拼接起来。最后使用 c_proj 进行线性变换。

4. 将新计算的 hidden_state 与之前的 hidden_state 相加，也就是残差连接。再通过 mlp 模块，最后再次残差连接。

5. 通过 lm_head 模块生成 logits，即预测 token 的概率分布。

图中张量里面的黄色条带一开始表示的是输入序列的最后一个 token，随着前向计算的进行，它逐渐变成了下一个 token 的概率分布，也就是 logits 的最后一行，而 logits 前面的行在推理阶段都是没有意义的。既然如此，那我们不禁思考，是否可以只计算最后一行，从而省略其他行的计算量？要回答这个问题，需要回溯推理过程中的每个步骤，并观察最后一行是否对前面的行有依赖，如果没有依赖，那自然是可以省略的。

1. 首先我们分析 lm_head 模块，它其实就是一个线性映射，将 hidden_state 的维度从 d_model 变换到 vocab_size，根据矩阵乘法的性质，可以知道 logits 的最后一行只与 hidden_state 的最后一行相关。

2. 同样的道理，mlp 模块是多个线性变换和激活函数的组合，因此它的输出也只与输入 hidden_state 的最后一行相关。

3. 对于 layer_norm 来说，它是在 d_model 方向上计算均值和方差，然后进行归一化，因此它的输出也只与输入 hidden_state 的最后一行相关。

4. c_proj 也是一个线性变换，因此它的输出也只与输入 hidden_state 的最后一行相关。

5. 最前面的 wte，wqe 以及 c_attn 都是线性变换，因此它们的输出也只与输入 hidden_state 的最后一行相关。

接下来我们重点分析一下 Attention 模块，它的计算过程如下

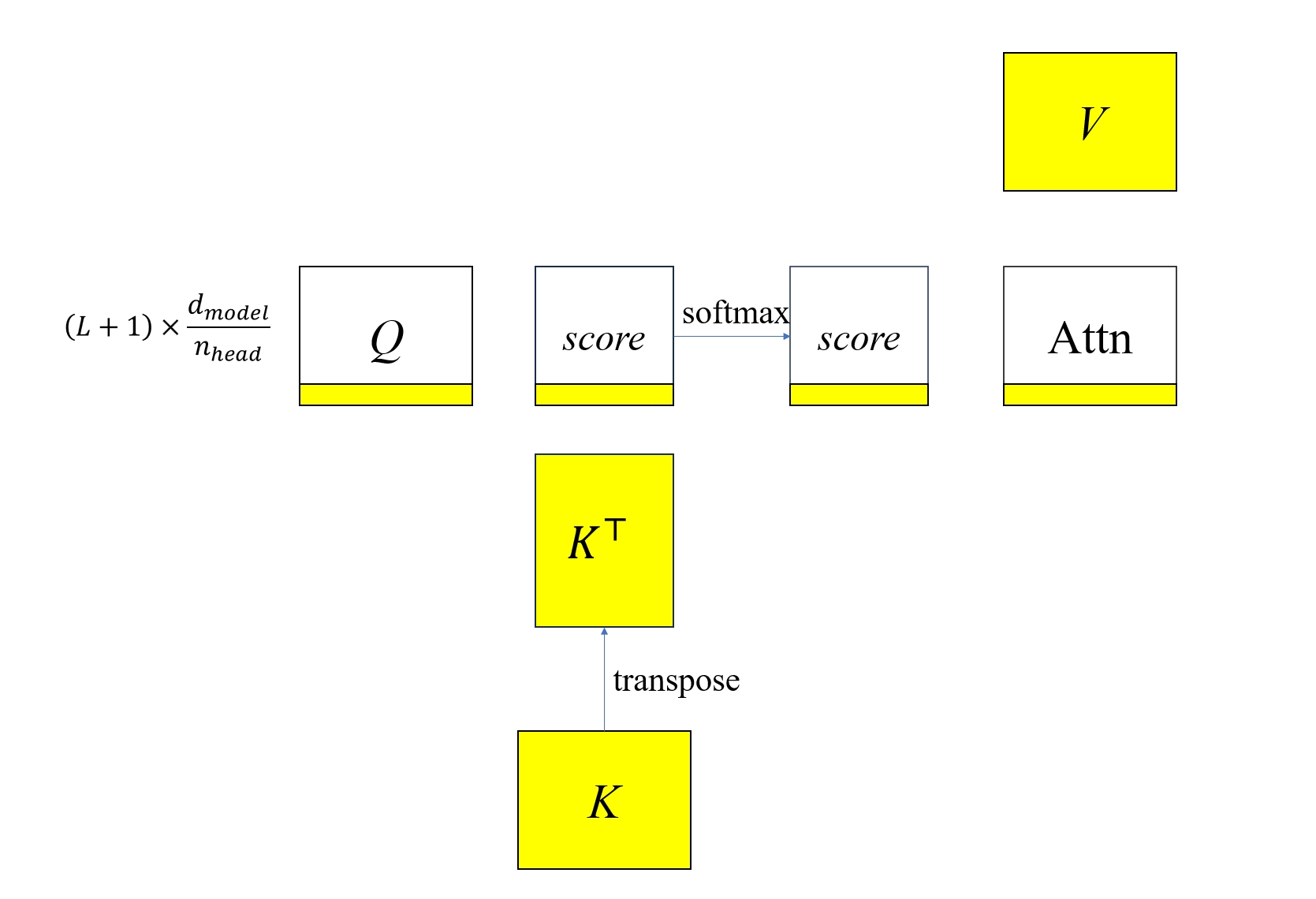
图中 Attn 的最后一行仅与 score 的最后一行相关，但和全部的 V 相关，而 score 则与 Q 的最后一行相关，与 K 的全部相关。因此可以得到，Attn 的最后一行与 Q 的最后一行，以及完整的 K 和 V 相关。这个结论相当重要，因为它揭示了为什么我们要使用 KV Cache 而不是 QKV Cache。

下面我们再把 Attention 计算中的不相关部分去掉，如下图所示

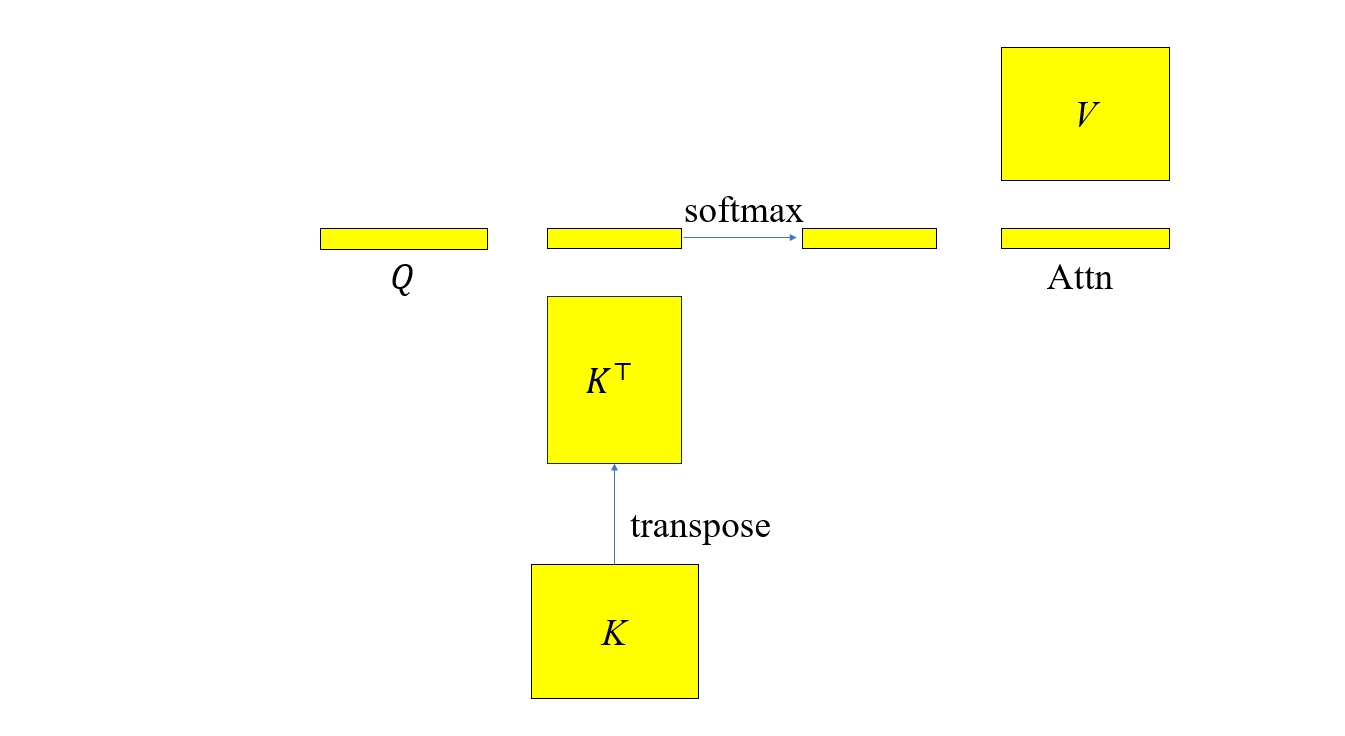
然后再把整个模型计算过程中的不相关量去掉，得到下图

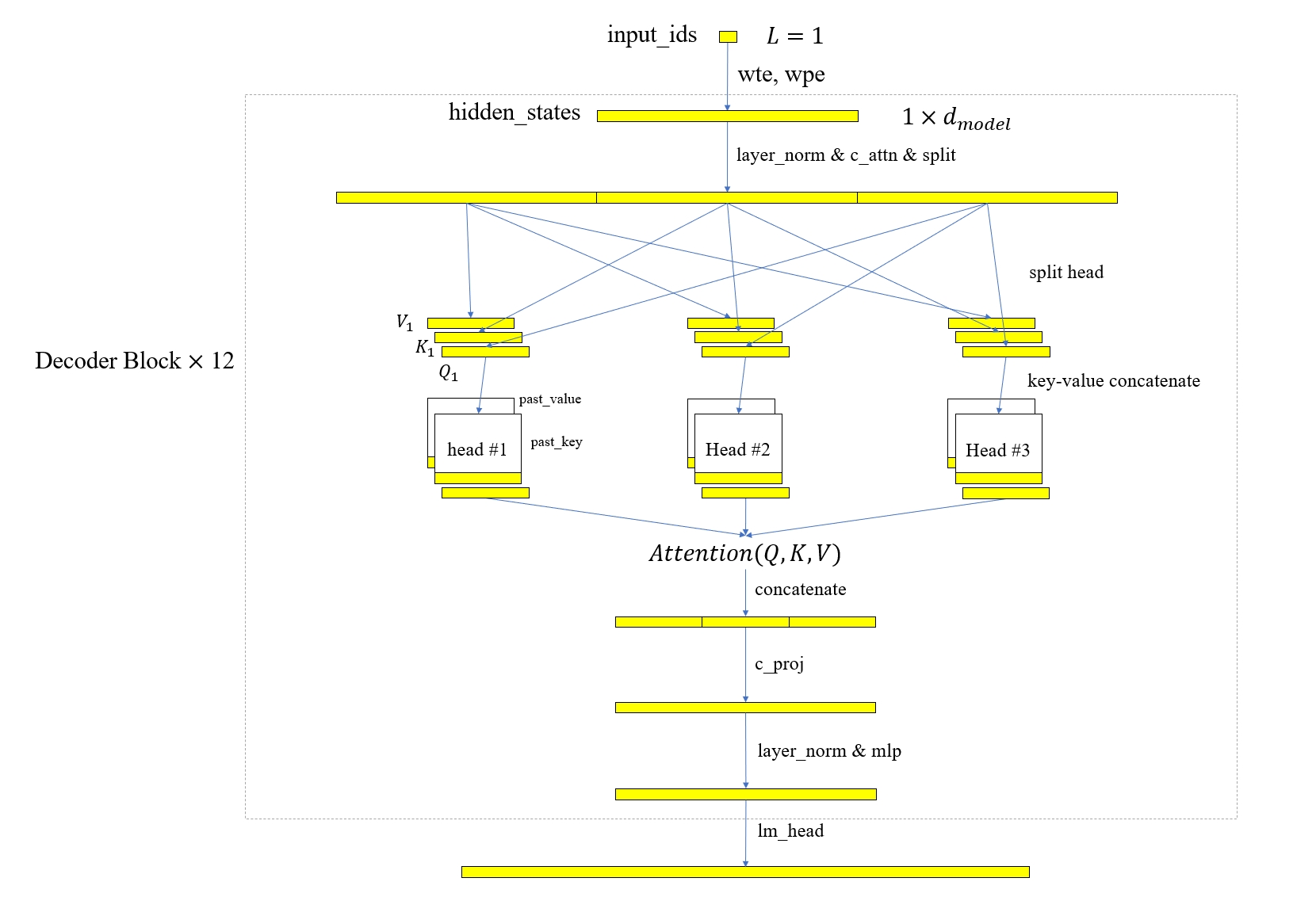
可以看到这时模型的输入只有上一次推理生成的 token，而不是整个 prompt 序列，且在进行注意力计算之前需要拼接完整的 key 和 value，所以需要将这两个量缓存起来，并在每次推理时复用。

通过以上的分析，证明了使用 KV Cache 和正常的输入全序列计算是等价的，但是计算量大大减少了，因此 KV Cache 成了现在类 GPT 模型生成过程中的的标配技术。