图解自动微分的正向模式和逆向模式
自动微分建立在复合函数求导的链式规则之上,考虑以下复合函数
\[f(x) = a(b(c(x)))\]则 \(f\) 对 \(x\) 的导数为
\[\frac{\mathrm{d}f}{\mathrm{d}x} = \frac{\mathrm{d}f}{\mathrm{d}a} \frac{\mathrm{d}a}{\mathrm{d}b} \frac{\mathrm{d}b}{\mathrm{d}c} \frac{\mathrm{d}c}{\mathrm{d}x}\]显然,上述公式存在两种计算顺序,第一种先对高阶函数求导,我们称之为逆向模式
\[\frac{\mathrm{d}f}{\mathrm{d}x} =\left( \left(\frac{\mathrm{d}f}{\mathrm{d}a} \frac{\mathrm{d}a}{\mathrm{d}b} \right) \frac{\mathrm{d}b}{\mathrm{d}c} \right) \frac{\mathrm{d}c}{\mathrm{d}x}\]第二种先对低阶函数求导,我们称之为正向模式
\[\frac{\mathrm{d}f}{\mathrm{d}x} = \frac{\mathrm{d}f}{\mathrm{d}a} \left( \frac{\mathrm{d}a}{\mathrm{d}b} \left( \frac{\mathrm{d}b}{\mathrm{d}c} \frac{\mathrm{d}c}{\mathrm{d}x} \right) \right)\]为了更直观地说明两种模式的区别,我们考虑一个简单的例子
\[f(x, y, z) = \log(xy) + \sin(z)\]它的计算图如下所示

我们最终需要计算偏导数 \(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\)。下面我们首先推导正向模式自动微分:
- 计算 \(v_1 = xy\),得到 \(\frac{\partial v_1}{\partial x}, \frac{\partial v_1}{\partial y}\)
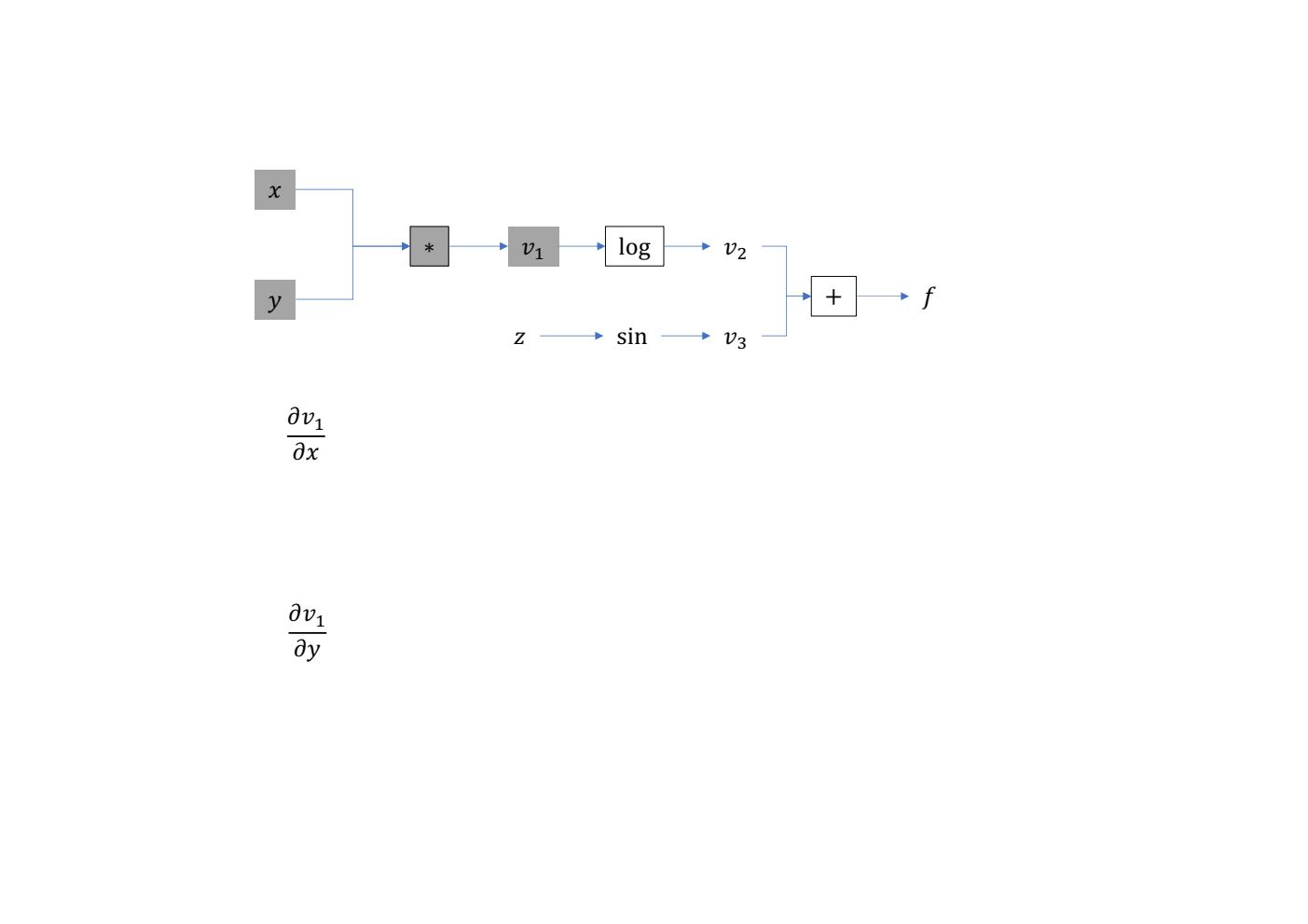
- 计算 \(v_2 = \log(v_1)\),得到 \(\frac{\partial v_2}{\partial v_1}, \frac{\partial v_2}{\partial x}, \frac{\partial v_2}{\partial y}\)
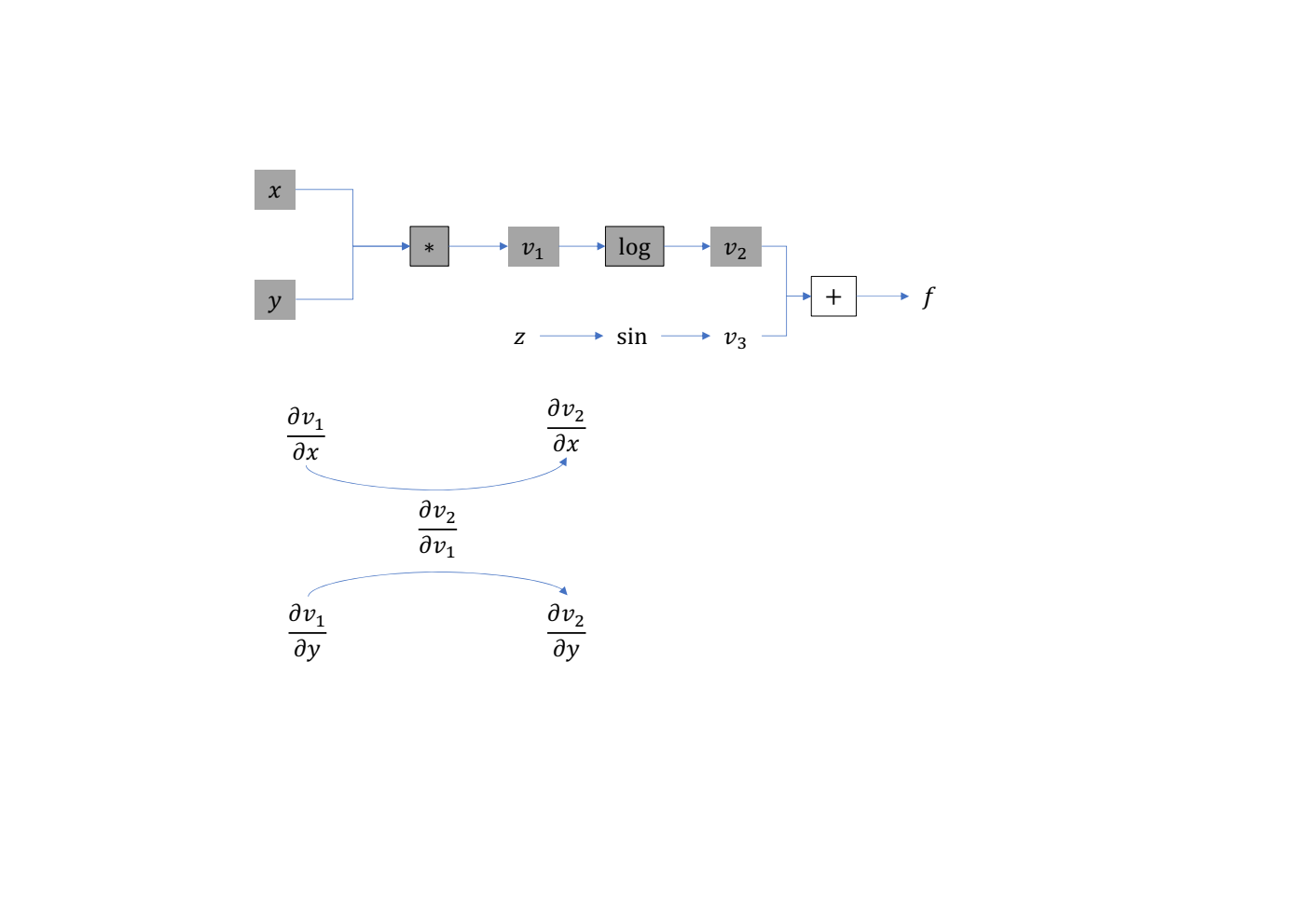
- 计算 \(v_3 = \sin(z)\),得到 \(\frac{\partial v_3}{\partial z}\)
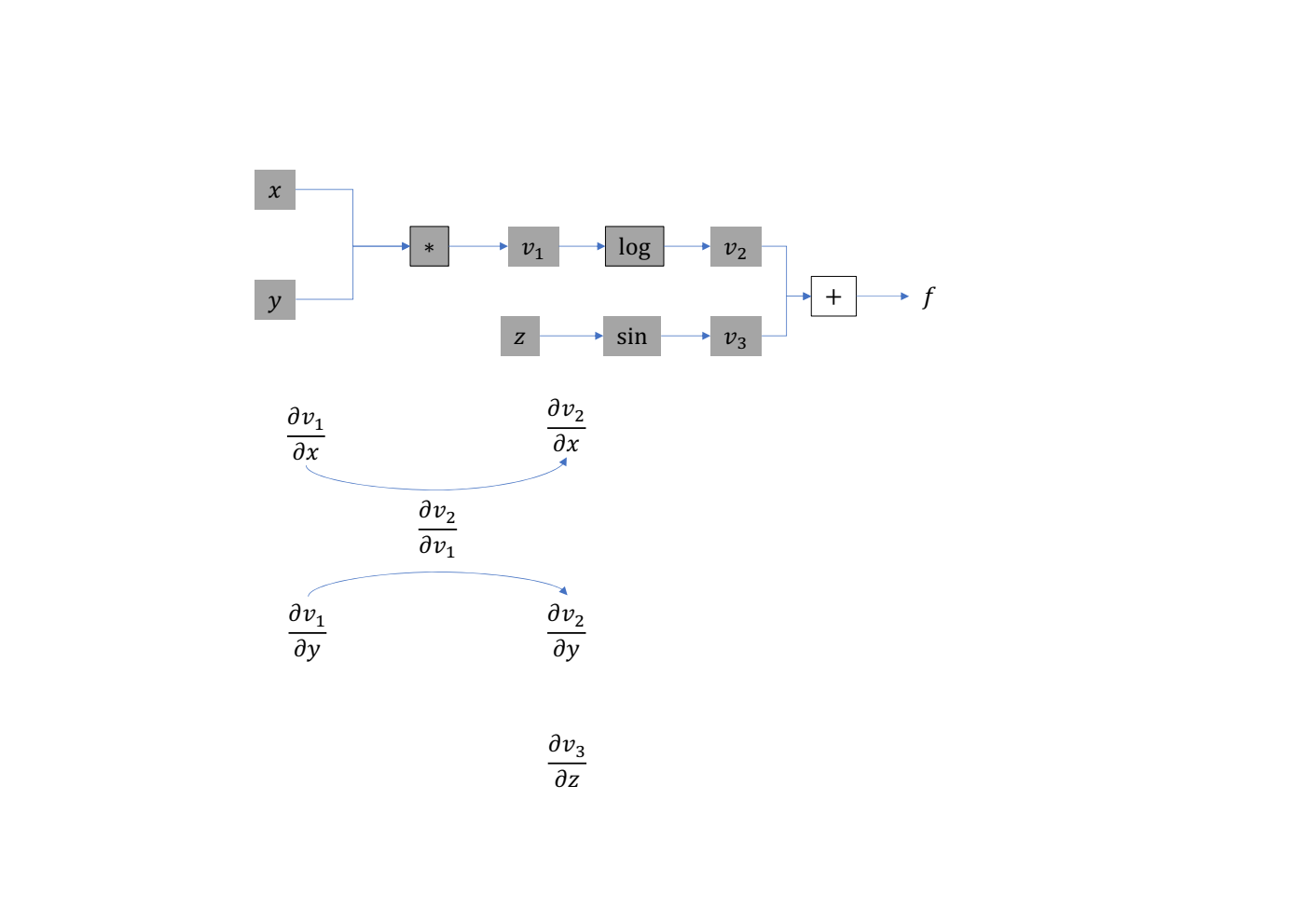
- 计算 \(f = v_2 + v_3\),得到 \(\frac{\partial f}{\partial v_2}, \frac{\partial f}{\partial v_3}, \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z}\)
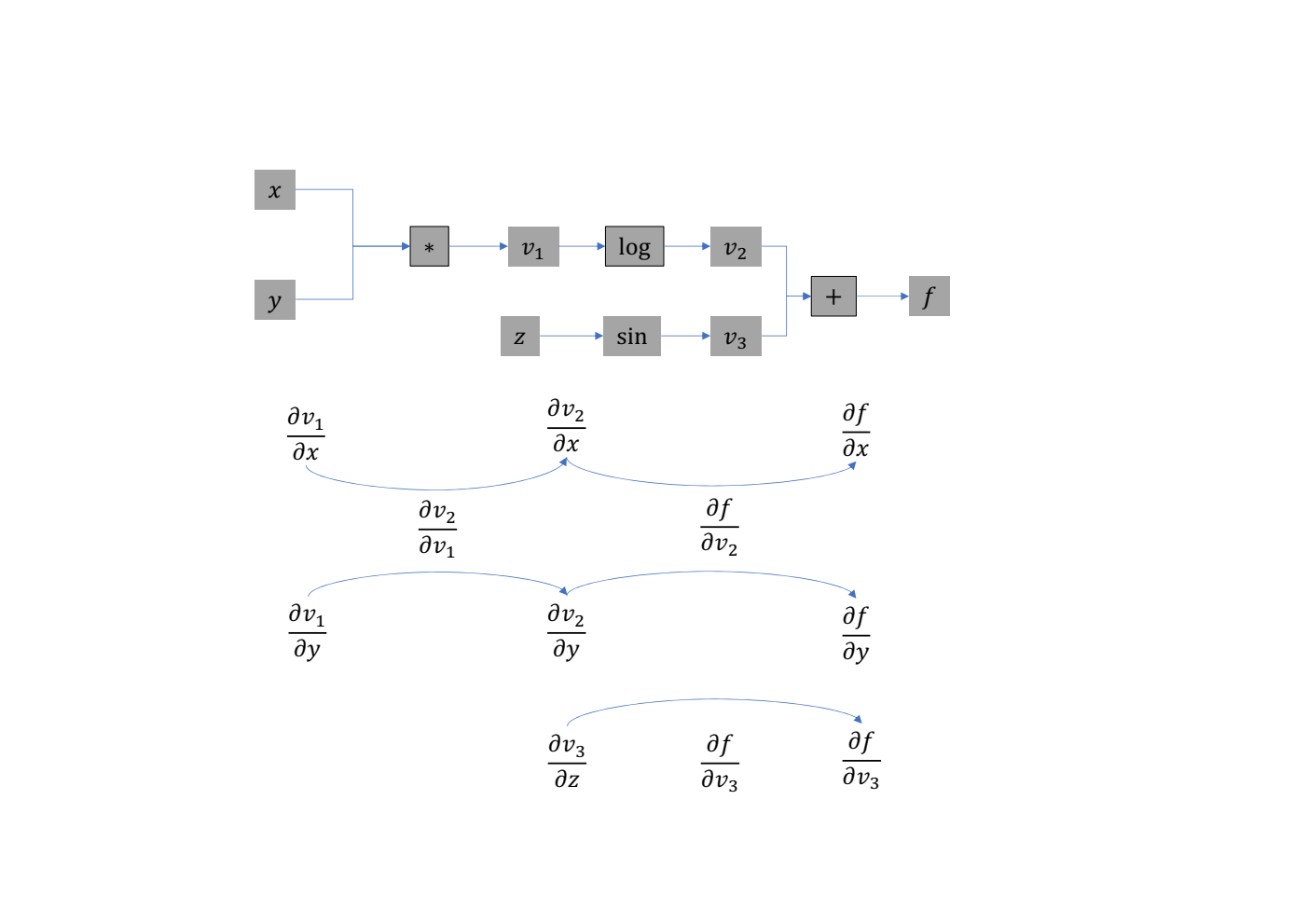
可以看到,随着计算图的向前推进,我们也不断地得到最新值对输入的梯度,所以这种计算方式也称为自动微分的正向模式。
接下来我们再描述另一种计算模式:
- 计算 \(v_1 = x y\),并构造另一张计算图,形状与原计算图类似,但描述的是梯度计算关系,这里插入乘法的梯度计算节点
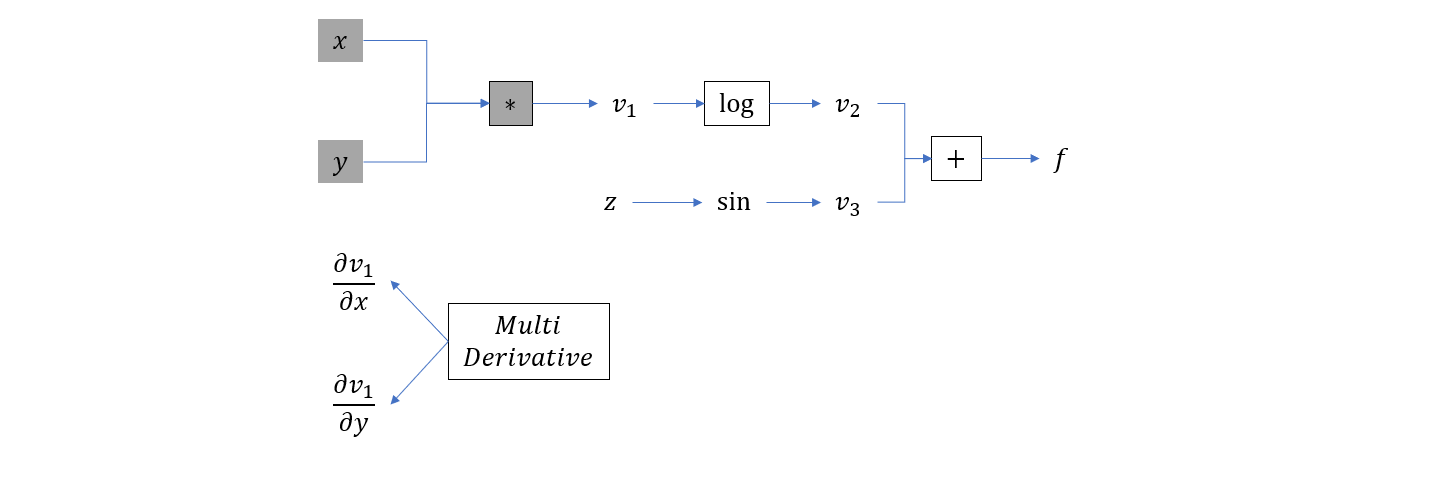
- 计算 \(v_2 = \log(v_1)\),插入
log运算的梯度计算节点
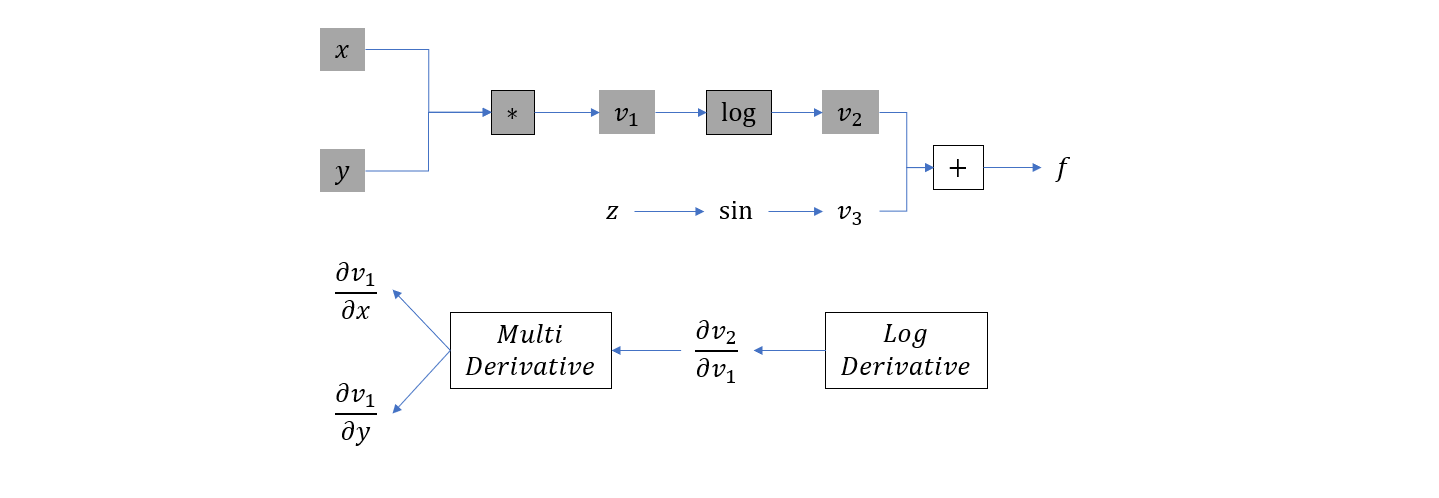
- 计算 \(v_3 = \sin(z)\),插入
sin运算的梯度计算节点
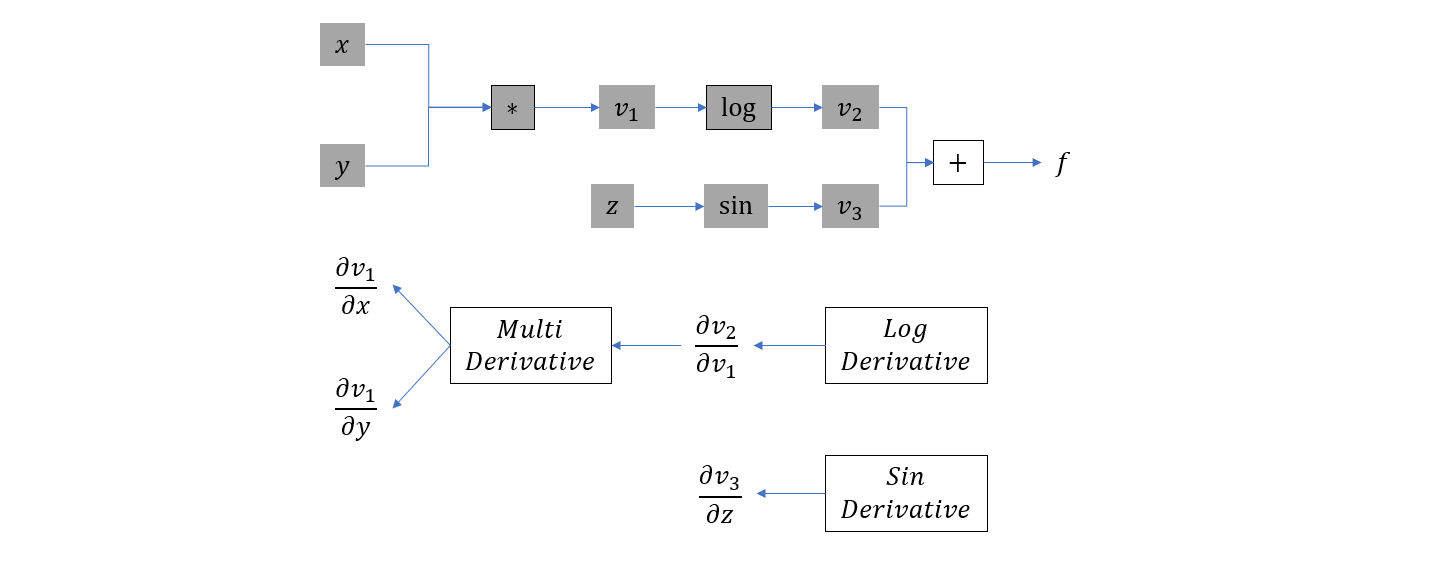
- 计算 \(f = v_2 + v_3\),插入加法的梯度计算节点
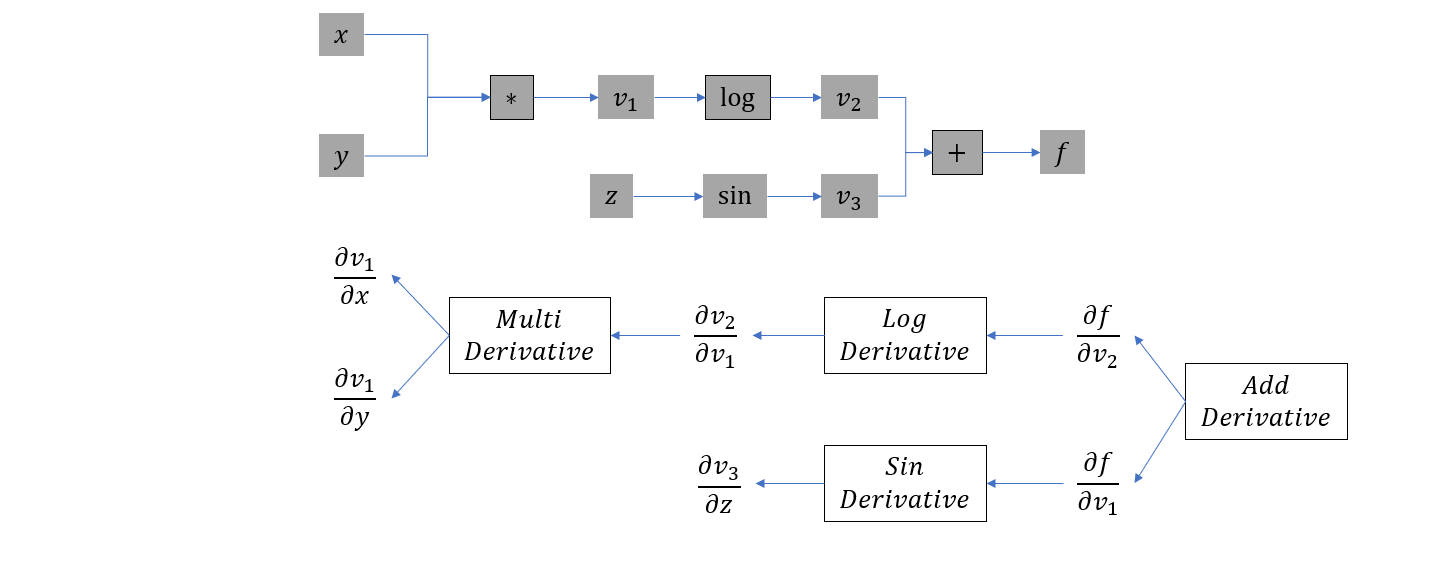
最后再以原计算图相反的方向遍历梯度计算图,从而得到 \(f\) 对 \(x, y, z\) 的梯度。这就是自动微分的逆向模式。