如何自底向上地建立起对 Monad 的理解

原群 (Magma)

如果存在一个集合 \(M\) 以及建立在其元素间的二元运算 \(\star\)，满足 \(\forall x, y \in M\)，有 \(x \star y \in M\)，则称这样的集合为原群，写作 \((M, \star)\)。

半群 (Semigroup)

如果一个原群 \(M\) 的二元运算满足结合律性质，即 \(\forall x, y, z \in M \)，都有 \(x \star y \star z = x \star (y \star z)\)，则称这样的结构为半群。

幺半群 (Monoid)

在半群的基础上，如果其中的二元运算存在单位元，即，\(\exists e \in G\)，\(\forall x \in G\)，使得 \(x\star e = e \star x= x\)，则称这样的结构为幺半群。

群（Group）

在半群的基础上，如果还满足逆元素性质，即 \(\forall x \in G, \quad\exists x^{-1} \in G\) ，使得 \(x\star x^{-1} = e\)，则称这样的结构为群。

群同构

假设有两个群 \((G_1, \times)\) 和 \((G_2, \star)\)，以及双射映射 \(\phi: G_1 \rightarrow G_2\) ，满足以下条件

\(\forall x, y \in G_1\)，都有 \(\phi(x\times y) = \phi(x)\star \phi(y)\)

那么，群 \((G_1, \times)\) 和 \((G_2, \star)\) 同构。

态射 (Morphism)

态射是一种对数学对象之间关系的高层次抽象，比如集合中的函数关系 \(f: S_1 \rightarrow S_2 \)，群的同构关系 \(\phi: G_1 \rightarrow G_2\) 等等，它们的共同点是都从一个对象指向了另一个对象，我们用术语箭头来命名这种关系，因此我们可以称态射是两个对象之间的箭头。

同函数类似，态射之间也可以组合，比如 \(\phi: G_1 \rightarrow G_2\) 和 \(\psi: G_2 \rightarrow G_3\) 之间的组合为 \(\psi \circ \phi : G_1\rightarrow G_3\)，其中，组合符号 \(\circ\) 也可以看作是以态射为对象的二元运算

类(Class)

类是一组数学对象的统称，这些对象是类的元素，虽然这听起来有点像集合的概念，但类正是为了修正集合论的缺陷而提出来的。举个例子，“所有的集合放在一起构成集合”这种论断会导致悖论，因此在ZFC公理系统之后，集合的范围被限制了。于是“所有的集合”不构成一个集合，但是“所有的集合”这个概念是存在的，既然不能叫集合，那么就叫类吧。所以类是比集合范围更大的数学概念，集合也被称为小类(small class)，不是集合的类被称为真类(proper class)。

范畴(Category)

范畴（用符号 \(\mathbb{C}\)表示）是这样一种数学结构，它包含一个对象类\(ob(\mathbb{C})\)，以及一个态射类\(hom(\mathbb{C})\)。具有以下性质：

每个态射都对应一个定义域对象和一个对应域对象，可以使用符号 \(f:X \rightarrow Y\) 表示，这里的 \(X, Y \in ob(\mathbb{C})\)。
每一个对象都有一个恒等态射，它的定义域和对应域都是自身，即 \(I_X:X \rightarrow X\)。
对于任意一对态射 \(g, f\)，如果 \(f\) 的对应域等于 \(g\) 的定义域，即 \(f: X\rightarrow Y, g: Y\rightarrow Z\)，那么它们可以构成组合态射 \(g\circ f: X\rightarrow Z\)。

并且有以下公理：

\(\forall f: X \rightarrow Y \in hom(\mathbb{C})\)，有 \(I_Y \circ f = f\circ I_X = f\)。
对于任意三个可组合的态射，例如 \(f: X\rightarrow Y, g: Y\rightarrow Z, h: Z\rightarrow W\)，有 \((h \circ g) \circ f = h \circ (g\circ f)\)，也就是说，态射组合满足结合律。

如果\(ob(\mathbb{C})\) 和 \(hom(\mathbb{C})\) 都是集合，那么 \(\mathbb{C}\) 又被称为小范畴。

值得一提的是，幺半群等价于只有一个对象的范畴。为了说明这一点，我们假设只有一个对象 \(p\) 的小范畴 \(\mathbb{M}\)，根据定义，\(\mathbb{M}\) 的态射类是从 \(p\) 到 \(p\) 的态射集合，即 \(hom(\mathbb{M}) = {f\mid f: p\rightarrow p}\)，那么 \(\forall f, g \in hom(\mathbb{M})\)，都有\(g\circ f \in \mathbb{M}\)，也就是说，这里的态射组合满足封闭性质，另一方面，设 \(p\) 的恒等态射为 \(I_p\)，那么根据前面的公理可知 \(\forall f \in hom(\mathbb{M})\)，有 \(I_p \circ f = f \circ I_p = f\)，也就是说，范畴 \(\mathbb{M}\) 中的态射组合存在单位元。根据以上两点，再考虑到态射组合满足结合律，我们可以说，在单对象范畴中，以态射为元素，态射组合为二元运算，构成一个幺半群，它们的概念对应关系如下：

幺半群	单对象范畴
元素	态射
二元运算	态射复合
单位元	恒等态射

举个简单的例子，所有整数构成的集合 \(\mathcal{N}\) 在加法运算上是一个幺半群，它的元素是整数值，比如 1，2，3等等，二元运算就是加法，单位元就是 0。从范畴的角度来看，整个集合 \(\mathcal{N}\) 就是一个对象，态射类是从 \(\mathcal{N}\) 指向 \(\mathcal{N}\) 的态射集合。对于集合来讲，一个态射 \(f: \mathcal{N}\rightarrow \mathcal{N}\) 可以是一个函数，它将 \(\mathcal{N}\) 中的元素映射为另一些元素，比如下图所示

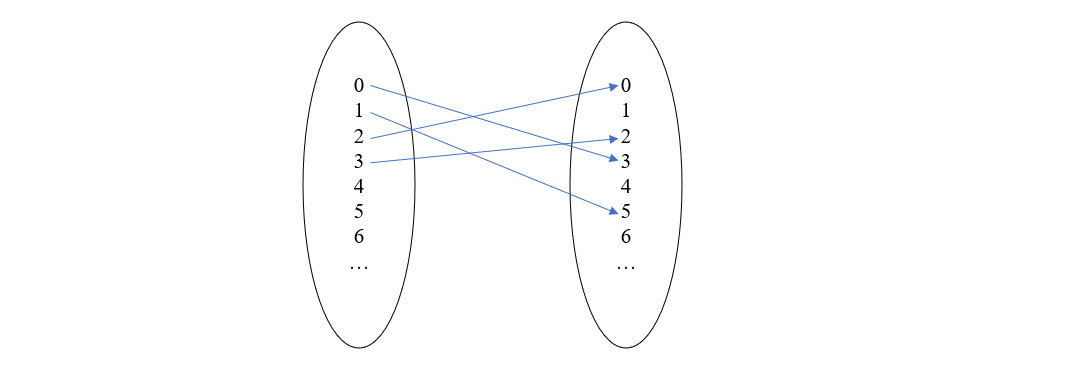
再根据幺半群与单对象范畴的关系，每个整数都对应一个态射，那么我们可以将整数本身看作是函数，这些函数具体是怎么映射的，暂时还不清楚，但我们可以构造出来。首先，它们之间的组合必须和幺半群中的加法运算相容，比如在幺半群的概念中 \(1+2 = 3\)，那么在范畴的概念中就必须有 \(1\circ 2 = 3\)。为了符合这一条件，我们定义函数 \(n(x) = x + n\)，举例来说，函数 1 的映射图如下

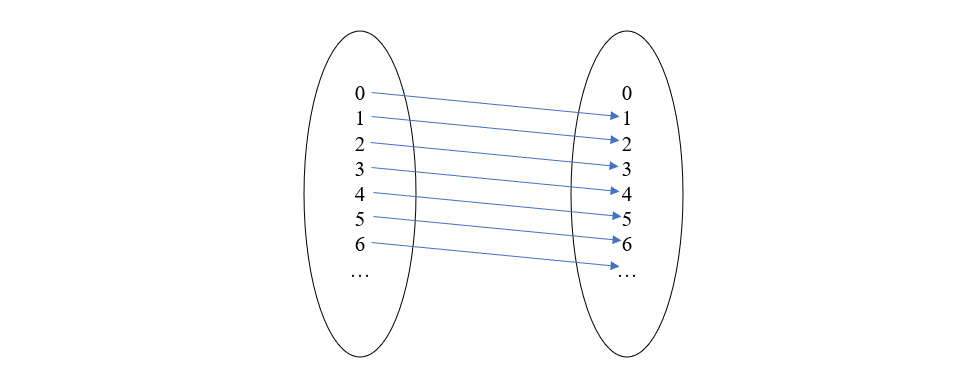
使用这种定义，函数 1 和 2 的组合效果等于函数 3 （即 \(2(1(x)) = 3(x)\)），并且函数 0 可以作为函数组合的单位元（即 \(n(0(x)) = n(x)\)）。总结起来就是，以整数集 \(\mathcal{N}\) 作为对象，以每个整数作为态射，并按上述方式构造映射，那么此对象和态射类构成一个范畴。

终结对象(Terminal Object)

终结对象都是范畴中的特殊对象，特殊之处在于它的态射相关性质。设有范畴 \(\mathbb{C}\)，若 I 为终结对象，那么 \(\forall X \in \mathbb{C}\)，只存在唯一态射 \(!: X \rightarrow I\)。

集合范畴 (Set)

集合范畴是由集合作为对象构成的范畴，它的态射是集合间的映射，也就是函数，而恒等态射就是集合对象到自身的函数。集合范畴的终结对象是任意单元素集合，这一论断是显然的，由于只有一个元素，所以任意集合到单元素集合的函数只有一种映射方式，也就是把所有元素映射到这个单元素上。

从范畴的观点来看，其对象不能用集合的语言来表述，也就是说，我们不能讲某个元素属于对象，因为这种论断在范畴的概念下没有意义，但是我们可以在范畴中找到一种结构来表示与元素相同的概念。设范畴 \(\mathbb{C}\)，以及其中的一个终结对象 \(I\)，再设另外两个对象 \(X, Y \in ob(\mathbb{C})\)，以及态射 \(\mu:X \rightarrow Y, a: I \rightarrow X\)。根据态射的复合性，可以证明 \(\mu \circ a: I \rightarrow Y\)，若令 \(b = \mu \circ a\)，那么就有 \(b: I \rightarrow Y\)。

把以上表述换成集合的语言其实就是：对于元素 \(a\in X\)，如果有函数 \(\mu: X\rightarrow Y\)，则 \(b=\mu(a) \in Y\)。可以看到，终结对象到对象的态射具有和集合元素相同的结构。这一结论相当重要，是后面我们理解范畴中的幺半群的关键。

积范畴 (Product Category)

类似于集合的笛卡尔积的概念，范畴 \(\mathbb{C}, \mathbb{D}\)的积范畴的构造过程如下：

对象： \(\forall x \in ob(\mathbb{C}), y \in ob(\mathbb{D})\)，有序对 \((x, y) \in ob(\mathbb{C}\times \mathbb{D})\)
态射： \(\forall f \in hom(\mathbb{C}), g \in hom(\mathbb{D})\)，有序对 \((f, g) \in hom(\mathbb{C}\times \mathbb{D})\)
态射组合：\(\forall f_1, f_2 \in hom(\mathbb{C}), g_1, g_2 \in hom(\mathbb{D})\)，\((f_1, g_1) \circ (f_2, g_2) = (f_1 \circ g_1, f_2 \circ g_2)\)
恒等态射： \(\forall x \in ob(\mathbb{C}), y \in ob(\mathbb{D})\)，有 \(I_{(x, y)} = (I_x, I_y))\)

函子 (Functor)

以范畴作为对象，范畴与范畴之间的态射又被称为函子，函子将一个范畴的对象和态射映射到另一个范畴的对象和态射。设函子 \(F: \mathbb{C} \rightarrow \mathbb{D}\)，则

\(\forall x \in ob(\mathbb{C}) \Rightarrow F(x) \in ob(\mathbb{D})\)
\(\forall f: x \rightarrow y , \exists g \in hom(\mathbb{D})\)，使得 \(F(f) =g: F(x) \rightarrow F(y) \)
函子 \(F\) 将 \(\mathbb{C}\) 中的单位态射映射成了 \(\mathbb{D}\) 中的单位态射： \(F(id_C) = id_{D}\)
\(\forall f, g \in hom(\mathbb{C}), F(f\circ g) = F(f)\circ F(g)\)

如果一个函子将某个范畴映射到自身，即 \(F: \mathbb{C}\rightarrow \mathbb{C}\)，则该函子又被称为自函子。

自然变换 (Natural transormation) 和自然同构 (Natural isomorphism)

设有范畴 \(\mathbb{C}\) 和 \(\mathbb{D}\)，以及它们之间的两个函子 \(F: \mathbb{C} \rightarrow \mathbb{D}\) 和 \(G: \mathbb{C} \rightarrow \mathbb{D}\)。再设 \(a, b \in ob(\mathbb{C})\)， \(f\) 是 \(\mathbb{C}\) 中的态射，将 \(a\) 态射到 \(b\)，那么 \(Ff\) 将 \(Fa\) 映射到 \(Fb\)，\(Gf\) 将 \(Ga\) 映射到 \(Gb\)。图示关系如下

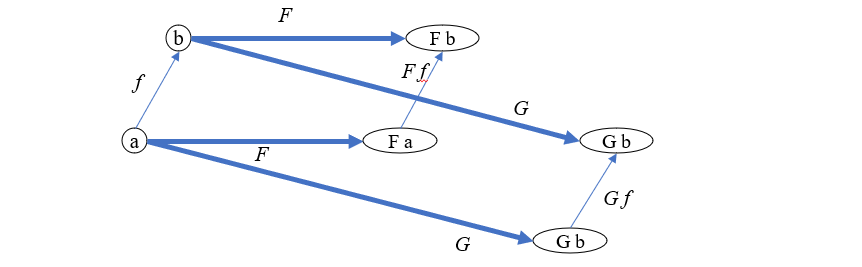
假如存在 \(\mathbb{D}\) 中的态射 \(\eta_a, \eta_b\) 分别将 \(Fa, Fb\) 映射到 \(Ga, Gb\)

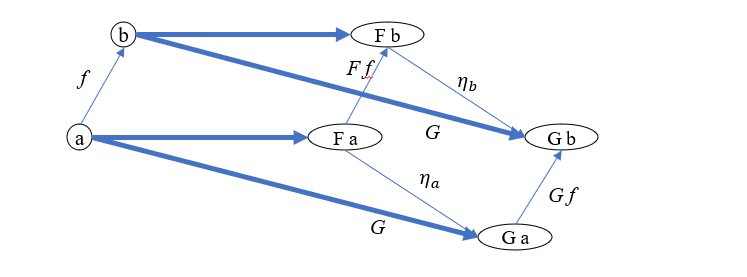
则可以得到

\[Gf \circ \eta_a(Fa) = \eta_b \circ Ff(Fa) = Gb\]

简化写作

\[Gf \circ \eta_a = \eta_b \circ Ff\]

如果对于 \(\forall f \in hom(\mathbb{C})\)，上式都成立，那么 \(\eta\) 就是从 \(F\) 到 \(G\) 的自然变换，\(\eta_a, \eta_b\) 是它的分量。由于 \(\eta\) 将 \(F\) 态射得到的对象 \(F a, F b\) 变换为 \(G\) 态射得到的对象 \(G a, G b\)，所以自然变换又可以看作是函子之间的态射，写作 \(\eta: F \rightarrow G\)。

另外，\(\forall x \in ob(\mathbb{C})\)，如果 \(\eta_x\) 是 \(F x \) 和 \(G x\) 之间的同构，那么 \(\eta\) 又被称为自然同构。

幺半范畴 (Monoidal Category)

考虑范畴 \(\mathbb{C}\)，以及建立在其之上的积范畴 \(\mathbb{C}\times \mathbb{C}\)（也可以用 \(\mathbb{C}^2\)表示），定义它们之间的函子 \(\otimes: \mathbb{C}^2 \rightarrow \mathbb{C}\)，以及某个对象 \(I\in \mathbb{C}\)。

然后，在此基础上再定义两个函子 \(F, G: \mathbb{C}^3 \rightarrow \mathbb{C}\) 分别为

\(F(x, y, z) = (x\otimes y)\otimes z\)
\(G(x, y, z) = x\otimes (y\otimes z)\)。

显然，如果可以的话，我们假设 \(F, G\) 之间存在自然变换 \(a\)，它的分量 \(a_{x, y, z}\) 将 \((x\otimes y)\otimes z\) 态射到 \(x\otimes (y\otimes z)\)，这一过程的图像表示如下

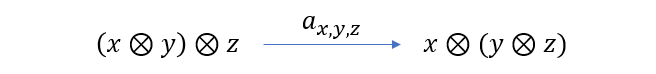
若再进一步假设 \(a\)为自然同构，那么就有 \((x\otimes y)\otimes z\) 同构于 \(x \otimes (y\otimes z)\)。

另外，我们还可以定义三个函子 \(P: {I}\times \mathbb{C} \rightarrow \mathbb{C}, Q: \mathbb{C} \times {I} \rightarrow \mathbb{C}, R: \mathbb{C} \rightarrow \mathbb{C}\)，形式分别为

\(P(I, x) = I \otimes x\)
\(Q(x, I) = x \otimes I\)
\(R(x) = x\)

（其中 \(R\) 可以被称为恒等函子。 \({I}\) 是只包含对象 \(I\) 的单对象范畴）。同样地，我们可以假设 \(P, R\) 之间存在自然变换 \(\lambda\)，分量为 \(\lambda_x : I\otimes x \rightarrow x\)，\(Q, R\) 之间存在自然变换 \(\rho\)，分量为 \(\rho_x : x \otimes I \rightarrow x\)，图像表示如下

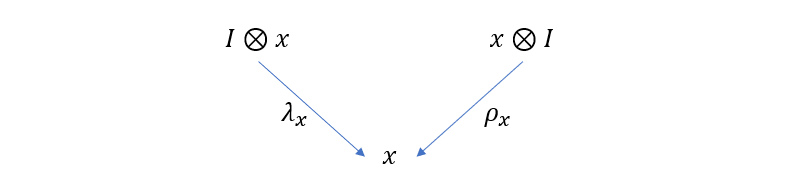
若 \(\lambda, \rho\) 都是自然同构，那么就有 \(I\otimes x \cong x, x \otimes I \cong x\)。

如果以上假设成立，那么我们可以总结出范畴 \(\mathbb{C}\) 的性质：

存在函子 \(\otimes: \mathbb{C}^2 \rightarrow \mathbb{C}\)
存在单元对象 \(I\in \mathbb{C}\)
有一个自然同构 \(a\)，使得 \(\forall x, y, z \in ob(\mathbb{C})\)，有 \((x\otimes y)\otimes z \cong x \otimes (y \otimes z)\)
有一个自然同构 \(\lambda\)，使得 \(\forall x\in ob(\mathbb{C})\)，有 \(I \otimes x \cong x\)
有一个自然同构 \(\rho\)，使得 \(\forall x\in ob(\mathbb{C})\)，有 \(x\otimes I \cong x\)

满足这些性质的范畴就被称为幺半范畴。

举个例子，集合范畴 Set 是由集合构成的范畴，如果我们以集合的笛卡尔积作为 \(\otimes\)，任意单元素集合作为 \(I\)，那么可以得到如下结论：

对于任意三个集合 \(A, B, C\)，集合 \({((x, y), z)\mid x\in A, y\in B, z\in C}\) 与集合 \({(x, (y, z))\mid x\in A, y\in B, z\in C}\) 同构
对于任意集合 A 与单元素集合\({e}\)，集合 \({(x, e)\mid x \in A}\) 与 A 同构
对于任意集合 A 与单元素集合\({e}\)，集合 \({(e, x)\mid x \in A}\) 与 A 同构

所以可以说 Set 是一个幺半范畴

范畴上的幺半群 (Monoid)

前面我们提到的幺半群本质上是一个满足封闭性、结合性以及单位元性质的集合，也就是说幺半群是集合范畴中的一个对象。那么其他范畴是否也存在类似结构的对象呢？答案是肯定的，这就是我们接下来要构造的范畴上的幺半群，它是普通幺半群在范畴意义上的推广。

考虑幺半范畴 \((\mathbb{C}, \otimes,I)\)，以及其中的一个对象 \(M\)，根据幺半范畴的性质，函子 \(\otimes\) 将 \(\mathbb{C}^2\) 中的对象态射到 \(\mathbb{C}\) 中的对象，那么我们不妨设 \(\otimes\) 将 \((M, M)\) 态射到 \(M\)，也就是说存在二元运算 \(\mu: M\otimes M \rightarrow M\)，显然 \(\mu\) 是封闭的。

另一方面，根据幺半范畴的性质，存在自然同构 \(a\) 使得 \((M \otimes M) \otimes M\) 和 \(M\otimes (M \otimes M)\) 同构，这就说明 \(\mu\) 是可结合的。

再假设 \(\mathbb{C}\) 中存在态射 \(\eta: I \rightarrow M\)，以及恒等态射 \(1: M\rightarrow M\)，那么在积范畴 \(\mathbb{C}^2\) 中显然存在态射 \((1, \eta)\) 将 \((I, M)\) 映射到 \((M, M)\)。这种关系再经过函子 \(\otimes\) 映射回 \(\mathbb{C}\) 就可以看作是：\(1 \otimes \eta\) 将 \(I\otimes M\) 映射到 \(M\otimes M\)。也就是如下图所示的关系

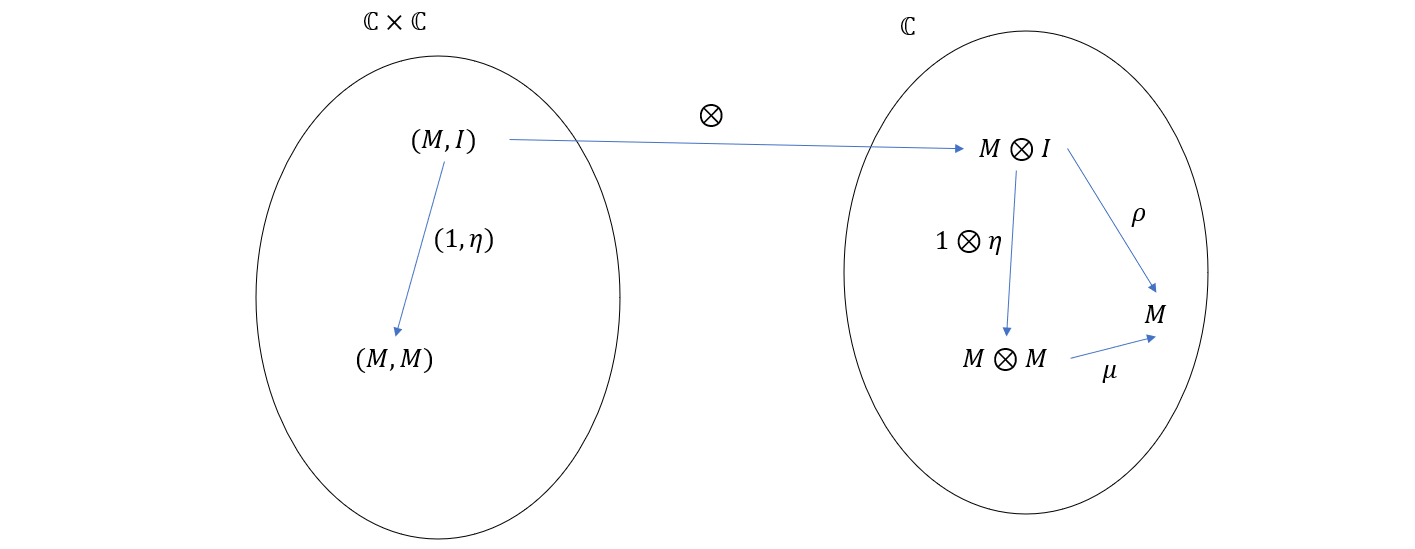
对称地，我们还可以得到如下关系

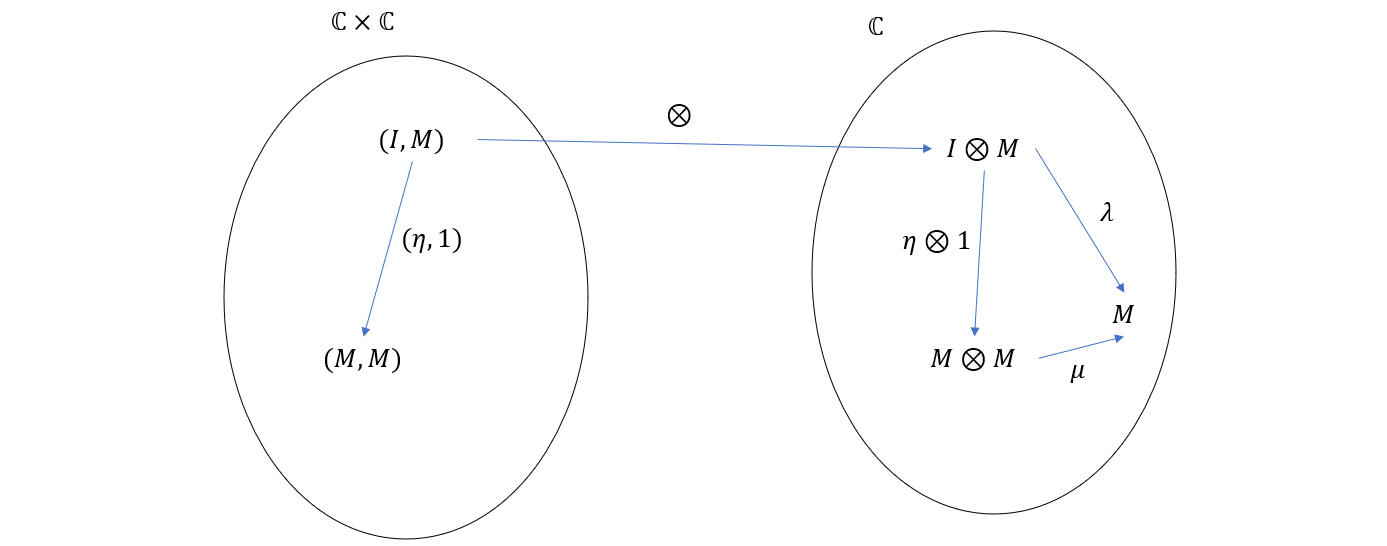
这两张图的右边部分我们可以综合一下，得到下面的交换图

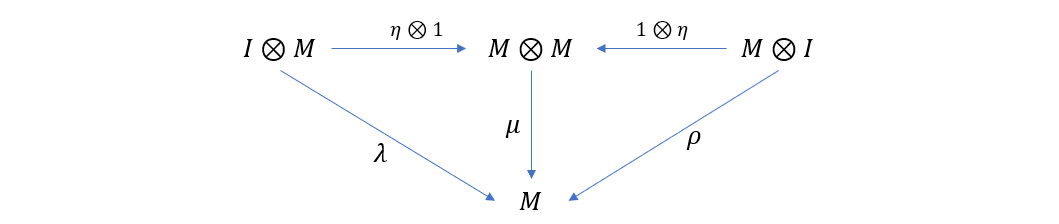
可以看到，态射组合 \(\mu \circ (\eta \otimes 1)\) 等同于 \(\lambda\)，\(\mu \circ (1\otimes \eta)\) 等同于 \(\rho\)，所以 \(\eta\) 可以看作是 \(M\) 在 \(\mu\) 运算下的单位元。

经过以上的讨论，我们可以看到，对象 \(M\) 具有封闭的、可结合的二元运算，以及单位元，因此我们在范畴的意义上构造出了一个幺半群。

函子范畴

设 \(\mathbb{C}\) 是一个小范畴，即\(ob(\mathbb{C})\) 是一个集合，\(\mathbb{D}\) 是任意范畴，则从 \(\mathbb{C}\) 到 \(\mathbb{D}\) 的函子也构成一个范畴，称为函子范畴，标记为 \(Fct(\mathbb{C}, \mathbb{D})\)，它的态射是自然变换。

自函子范畴

若 \(\mathbb{C}\) 是一个小范畴，则从 \(\mathbb{C}\) 到其自身的函子构成自函子范畴，标记为 \(End(\mathbb{C})\)。

自函子范畴上的幺半群 (Monad)

终于，我们来到了 Monad。考虑小范畴 \(\mathbb{C}\)，以及构建在其之上的自函子范畴 \(End(\mathbb{C})\)，它的对象是 \(\mathbb{C}\) 到 \(\mathbb{C}\) 的函子 \(F: \mathbb{C}\rightarrow \mathbb{C}\)，态射是函子之间自然变换 \(n: F \rightarrow G\)。如果以函子组合作为二元运算，以恒等函子作为单位元，则可以证明范畴 \(End(\mathbb{C})\) 是一个幺半范畴。再假设\(End(\mathbb{C})\) 的对象 \(M\) 是一个幺半群，也就是说，满足如下性质：

存在自然变换 \(\mu: M\otimes M \rightarrow M\)，其中 \(\otimes \) 是函子组合运算
存在自然变换 \(\eta: I \rightarrow M\)，其中 \(I\) 是 \(End(\mathbb{C})\) 的单位元，是一个恒等函子。

由于 \(M\) 是一个 \(\mathbb{C}\) 到 \(\mathbb{C}\) 的函子，所以 \(\forall a \in ob(\mathbb{C})\)，被 \(M\) 映射的结果可以用 \(M(a)\) 表示，又由于 \(\otimes\) 是函子组合，所以 \(a\) 又被 \(M\otimes M\) 映射到 \(M(M(a))\)。所以从分量的角度来看，自然变换 \(\mu\) 将 \(M(M(a))\) 映射到了 \(M(a)\)，整个过程如下图所示

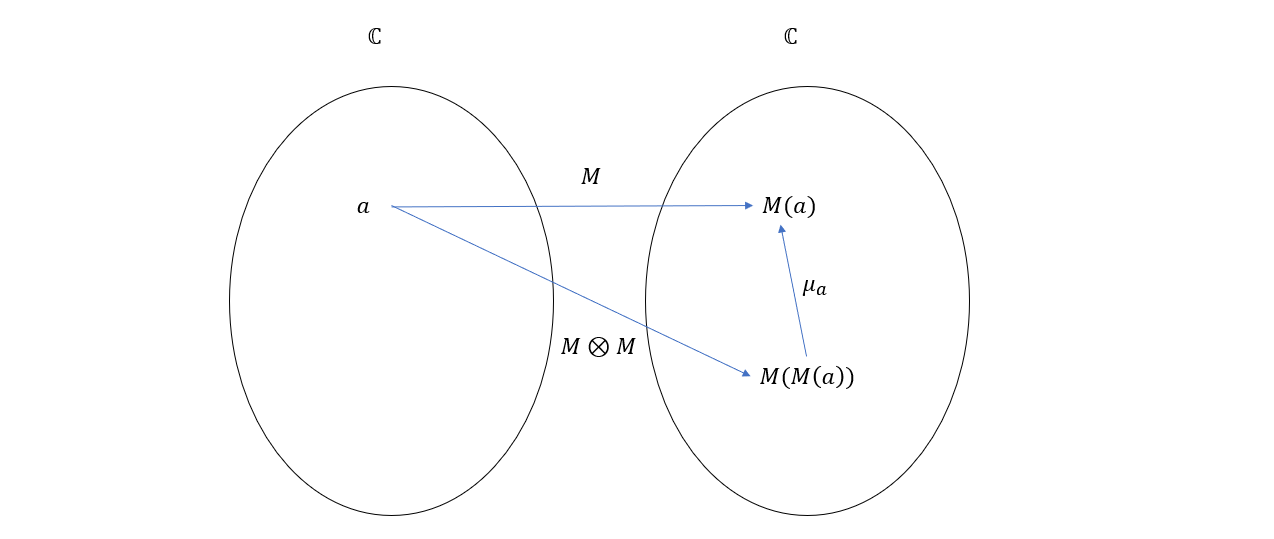
另一方面，从分量的角度看，自然变换 \(\eta\) 把 \(I(a)\) 映射到了 \(M(a)\)，而由于 \(I\) 是恒等函子，所以 \(I(a) = a\)，整个过程如下图所示

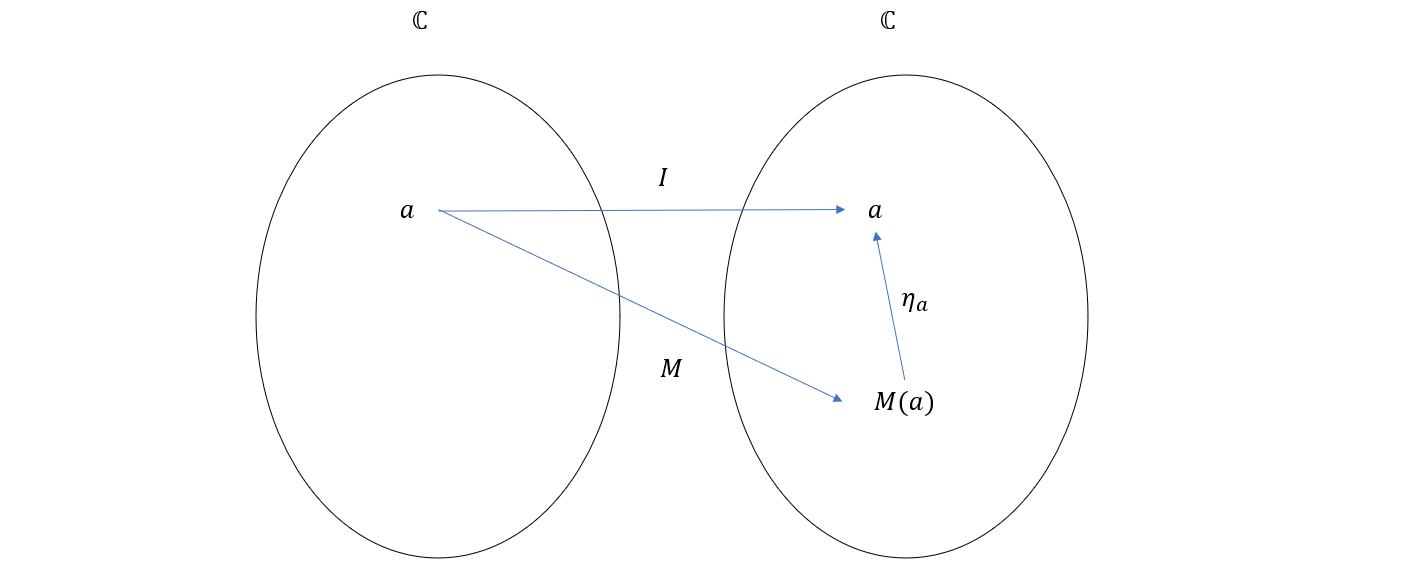
上面两幅图就向我们展示了 \(M\) 的两个基本操作

\[\begin{aligned} &\mu: M(M(a)) \rightarrow M(a)\\ &\eta: a \rightarrow M(a) \end{aligned}\]

其中 \(\mu\) 和 \(\eta\) 就是我们在 Haskell 中见到的 return 和 join，使用 join 和 fmap，我们还可以构造出 bind 操作，即著名的 >>=

(>>=) :: m a -> (a -> m b) -> m b

首先我们看到

fmap (a -> m b) (m a) = m (m b)

然后只需要应用 join 就可以得到 m b 了，

join (m (m b)) = m b

也就是说

>>= = join . fmap

经过以上讨论，我们发现这其实就是 Haskell 中 Monad 的性质，所以说 Monad 是自函子上的幺半群就不难理解了。