批量正则化的前馈计算与反向传播分析
Batch Normalization 想要解决什么问题?
很多时候,当我们训练好一个模型,拿到实际运行环境中会发现精度表现不如预期,其中有一个可能的原因是实际环境中的数据分布和我们训练集的分布不同,术语叫 Covariate Shift。这时我们可以采用一些办法把真实数据的分布变换成想要的形式,比如标准化,对数变换等等。在神经网络训练过程中,每一层的输入数据都经过了前面多层处理,并且每层的权重参数都在反向传播的过程中不断变化,因此,即便同样的初始数据在不同轮次的训练中都可能有不同的分布,这一现象也被称为 Internal Covariate Shift。既然数据分布都不一样了,那上一批次训练的参数可能就失效了,这就迫使每层的权重参数不断地修正自己来适应新的数据分布,而不是朝着减小损失函数的方向,从而导致模型难以收敛。另一方面,以 sigmoid 激活函数为例 \(f(x) = \frac{1}{1 + e^{-x}}\),它的导数形式为 \(\frac{e^{-x}}{(1+e^{-x})^2}\),如果把导数的图像画出来,大致如下所示
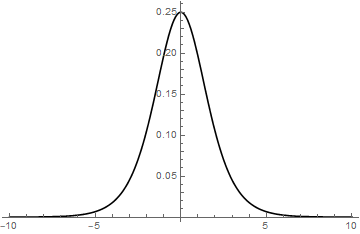
可以看到,当 x 的绝对值很大的时候,sigmoid 函数的梯度值接近于 0,也就是说梯度消失了。一种比较理想的情况是输入张量的每个分量的绝对值都位于 0 附近。但是正因为 Internal Covariate Shift 的存在,输入张量值不可能稳定地保持在 0 左右。
通过以上分析可以看到,Internal Covariate Shift 主要造成了两个问题,一个是拖慢模型收敛速度,另一个是在某些激活函数上的梯度消失。为了解决这些问题,论文作者提出的方法是对每个批次的数据强制修改其分布到统一的形式,也就是 Batch Normalization。从今天的视角来看,尽管有论文认为 BN 并没有解决 Internal Covariate Shift 问题,但 BN 的效果无疑是值得肯定的,几乎已经成为了神经网络模型的标配结构。
Batch Normalization 的具体计算方法
设一个 batch_size 等于 m 的小批量 \(\mathcal{B} = {x_1, x_2, …x_m}\),其中每个数据的维度都为 d,整体上来看,该批量数据的均值和方差分量分别为
这里的 \(\epsilon\) 是一个极小量,它的作用是为了避免当所有 \(x_i\) 都相同时的零方差情况。为了把数据变换到均值为0,方差为1 的分布,我们对每个样本的每个分量做如下计算
\[\hat{x}_{i}^{(k)} = \frac{x_i^{(k)} - \mu^{(k)}}{\sigma^{(k)}} \qquad \qquad (3)\]忽略 \(\epsilon\) 的情况下,这时的 \(\hat{x}_i\) 服从标准的正态分布,但我们无法确定这是使得模型效果最佳的分布,因此,最后再添加一个可训练的线性变换
\[y_i^{(k)} = \gamma^{(k)} \hat{x}_{i}^{(k)} + \beta^{(k)} \qquad \qquad (4)\]其中 \(\beta^{(k)}, \gamma^{(k)}\) 都是可训练参数。这样一来,每个 BN 层都能学到一个最佳的数据分布,从而增强模型的表现能力。
Batch Normalization 的反向传播
BN 层的计算图依赖可以简单表示如下
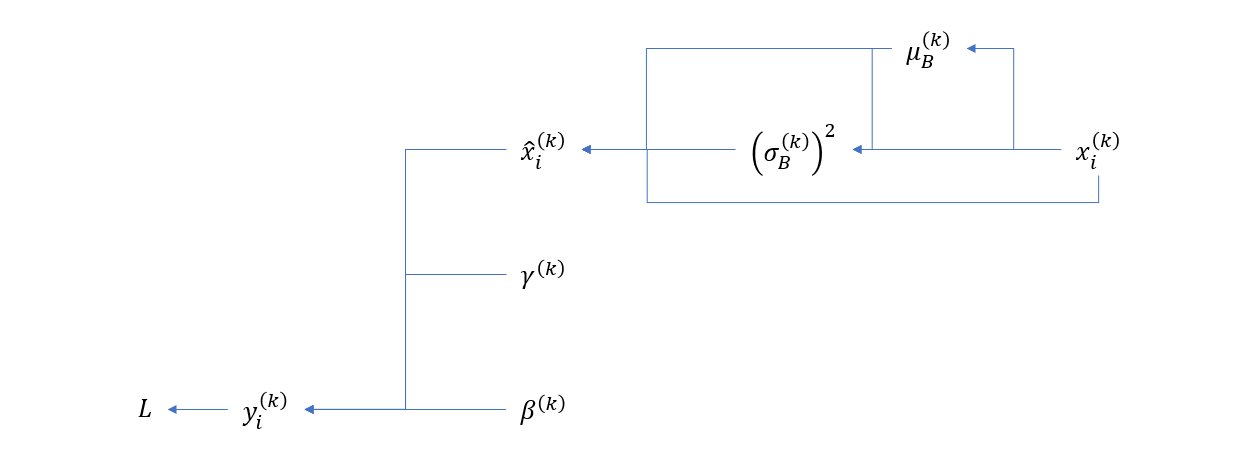
因此,我们需要计算如下导数
\[\frac{\partial L}{\partial \gamma^{(k)}}, \frac{\partial L}{\partial \beta^{(k)}}, \frac{\partial L}{\partial x_i^{(k)}}\]根据复合函数的求导规则,又有以下公式
\[\begin{aligned} \frac{\partial L}{\partial \gamma^{(k)}} &= \sum_{i=1}^m \frac{\partial L}{\partial y_i^{(k)}} \frac{\partial y_i^{(k)}}{\partial \gamma^{(k)}} \qquad \qquad (5)\\ \frac{\partial L}{\partial \beta^{(k)}} &= \sum_{i=1}^m \frac{\partial L}{\partial y_i^{(k)}} \frac{\partial y_i^{(k)}}{\partial \beta^{(k)}} \qquad \qquad (6)\\ \frac{\partial L}{\partial x_i^{(k)}} &= \frac{\partial L}{\partial \hat{x} _i^{(k)}} \frac{\partial \hat{x}_i^{(k)}}{\partial x_i^{(k)}} + \frac{\partial L}{\partial (\sigma^{(k)})^2} \frac{\partial (\sigma^{(k)})^2}{\partial x_i^{(k)}} + \frac{\partial L}{\partial \mu^{(k)}} \frac{\partial \mu^{(k)}}{\partial x_i^{(k)}} \qquad \qquad (7) \end{aligned}\]根据公式 (4)
\[y_i^{(k)} = \gamma^{(k)} \hat{x}_{i}^{(k)} + \beta^{(k)}\]可得
\[\begin{aligned} \frac{\partial y_i^{(k)}}{\partial \gamma^{(k)}} &= \hat{x}_{i}^{(k)} \\ \frac{\partial y_i^{(k)}}{\partial \beta^{(k)}} &= 1 \end{aligned}\]于是
\[\begin{aligned} \frac{\partial L}{\partial \gamma^{(k)}} &= \sum_{i=1}^m \frac{\partial L}{\partial y_i^{(k)}} \hat{x}_{i}^{(k)} \\ \frac{\partial L}{\partial \beta^{(k)}} &= \sum_{i=1}^m \frac{\partial L}{\partial y_i^{(k)}} \end{aligned}\]对于公式 (7) 来说,我们逐项推导如下
\[\begin{aligned} \frac{\partial L}{\partial \hat{x}_i^{(k)}} &= \frac{\partial L}{\partial y_i^{(k)}} \frac{\partial y_i^{(k)}} {\partial \hat{x}_i^{(k)}} = \frac{\partial L}{\partial y_i^{(k)}} \gamma^{(k)}\\ \frac{\partial \hat{x}_i^{(k)}}{\partial x_i^{(k)}} &= \frac{1}{\sigma^{(k)}}\\ \frac{\partial L}{\partial (\sigma^{(k)})^2} &=\sum_{i=1}^m \frac{\partial L}{\partial \hat{x}_i^{(k)}} \frac{\partial \hat{x}_i^{(k)}}{\partial \sigma^{(k)}} \frac{\partial \partial \sigma^{(k)}}{\partial (\sigma^{(k)})^2} = \sum_{i=1}^m\frac{\partial L}{\partial \hat{x}_i^{(k)}} \cdot \left(-\frac{x_i^{(k)} - u_B^{(k)}}{2 (\sigma^{(k)})^3}\right)\\ \frac{\partial (\sigma^{(k)})^2}{\partial x_i^{(k)}} &= \frac 2 m (x_i^{(k)} - \mu^{(k)}) \\ \frac{\partial L}{\partial \mu^{(k)}} &= \sum_{i=1}^m\frac{\partial L}{\partial \hat{x}_i^{(k)}} \frac{\partial \hat{x}_i^{(k)}}{\partial \mu^{(k)}} + \frac{\partial L}{\partial (\sigma^{(k)})^2} \frac{\partial (\sigma^{(k)})^2}{\partial \mu^{(k)}} = \sum_{i=1}^m\frac{\partial L}{\partial \hat{x}_i^{(k)}} \left(-\frac{1}{\sigma^{(k)}}\right) + \frac{\partial L}{\partial (\sigma^{(k)})^2} \left(- \frac 2 m \sum_{i=1}^m(x_i^{(k)} - \mu^{(k)}) \right) \\ \frac{\partial \mu^{(k)}}{\partial x_i^{(k)}} &= \frac 1 m \end{aligned}\]综合一下,将上面 6 个公式代入公式 (7) 就可以得到最终结果,但那样公式太长,我们这里就懒得写了。