使用CUDA实现一个简单的矩阵乘法

矩阵乘法可以说是高性能计算领域的新手村问题，同时也是很多重要应用的基石，它的基本算法相当简单，但是为了达到令人满意的速度，却需要花费相当大的精力来优化。下面，我们从最简单的实现开始

// VERSION 1
// A, B, C are all matrices
// M, N are the dimensions C, and K is the columns of A and rows of B
for (int i = 0; i < M; i++) {
    for (int j = 0; j < N; j++) {
        for (int k = 0; k < K; k++) {
            C[i * N + j] += A[i * K + k] * B[k * N + j];
        }
    }
}

这里指标 i 沿着 A 的行方向，j 沿着 B 的列方向移动，而 k 同时沿着 A 的列方向和 B 的行方向移动。这是一个三层循环，最内层那行代码实际运行了 M x N x K 次，所以这是一个时间复杂度达到 (\mathcal{O}(n^3)) 的算法。

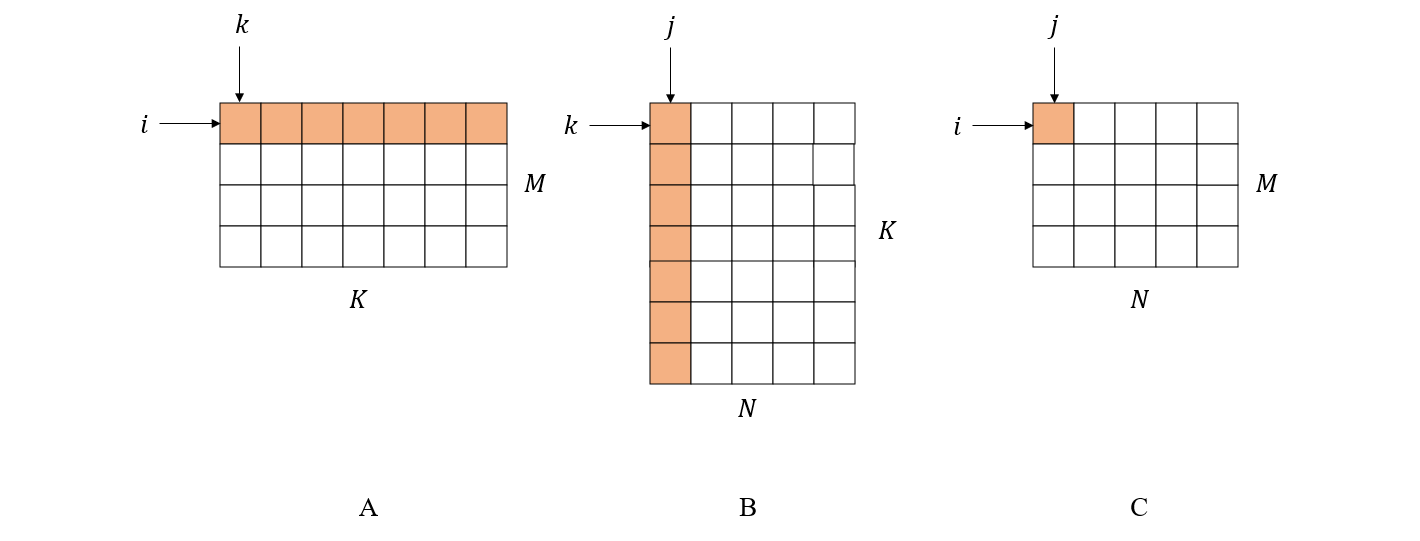
一个常见的优化方法是调整矩阵遍历方式。我们知道现代计算机的分级存储模型，从 CPU 寄存器到一级缓存、二级缓存、三级缓存、内存、硬盘直到分布式存储系统，容量越来越大，速度越则是按量级递减。当矩阵被读入内存后，CPU 不会一个元素一个元素地访问，而是一条指令带走一批连续存储的数据块到自己的缓存上，这样在访问下一个元素的时候不用再到内存里面寻址，节省了不少时间。假设我们用的 row-major 存储，那么矩阵在行方向上是连续存储的，这就导致 CPU 在访问矩阵 A 的时候大部分时间都是在缓存中访问，因为指标 i 是在 A 的行方向遍历，而访问矩阵 B 就可能会经常缓存命中失败（特别是对于大矩阵）。所以如果能把对 B 的遍历方式改成也是按行方向进行，那么就可以在理论时间复杂度不变的情况下，节省不少寻址的时间。

把对 B 的访问改成行方向进行，这里我们暂时可以想到两种方法，第一种是把矩阵 B 整个转置，它的额外成本在于矩阵转置的消耗。

// VERRSION 2
// BT is the transpose of B
for(int i = 0; i < M; i++) {
    for (int j = 0; j < N; j++) {
        for (int k = 0; k < K; k++) {
            C[i * N + j] += A[i * K + k] * BT[j * K + k];
        }
    }
}

而第二种方法则不对 B 做任何调整，而是每次计算 C 中元素的一部分。具体来说，在 VERSION 1 的代码中，最内层循环会完整地计算 C 中的一个元素，这需要完全遍历 A 的一行和 B 的一列，现在不让在列方向上访问 B 了，那么就只能得到 C 中每个元素的一部分，先存在对应位置上，接着计算下一个元素。体现在代码中，其实就是交换了 k 和 j 的循环顺序

// VERSION 3
for(int i = 0; i < M; i++) {
    for(int k = 0; k < K; k++) {
        for(int j = 0; j < N; j++) {
            C[i * N + j] += A[i * K + k] * B[k * N + j];
        }
    }
}

以上这两种方法都能解决 B 的列遍历问题，但是究竟哪一种的时间消耗更小还不得而知，有兴趣的同学可以自己实验一下。

接下来我们考虑如何在并行环境中实现矩阵乘法。并行计算的意思其实就是在同一时刻完成多个计算操作，在计算机上，完成这个操作的主体就是 CPU 核心，不严谨的讲，比如 CPU 有8核的，16核的，就代表这个CPU可以同时执行 8 个或者 16 个操作，而 GPU 则更不得了，可以同时完成成千上万个操作。现在假设我们有无数个核心可以利用，那么是否任何计算都可以在一个操作的时间内完成呢？以矩阵乘法为例，我们把其中的每个数学运算都分配给一个独立的核心，就可以发现，从 A 中取数据这个操作不能和运算 (i * K + k) 同时进行，所以上述问题的答案是否定的。另一方面，C 中的每个元素是否可以单独分配给一个核心来计算呢？这当然没问题，因为 C 中元素本身就互不影响，它们都可以看作是由两个向量点积得到的。

实际上，并行计算有一套完整的理论基础，简单来说，如果把一个计算任务分解成若干个独立的小任务，这些小任务的执行顺序不影响最终结果，则它们就可以并行执行。显然，在矩阵乘法问题中，先计算 C 中的哪个元素并不影响最终得到的矩阵，所以关于 C 的元素的计算是可以并行化的。

C 中元素的计算过程其实就是 VERSION 1 代码中的最内层循环，现在，假如我们有大于 M * N 个核心，则可以把每个内层循环都分配给一个独立的核心，然后把结果填充到 C 中即可。这样一来，原本需要 M * N 个时间单位的消耗就变成了一个单位的时间消耗，理论速度提升了 M * N 倍。

在 CUDA 中，计算核心被抽象成了 thread，多个 thread 可以被组织成 block，一个 block 最多可以有 3 个维度，由 blockDim.x, blockDim.y 和 blockDim.z 这三个内置变量来表示，而 thread 在 block 中的位置则用 threadIdx.x, threadIdx.y 和 threadIdx.z 表示。

在 block 之上，还有一个 grid 结构，同 thread 与 block 的关系类似，grid 的维度由 gridDim.x, gridDim.y 和 gridDim.z 表示，block 在 grid 中的位置则由 blockIdx.x, blockIdx.y 和 blockIdx.z 表示。所以，一个 grid 的完全体就是一个三维的 block 块，如下图所示

使用 thread 来抽象计算核心的一大功效是屏蔽掉了不同硬件物理核心的细节差异，从而更减少开发者的心智负担。可以设想一下，如果让开发者直接把任务分配到物理核心上，那么大家就会思考怎样去编写适应不同硬件设备的程序。有的设备核心少，不能一次性把任务执行完，而需要分批次运行，而有的设备核心多，一次就搞定了。这样一来就很难开发通用的程序了。而使用 thread 来作为物理核心和开发者之间的桥梁，大家只管申请 thread 数量，然后由 thread 控制程序来决定如何把 thread 分配到物理核心上，核心多就并行度高，核心少就并行度低，不用开发者自己来理这个事情。

接下来我们来实际看一下 CUDA 版本的矩阵乘法，由于 CPU 和 GPU 是两种不同的硬件，它们都有各自的内存设备，我们首先在 GPU 上申请内存空间

float *dA = NULL, *dB = NULL, *dC = NULL;
cudaMalloc(&dA, sizeA);
cudaMalloc(&dB, sizeB);
cudaMalloc(&dC, sizeC);

然后把 CPU 上的矩阵拷贝到 GPU 上

cudaMemcpy(dA, hA, sizeA, cudaMemcpyHostToDevice);
cudaMemcpy(dB, hB, sizeB, cudaMemcpyHostToDevice);

再接下来我们考虑 GPU 上的 thread 分配问题，由于每个 thread 负责计算 C 中的一个元素，所以最直观的方法是申请一个 M x N 大小的 block，让 C 中的每个元素和 block 中的 thread 一一对应。编写 GPU 端的代码如下（使用 __global__ 关键字修饰的函数）

// VERSION 4
__global__ void matrixMul(float* A, float* B, float* C, int M, int N, int K){

    int nRow = threadIdx.x;
    int nCol = threadIdx.y;

    for(int i = 0; i < K; i++) {
        C[nRow * N + nCol] += A[K * nRow + i] * B[N * i + nCol];
    }

}

这个函数会在每个 thread 上都执行一次，所以要使用 threadIdx 来确定当前 thread 应该计算的任务，PS. 我觉得这是理解并行计算编程最关键的知识点。由于 C 和 block 中的 thread 一一对应，所以这里我们用 threadIdx.x 来表示 C 的行索引，threadIdx.y 来表示 C 的列索引，剩下的部分就没什么好说的了。

最后，我们再回到 CPU 端看看调用方

int gridSize=1;
dim3 blockSize(M, N);

matrixMul<<<gridSize, blockSize>>>(dA, dB, dC, M, N, K);
cudaDeviceSynchronize();
cudaMemcpy(hC, dC, sizeC, cudaMemcpyDeviceToHost);

这里我们将 gridSize 设为 1，也就是说 grid 是一个 1 x 1 x 1 的结构，然后是前面多次提到的 M x N 的 block。在调用 GPU 端函数的时候，需要按一定的格式传参数，后面的 cudaDeviceSynchronize() 是等待 GPU 端执行完成，最后再将显存中的结果拷贝到 CPU 端即可。

以上就是最基础的 CUDA 版矩阵乘法，其中还有很大的优化余地，我们将在以后的文章中讨论。