算法题:矩形分割
问题 给定一个矩形框作为背景,在其中放置一个方块,可以将大矩形分割成若干个大小不等的矩形区域,放置的方块越多,分割方案也越多,如下图所示。
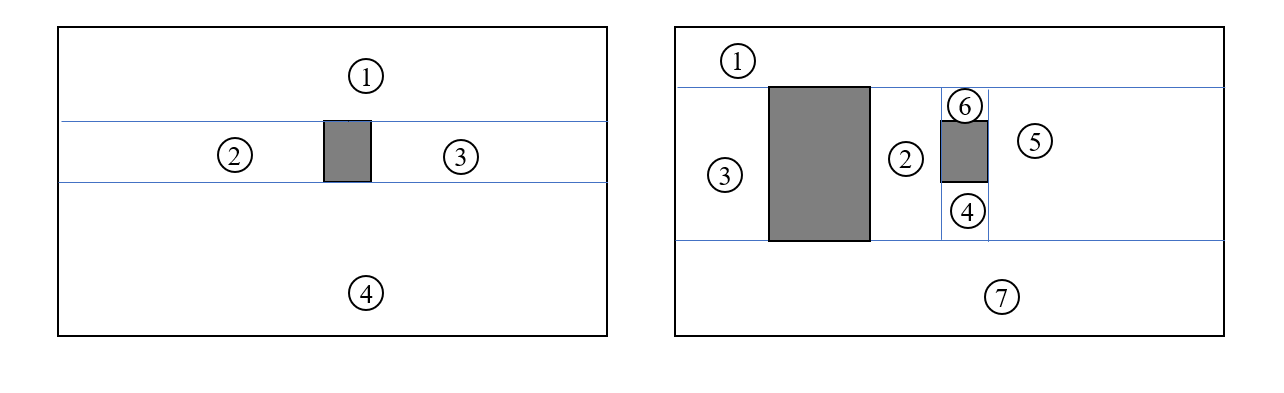
现在给出大矩形的坐标,以及若干方块的坐标(方块完全位于大矩形内部,且它们之间不相交,并且放置顺序固定),要求编程输出分割后最大的矩形区域坐标。
思路
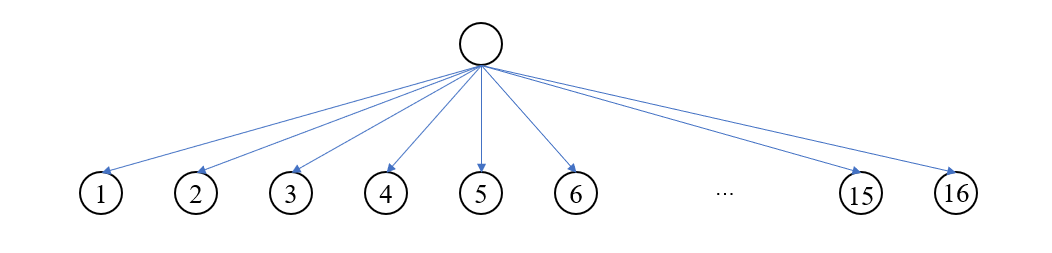
首先分析放置一个矩形的分割情况,一个方块可以把背景分割成 4 个矩形区域,其中每个点可以横向或者纵向绘制线段,因此总共有 (2^4 = 16) 种分割方案。
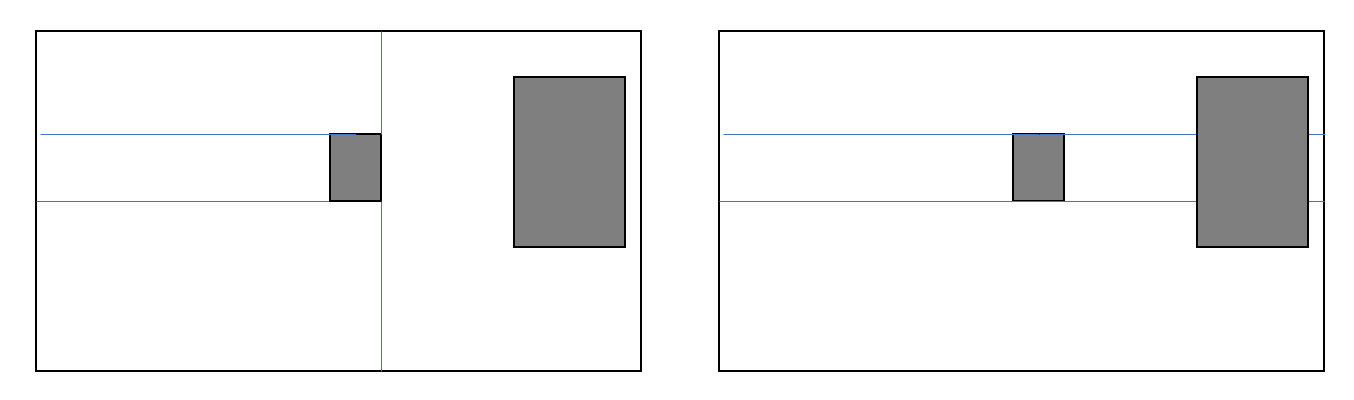
在放置第二个矩形物体的时候,会出现两种情况,一种情况是落入前一步的小矩形内(下图左边),第二情况是破坏原来的分割方案(下图右边)。
对于第一种情况,置入的物体可以继续分割其所在的矩形,而第二种情况则直接淘汰掉,表现在树结构上可以看作是剪枝
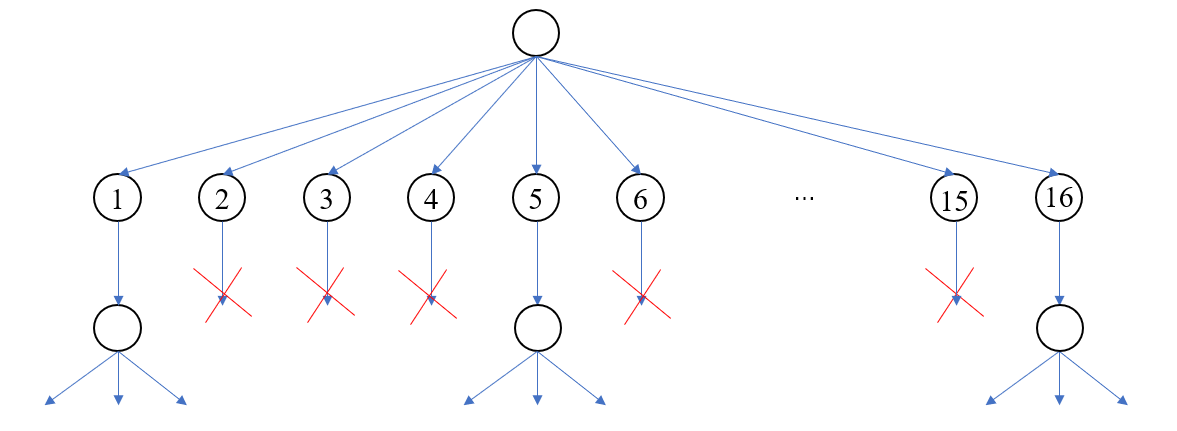
加入更多的物体其实就是不断的对树进行扩展,并在这一过程中剪枝。最终可以得到多条可行的路径,每条路径都是一个可行的分割方案,我们只需追溯这些路径就可以看到方块对背景的分割情况,选择一个拥有最大矩形子区域的方案即可。
下面我们采用动态规划的方法来描述解决方案: 原问题:给定一个矩形,以及 n 个矩形方块,求解方块对矩形的所有分割方案; 终止解:给定一个矩形,以及一个方块,可以把矩形分割成4个矩形区域,且共有16种方案; 递归问题:已知一个矩形,以及 n - 1 个方块对其进行分割的所有方案,求解再添加一个方块得到的所有切割方案。
实现
首先,我们实现一个函数,其目的是计算一个方块对矩形的一种分割方案
/**
* 矩形被方块分割成 4 个矩形
* @param rect 背景矩形坐标
* @param obj 方块坐标
* @param axisDirection 方块四个点的分割方向,0代表横向,1代表纵向
* @return 四个子区域的坐标
* */
public static List<int[]> splitRect(int[] rect, int[] obj, int[] axisDirection) {
int left = 0;
int right = 1;
int top = 2;
int bottom = 3;
int l = rect[left];
int r = rect[right];
int t = rect[top];
int b = rect[bottom];
int ol = obj[left];
int or = obj[right];
int ot = obj[top];
int ob = obj[bottom];
int[][] rects = new int[4][4];
rects[0] = new int[]{l, ol, t, b};
rects[1] = new int[]{l, r, t, ot};
rects[2] = new int[]{or, r, t, b};
rects[3] = new int[]{l, r, ob, b};
if(axisDirection[0] == 0) {
rects[0][top] = obj[top];
rects[1][bottom] = obj[top];
}else {
rects[0][right] = obj[left];
rects[1][left] = obj[left];
}
if(axisDirection[1] == 0) {
rects[1][bottom] = obj[top];
rects[2][top] = obj[top];
}else {
rects[1][right] = obj[right];
rects[2][left] = obj[right];
}
if(axisDirection[2] == 0) {
rects[2][bottom] = obj[bottom];
rects[3][top] = obj[bottom];
}else{
rects[2][left] = obj[right];
rects[3][right] = obj[right];
}
if(axisDirection[3] == 0) {
rects[0][bottom] = obj[bottom];
rects[3][top] = obj[bottom];
} else {
rects[0][right] = obj[left];
rects[3][left] = obj[left];
}
return Arrays.asList(rects);
}
这里的 axisDirection 参数规定了方块四个角点的分割线方向,当其都为 0 的时,即都横向分割,那么获得的分割矩形形如下图

前面我们提到,一个方块可以有 16 种分割方案,其中每种方案就是由这里的 axisDirection 完全确定的,为了呈现所有分割方案,我们需要列出所有可能的 axisDirection 值,即 0 和 1 构成的四元素数组的全排列
/**
* 给定数字 0...n-1,求由这些数字组成长度为 len 的数组的全排列
* 终止解:给定数字 0...n-1,由这些数字组成长度为 1 的数组的全部情况为 [0], [1], ... [n-1]
* 递归问题:给定数字 0...n-1,以及由这些数字组成长度为 len - 1 的数组的全排列,求由这些数字组成长度为 len 的数组的全排列
* */
public static List<List<Integer>> permutation(int len, int n) {
// 终止条件
if(len == 1) { // 构造列表 [[0], [1], ... [n-1]]
ArrayList<List<Integer>> list = new ArrayList<>();
for (int i = 0; i < n; i++) {
ArrayList<Integer> ls = new ArrayList<>();
ls.add(i);
list.add(ls);
}
return list;
}
// 递归求解子问题
List<List<Integer>> list = permutation(len - 1, n);
return list.stream()
.flatMap(ls -> {
ArrayList<List<Integer>> lists = new ArrayList<>();
for (int i = 0; i < n; i++) {
ArrayList<Integer> ls2 = new ArrayList<>(ls);
ls2.add(i);
lists.add(ls2);
}
return lists.stream();
})
.collect(Collectors.toList());
}
下面我们在实现两个工具函数,用于判断矩形之间的关系
/**
* 判断两个矩形是否有交集
* 如果某一个矩形的左边大于另一个矩形的右边,或某矩形的上边小于另一矩形的下边,则两者不相交,否则相交
* */
def isRectOverlap(rect1: Array[Int], rect2: Array[Int]): Boolean = {
!(rect1(0) > rect2(1) || rect1(1) < rect2(0) || rect1(2) > rect2(3) || rect1(3) < rect2(2))
}
/**
* 判断两个矩形是否是包含关系
*
* @param rect1 外部矩形
* @param rect2 内部矩形
* */
def isRectContains(rect1: Array[Int], rect2: Array[Int]): Boolean = {
rect1(0) < rect2(0) && rect1(1) > rect2(1) && rect1(2) < rect2(2) && rect1(3) > rect2(3)
}
最后,我们实现多个方块分割方案函数
/**
* 给定一个矩形,以及 n 个方块,求解对矩形的所有分割方案
* 终止解:给定一个矩形,以及一个方块,可以把矩形分割成4个小矩形区域,且共有16种方案
* 递归问题:已知一个矩形,以及 n - 1 个方块对其进行分割的所有方案,求解再添加一个方块得到的所有切割方案
* @param rect 被分割矩形
* @param objs 方块列表
* */
public static List<List<int[]>> splitRect(int[] rect, List<int[]> objs) {
if(objs.isEmpty()) {
ArrayList<List<int[]>> lists = new ArrayList<>();
ArrayList<int[]> list = new ArrayList<>();
list.add(rect);
lists.add(list);
return lists;
}
if(objs.size() == 1) {
return splitRect(rect, objs.get(0));
}
int[] obj = objs.remove(0);
// 求解子问题
List<List<int[]>> plans = splitRect(rect, objs);
// 向目前的分割方案中添加一个方块
return plans.stream()
.flatMap(plan -> {
// 判断当前方块是否与现有区域相交
boolean intersect = plan.stream()
.anyMatch(rt -> isRectOverlap(rt, obj) && !isRectContains(rt, obj));
if(intersect) {
return Stream.empty();
}
// 找到包含当前方块的区域,用于后续分割
Optional<int[]> contains = plan.stream()
.filter(rt -> isRectContains(rt, obj))
.findFirst();
if(!contains.isPresent()) {
return Stream.empty();
}
// 不包含当前方块的区域列表
List<int[]> plan2 = plan.stream()
.filter(rt -> !isRectContains(rt, obj))
.collect(Collectors.toList());
int[] rt = contains.get();
return splitRect(rt, obj)
.stream()
.map(list -> {
List<int[]> newPlan = new ArrayList<>(plan2);
newPlan.addAll(list);
return newPlan;
});
})
.filter(list -> !list.isEmpty())
.collect(Collectors.toList());
}
至此,我们实现了列举多个方块分割背景矩形的所有方案的算法。测试一下
ArrayList<int[]> objs = new ArrayList<>();
int[] r1 = {150, 250, 150, 250};
objs.add(r1);
int[] r2 = {300, 350, 180, 300};
objs.add(r2);
List<List<int[]>> lists = splitRect(new int[]{100, 800, 100, 600}, objs);
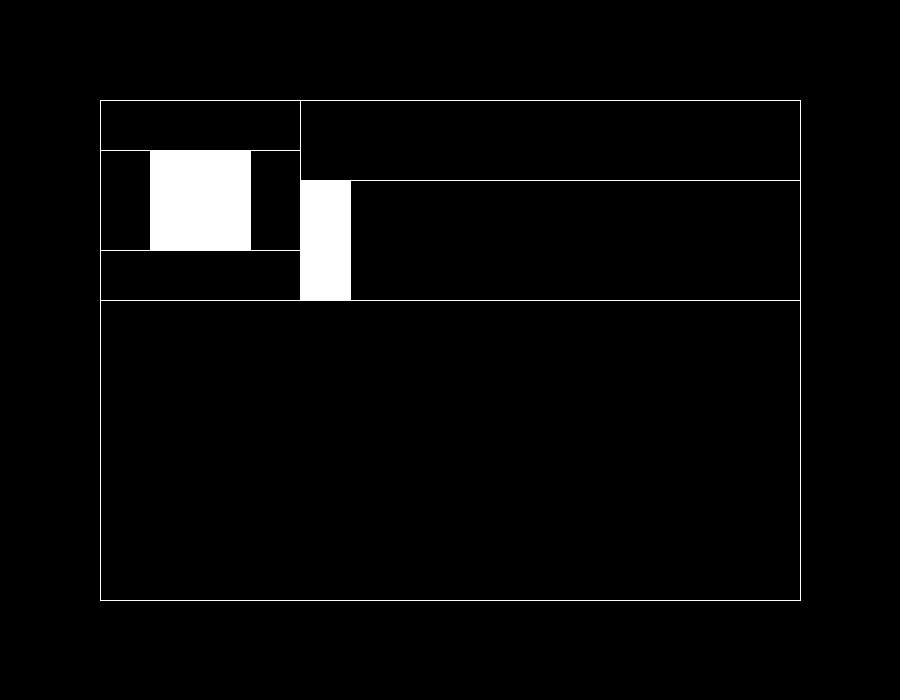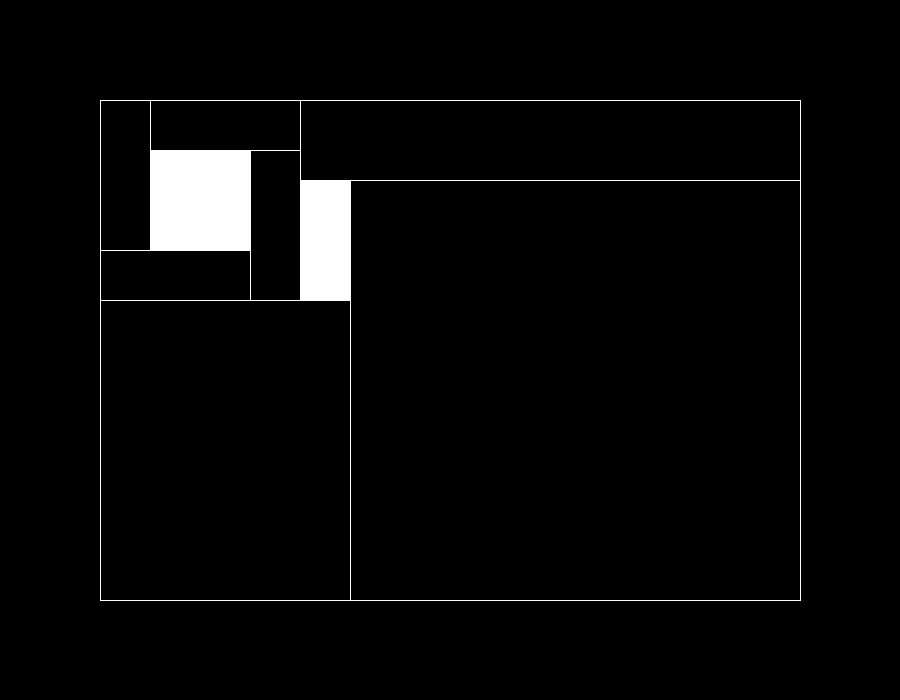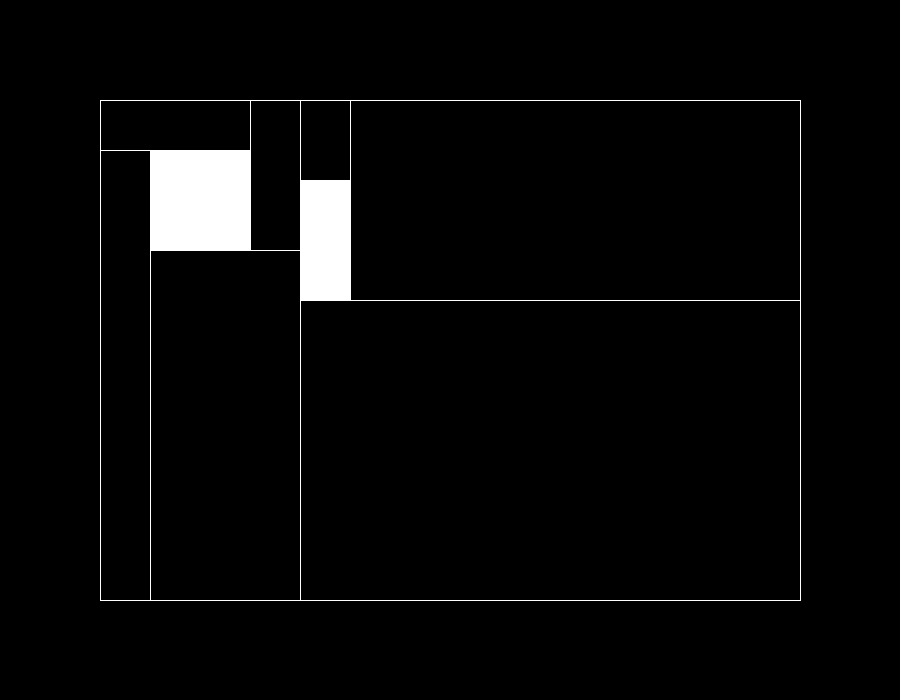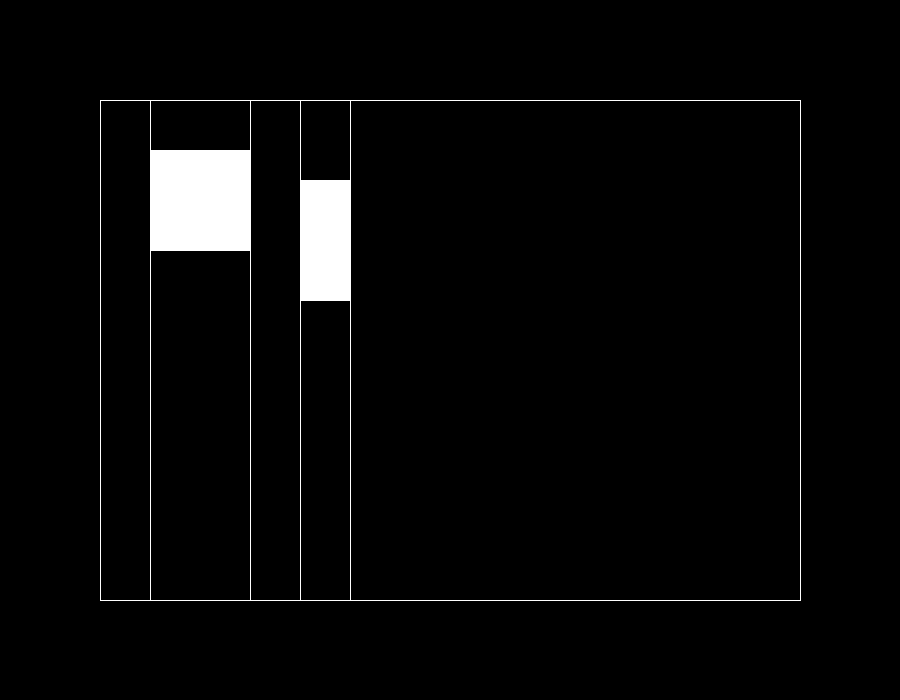
要解决最初的问题,只需要找到这些方案中面积最大的子区域即可。