人脸姿态估计 (1)

人脸姿态估计指的是根据一幅2维的人脸图像，计算出这个人在实际3维空间中的面部朝向。问题的输入条件就是一张人脸图片，输出自然就是可以表示方位的三个旋转角度 (pitch, yaw, roll)，其中 pitch 表示俯仰角（关于x轴的旋转角度），yaw 表示偏航角（关于y轴的旋转角度），roll 表示翻滚角（关于z轴的旋转角度），分别如下面 3 图所示：(说句题外话，如果我们把下面图中的物体看作是一架向我们飞来的飞机，就可以理解为何这三个角要如此命名了)

算法的思路很简单，可以考虑这样一种场景，假设我们有一张标准的3d人脸模型，如果投影和输入图片的人脸大致重合，那么此时 3d 模型的方位就可以看作是图片中人脸在实际空间中的方位了。如果投影和图像的差异很大，那我们再对 3d 模型进行旋转，平移，拉伸等操作，可以明确的是，只要经过合适的调整，总会出现两者相重合的情况。

所以现在的问题就变成了三个子问题：1. 怎样得到标准的人脸 3d 模型；2. 对 3d 模型的各种变换操作怎样从数字上体现出来；2. 如何量化的表示“重合”这一概念。

我们先来看第二个问题，在数学上，旋转、平移、拉伸操作其实都是矩阵运算，举个简单的例子，在二维平面上旋转一条线段，就是使用旋转目标 src 去乘以二维旋转矩阵，得到的 dst 便是旋转后的线段。

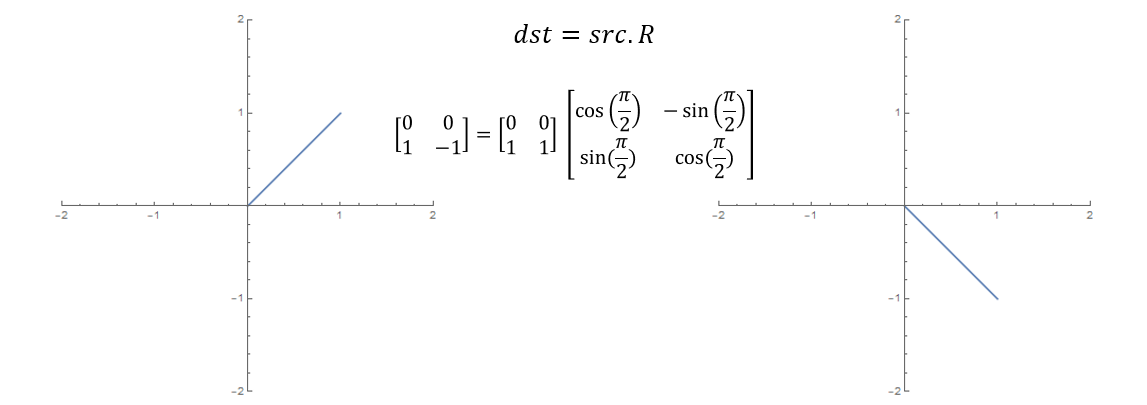
平移操作更简单一点，在坐标分量上加一个偏移量即可。拉伸也同理，只需要在不同的方向上乘以缩放系数。于是，空间中的一个对象，经过上述变换后，最终得到的东西由下式给出

\[dst = (src \cdot R + t)\cdot s\]

其中 \(t\) 是平移矩阵，大小为 \(n\times 3\)，它的每一列数值为常量，是对应方向上的移动距离

\[t=\left[ \begin{aligned} &dx &dy\quad&dz\\ &dx &dy\quad&dz\\ &dx &dy\quad&dz\\ &...& ... \quad &... \end{aligned} \right]\]

\(s\) 是缩放向量，具体形式为

\[s=\left[ \begin{aligned} \lambda_x \quad 0\quad 0\\ 0\quad \lambda_y\quad 0\\ 0\quad 0\quad \lambda_z \end{aligned} \right]\]

这里的 \(\lambda_x, \lambda_y,\lambda_z\) 是三个方向上的缩放系数。

下面我们重点讨论一下旋转矩阵 \(R\) 的形式，与二维情况不同的是，三维旋转有三个旋转轴，针对每一个旋转轴都有一个旋转矩阵形式，具体来说

\[R_x=\left[ \begin{aligned} &1 &0&\quad 0\\ &0 &\cos(\alpha) &\quad-sin(\alpha)\\ &0 &\sin(\alpha) &\quad \cos(\alpha) \end{aligned} \right]\] \[R_y=\left[ \begin{aligned} &\cos(\beta) &0&\quad -sin(\beta)\\ &0 &1 &\quad0\\ &\sin(\beta) &0 &\quad \cos(\beta) \end{aligned} \right]\] \[R_z=\left[ \begin{aligned} &\cos(\gamma) &-sin(\gamma)&\quad 0\\ &\sin(\gamma) &\cos(\gamma) &\quad 0\\ &0 &0 &\quad 1\quad \end{aligned} \right]\]

其中 \(\alpha, \beta,\gamma\) 分别是关于 \(x,y,z\) 轴的旋转角度，最终的旋转矩阵是上述这三个矩阵相乘之积

\[R = R_x R_y R_z\]

于是经过变换后的模型就是 \(\alpha, \beta, \gamma, \lambda_x, \lambda_y, \lambda_z, dx, dy, dz\) 这些变量的函数

\[dst(\alpha, \beta, \gamma, \lambda_x, \lambda_y, \lambda_z, dx, dy, dz) = (src \cdot R + t)\cdot s\]

搞定了标准 3d 人脸模型的变换之后，接下来我们来解决如何量化投影与人脸图像重叠的问题。由于 3d 模型其实就是一系列点坐标，所以我们首先也应该把二维人脸图像使用点坐标来表示。关于人脸关键点检测的算法有很多，这里我们使用 dlib 框架提供的 68 点检测模型，效果图如下

下面我们给出有 68 个关键点的标准3d人脸模型，它看起来就像下面这样

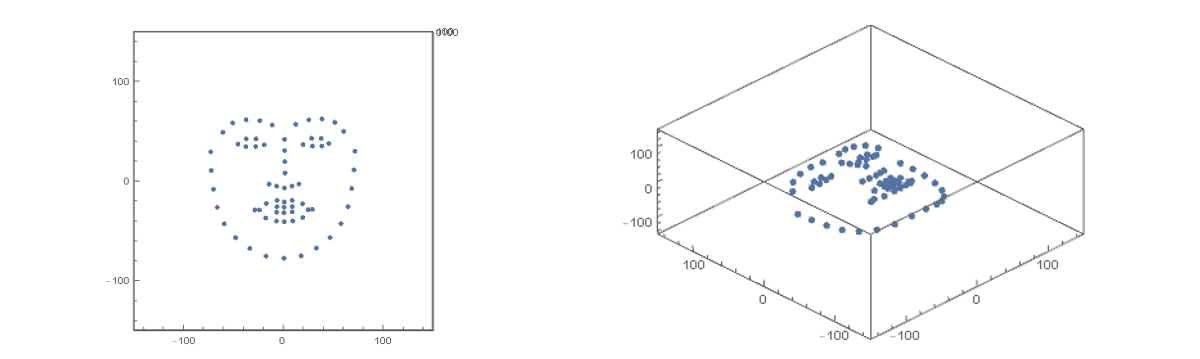
有了标准人脸关键点之后，我们需要对其进行空间变换，也就是前面推导的

\[dst = (src \cdot R + t)\cdot s\]

然后再将其投影到 xy 平面上，当然这个投影矩阵比较简单，只需要提取 dst 中每个点的前两个坐标就可以了

\[prj=\left[ \begin{aligned} &1 \quad 0\\ &0 \quad 1\\ &0 \quad 0 \end{aligned} \right]\]

投影后的点集合为

\[dst_{p} = dst \cdot prj\]

为了衡量投影与图片人脸关键点的重合程度，我们采用平方误差损失函数

\[\begin{aligned} L &= \frac 1 n \sum_{i=1} \mid\mid dst_p(i) - p_i \mid\mid^2\\ &= \frac 1 n \sum_{i=1}^n \mid\mid (src_i \cdot R + t_i)\cdot s \cdot prj - p_i \mid\mid^2 \end{aligned}\]

其中 \(p_i\) 是人脸图像第 i 个关键点的坐标。于是最终要求解的问题便为

\[\alpha,\beta, \gamma = \arg \min_{\alpha, \beta, \gamma} L(\alpha, \beta, \gamma, \lambda_x, \lambda_y, \lambda_z, dx, dy, dz)\]

下面我们采用梯度下降法来求解，参数迭代格式为

\[p = p - \eta \frac{\partial L}{\partial p}\]

其中 \(\eta\) 是学习速率，\(p\) 代表一种参数，也就是前面的 \(\alpha,\beta…\) 等等，经过多次迭代，\(L\) 应该能收敛到一个稳定值，此时便完成了整个优化过程。

接下来，利用上述思路，我们来实际编程试验一下，由于目标函数 \(L\) 的形式还是有点复杂，手动求导不太现实，所以这里我们采用 pytorch 来完成自动求导的功能，首先是定义上面提到的几个参数

alpha = torch.tensor(0.0, requires_grad=True, dtype=torch.float64)
beta = torch.tensor(0.0, requires_grad=True, dtype=torch.float64)
gamma = torch.tensor(0.0, requires_grad=True, dtype=torch.float64)
lambdaX = torch.tensor(1.0, requires_grad=True, dtype=torch.float64)
lambdaY = torch.tensor(1.0, requires_grad=True, dtype=torch.float64)
lambdaZ = torch.tensor(1.0, requires_grad=True, dtype=torch.float64)
dx = torch.tensor(1.0, requires_grad=True, dtype=torch.float64)
dy = torch.tensor(1.0, requires_grad=True, dtype=torch.float64)
dz = torch.tensor(1.0, requires_grad=True, dtype=torch.float64)

由于要对它们求导，所以需要 requires_grad 为 True。然后定义投影到 xy 平面的矩阵

## 投影矩阵
prj = torch.tensor([[1, 0],
                   [0, 1], 
                   [0, 0]], dtype=torch.float64)

以及旋转矩阵

def rx(a): 
    """
     关于x轴的旋转矩阵
    """
    RX = torch.zeros(3, 3, dtype=torch.float64)
    RX[0, 0] = 1
    RX[1, 1] = a.cos()
    RX[1, 2] = -a.sin()
    RX[2, 1] = a.sin()
    RX[2, 2] = a.cos()
    return RX

def ry(b): 
    """
     关于y轴的旋转矩阵
    """
    RY = torch.zeros(3, 3, dtype=torch.float64)
    RY[0, 0] = b.cos()
    RY[0, 2] = b.sin()
    RY[1, 1] = 1
    RY[2, 0] = -b.sin()
    RY[2, 2] = b.cos()
    return RY

def rz(r): 
    """
     关于z轴的旋转矩阵
    """
    RZ = torch.zeros(3, 3, dtype=torch.float64)
    RZ[0, 0] = r.cos()
    RZ[0, 1] = -r.sin()
    RZ[1, 0] = r.sin()
    RZ[1, 1] = r.cos()
    RZ[2, 2] = 1
    return RZ

def r(a, b, r):
    """
    空间旋转矩阵
    """
    R = torch.mm(rx(a), ry(b))
    R = torch.mm(R, rz(r))
    return R

这里我们给旋转矩阵赋值的方式有点怪异，没有直接从数组建立，这是因为旋转矩阵也需要包含梯度信息。

接下来定义空间变换函数和目标函数

def transform(src):
    """
    空间变换
    """
    ## 缩放矩阵
    s=torch.zeros(3, 3, dtype=torch.float64)
    s[0, 0] = lambdaX
    s[1, 1] = lambdaY
    s[2, 2] = lambdaZ
    
    ## 位移向量
    t = torch.zeros(1, 3, dtype=torch.float64)
    t[0, 0] = dx
    t[0, 1] = dy
    t[0, 2] = dz

    R = r(alpha, beta, gamma)
    dst = torch.mm(src, R)+ t
    dst = torch.mm(dst, s)
    return dst

def L(src, p):
    """
    目标函数
    """
    dst = transform(src)
    dst = torch.mm(dst, prj)    
    L = dst - p
    
    return (L[::,0]**2+L[::, 1]**2).sum()/len(src)

最后，以迭代的方式优化目标函数

src = np.loadtxt("/path/to/src.csv")
src = torch.from_numpy(src)

p = np.loadtxt("/path/to/p.csv")
p = torch.from_numpy(p)

iter=128000
lr = 0.00001

def gd(params):
    """
    梯度下降
    """
    for p in params:
        p.data -= lr * p.grad
        p.grad.data.zero_()

for i in range(iter):
    l = L(src, p)
    if i % 1000 ==0:
        print(l)    

    l.backward()
    
    gd([alpha, beta, gamma, lambdaX, lambdaY, lambdaZ, dx, dy, dz])
    

这里我们把学习率设的很小，否则结果不收敛。下面我们用 zack 的脸来跑个例子

首先根据原图来看，zack脸部大致是朝左斜向下的，具体来说，俯仰角（绕 x 轴） \(-\pi/2< pitch <0\)，偏航角（绕y轴）\(-\pi/2< yaw < 0\)，翻滚角（绕z轴）几乎为 0。当然我这里给的范围比较粗糙，主要是为了检验算法是否会得出离谱的结果。

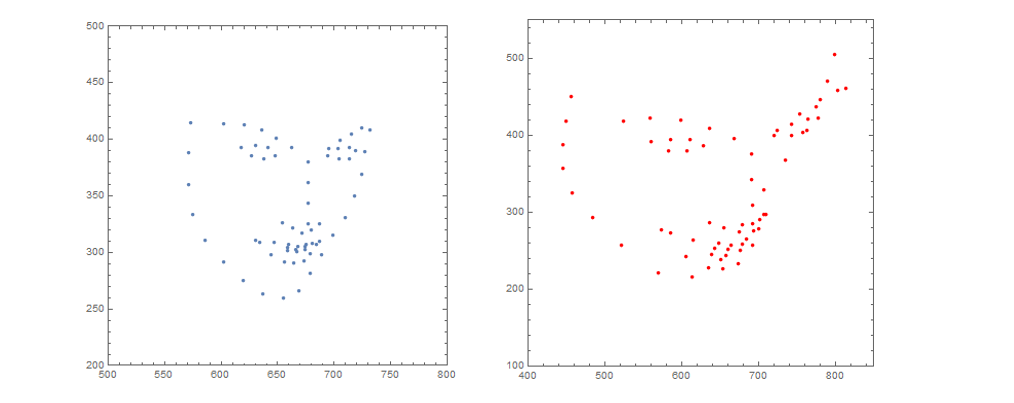
上图左边是原图的人脸关键点，右边是学习出来的结果，两者的面部方向有点差异，但大致上是相同的，可见，我们这个算法有一定效果。当然这只是比较粗糙的实验，用于说明方案的可行性，这里具体的优化算法显得有点暴力，所以时间效率不是很好，后面我们将研究 opencv 所使用的方法。

码字不易，您的支持是我最大的动力，感谢打赏~