为何要对数据归一化或标准化
对数据进行归一化或者标准化是一种常用的数据预处理步骤,一般给出的解释是消除数据量纲差异对模型训练的影响,为了搞清楚会产生何种影响,我们尝试使用自造的数据集来一次模拟分析。
现在给一个3维空间中的平面
\[z(x, y) = 100 x + 20 y\]在此平面附近随机生成样本集合 \(S = {(x_i, y_i, z_i)\mid i=1…n, 0\le x \le 10, 0 \le y \le 50}\),然后利用这个样本集来做回归学习,将模型定义为
\[\hat{z}(x, y) = \theta_1 x + \theta_2 y\]其中 \(\theta_1 , \theta_2\) 便是要训练的系数。
下面我们生成训练数据,方法是在上述平面上取点,并添加随机噪声
random = np.random
# 定义平面方程
z = lambda x, y: 100 * x + 20 * y + random.rand(400)
# 生成随机点
n = 1000
x = random.rand(n) * 10
x = x.astype(int)
y = random.rand(n) * 50
y = y.astype(int)
data=pd.DataFrame([x, y]).T
data.columns=["x", "y"]
data["z"] = data.apply(lambda row: z(row[0], row[1]), axis=1)
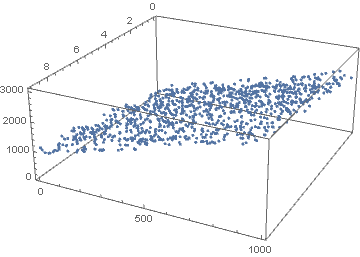
定义平方误差损失函数
\[l(x_i, y_i, z_i) = \left( z_i - \hat{z}(x_i, y_i) \right)^2\]优化目标函数为
\[\begin{aligned} L(\theta_1, \theta_2) &=\frac 1 {2n} \sum_{i=1}^n \left( z_i - \hat{z}(x_i, y_i) \right)^2\\ &=\frac 1 {2n}\sum_{i=1}^n (z_i - \theta_1 x_i - \theta_2 y_i)^2\\ &=\frac 1 {2n}\sum_{i=1}^n (x_i^2\theta_1^2 + y_i^2 \theta_2^2 + 2x_iy_i \theta_1 \theta_2- 2x_iz_i\theta_1 -2y_iz_i \theta_2+ z_i^2) \end{aligned}\]舍去与 \(\theta_1, \theta_2\) 不相关的常数项,我们得到
\[L(\theta_1, \theta_2) = \frac 1 {2n}\left(\sum_{i=1}^n x_i^2 \theta_1^2 + \sum_{i=1}^n y_i^2 \theta_2^2+ 2\sum_{i=1}^n x_i y_i \theta_1 \theta_2 - 2 \sum_{i=1}^nx_i z_i \theta_1 - 2\sum_{i=1}^n y_i z_i \theta_2\right)\]这是一个很简单的凸优化问题,具有全局最优解,利用刚才生成的样本集,我们画出目标函数的图像可以更直观的看到这一点
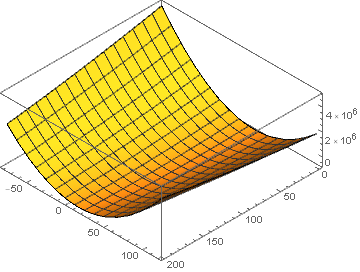
在应用梯度下降法求解问题时
\[(\theta_1, \theta_2) = \arg \min_{\theta_1, \theta_2} L(\theta_1, \theta_2)\]其迭代格式为
\[\theta^{(n+1)} = \theta^{(n)} - \alpha \frac{\partial L}{\partial \theta}\mid_{\theta = \theta^{(n)}}\]上式的几何意义是,参数点 \((\theta_1, \theta_2)\) 沿着目标函数梯度方向以步长为 \(\alpha\) 前进。下图,我们在目标函数的等高线图上标出了训练过程
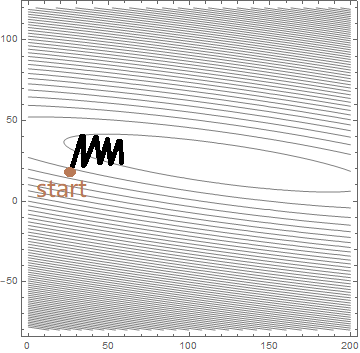
可以看到,从初始点开始,每一次迭代,参数的更新方向都垂直于等高线,逐步接近椭圆中心(也就是最优点)。但同时也发现,参数更新的路径十分怪异,它以Z字形的方式来回震荡,导致收敛速度十分缓慢。很明显,造成这种震荡的直接原因就在于这椭圆形的等高线,更深层次的原因则是目标函数中 \(\theta_1, \theta_2\) 的系数量级的不同。在这个例子中
\[\sum_{i=1}^n x_i^2 = 27995, \quad\sum_{i=1}^n y_i^2 = 787213\]接下来我们对训练集做归一化处理
from sklearn.preprocessing import MinMaxScaler
minmax = MinMaxScaler()
minmax.fit(data)
normalize_data=minmax.transform(data)
依照前面的方法计算出目标函数,其等高线如下所示
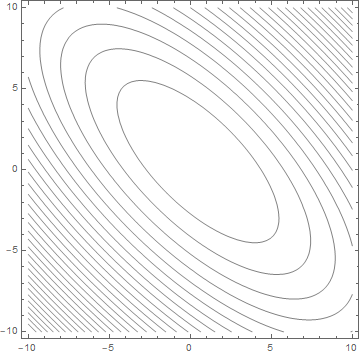
这时椭圆的长轴于短轴之比已明显小于未归一化的数据,也就是说,前面提到的震荡效应可以很大程度上被减弱。可见,数据归一化能够有效提高模型训练的收敛速度。