如何使用算法抠图——Closed Form Matting 算法以及优化-1
本文算法思想主要来自于下文,算法优化部分为原创
A. Levin, D. Lischinski and Y. Weiss, “A Closed-Form Solution to Natural Image Matting,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 30, no. 2, pp. 228-242, Feb. 2008.
我们先对算法进行介绍,然后再考虑优化问题。
简介
抠图是一种很常见的图像处理应用,简单来说,抠图就是保留需要的像素,并删去图片的其他部分。于是潜在地,图片就被分为了两个部分,被称为前景和背景,若前景像素用 F 表示,背景像素用 B 来表示,那么图片中的每个像素都能通过是 F 和 B 的线性插值得到
\[I = \alpha F + (1 - \alpha) B\]其中向量 \(\alpha\) 的每个元素是对应像素的透明度。对于一张待抠取的图片来说,\(I\) 是已知的,因为这是能看见的部分,而 \(F, B, \alpha\) 属于未知量,因为不同的抠图目的,前景和背景的定义肯定不同。进一步,对于一般有三个颜色通道的 RGB 图片,那么在每个通道上都能列出一个方程,于是有
\[\begin{aligned} I_r = \alpha F_r + (1 - \alpha) B_r\\ I_g = \alpha F_g + (1 - \alpha) B_g\\ I_b = \alpha F_b + (1 - \alpha) B_b \end{aligned}\]也就是说,在每个像素上,都能得到一个像上面这样的线性方程组,但却有 7 个未知量,因此需要添加额外的约束条件。如果能解出上述方程组,那么只需单独拿出前景部分,问题就解决了。
目标函数推导
为了简化讨论,首先从单通道问题入手,即求解方程组
\[I_i = \alpha_i F_i + (1 - \alpha_i) B_i\]这里的下标 \(i\) 表示像素索引。假设在图片的任意一个像素窗口 \(w_j\) 上(如图所示)(其中 j 表示窗口索引),\(F_i, B_i ,\alpha_i\) 近似为常量,那么上述等式关系可以在该窗口上近似成立,即
\[I_i \approx \alpha_i F_j + (1 - \alpha_i) B_j \,,\quad i \in w_j\]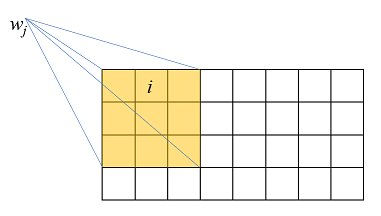
对上述方程进行变换
\[\begin{aligned} I_i &\approx \alpha_i F_j + (1 - \alpha_i) B_j\\ \Rightarrow I_i &\approx\alpha_i F_j + B_j - \alpha_i B_j\\ \Rightarrow \alpha_i &\approx \frac {I_i} {F_j - B_j} - \frac{B_j}{F_j - B_j}\\ \Rightarrow \alpha_i &\approx a_j I_i + b_j \,,\quad i \in w_j \end{aligned}\]其中 \(a = \frac 1 {F_j - B_j}, b = - \frac{B_j}{F_j - B_j}\),也就是说,如果在窗口 \(w_j\) 上,能找到 \(\alpha_i, a_j, b_j\) 使上述公式成立,那么问题就解决了。如果令
\[J_j(\alpha_i,a_j, b_j) = \sum_{i \in \omega_j} (\alpha_i - a_j I_i - b_j)^2 \,,\quad i \in w_j\]那么问题便转换成了求解 \(J_j(\alpha_i, a_j, b_j)\) 取最小值时的参数,由于整张图是由许多互相重叠的窗口组成的,那么总体的目标函数就可以表达为
\[J(\alpha, a, b) = \sum_{j \in W}\left(\sum_{i \in \omega_j} (\alpha_i - a_j I_i - b_j)^2 + \epsilon a_j^2\right)\]其中 \(W\) 表示窗口索引集合,\(\epsilon\) 表示正则项系数。若假设窗口尺寸为 3 x 3 ,且窗口总数为 n,那么
\[\begin{aligned} J(\alpha, a, b) &= \sum_{k=1}^n\left(\sum_{i =1}^9 (\alpha_{ki} - a_k I_{ki} - b_j)^2 + \epsilon a_j^2\right)\\ &= \sum_{k=1}^n \left( \left| \left[ \begin{aligned} a_k I_{k1} + b_k \\...\\ a_k I_{k9} + b_k\\\sqrt{\epsilon}a_k \end{aligned} \right] - \left[ \begin{aligned} \alpha_{k1}\\...\\\alpha_{k9} \\0 \end{aligned} \right] \right|^2 \right) \\ &= \sum_{k=1}^n \left( \left| \left[ \begin{aligned} I_{k1} &\quad 1 \\...\\ I_{k9} &\quad 1\\\sqrt{\epsilon}&\quad 0 \end{aligned} \right] \cdot \left[\begin{aligned} a_k \\ b_k \end{aligned}\right] - \left[ \begin{aligned} \alpha_{k1}\\...\\\alpha_{k9} \\0 \end{aligned} \right] \right|^2 \right) \end{aligned}\]若令
\[G_k = \left[ \begin{aligned} I_{k1} &\quad 1 \\...\\ I_{k9} &\quad 1\\\sqrt{\epsilon}&\quad 0 \end{aligned} \right] , \bar{\alpha}_k = \left[ \begin{aligned} \alpha_{k1}\\...\\\alpha_{k9} \\0 \end{aligned} \right] , c_k = \left[\begin{aligned} a_k \\ b_k \end{aligned}\right]\]则目标函数可以写成矩阵形式
\[J(\alpha, a, b) = \sum_{k = 1}^n \left|G_k \cdot c_k -\bar{\alpha}_k \right|^2\]为了最小化目标函数,在每一个窗口上对其求偏导数,并令偏导数等于 0
\[\frac{\partial J(\alpha, a, b)}{\partial c_k} = 2G_k^T (G_k c_k - \bar{\alpha}_k) = 0\]通过上式,计算 \(c_k\) 等于
\[c_k = (G_k^T G_k)^{-1}(G_k \bar{\alpha}_k)\]将上式代入目标函数后,得到只与 \(\alpha\) 有关的目标函数
\[\min J(\alpha, a,b) = \min_{c_k = (G_k^T G_k)^{-1}(G_k \bar{\alpha}_k)} J(\alpha)\]其中
\[\begin{aligned} G_k \cdot c_k - \bar{\alpha}_k&= G_k (G_k^T G_k)^{-1} G_k^T \bar {\alpha}_k - \bar{\alpha}_k \\ &= \left[G_k (G_k^T G_k)^{-1} G_k^T - I\right] \bar{\alpha}_k\\ &= \bar{G}_k \bar{\alpha}_k \end{aligned}\]在这里 \(\bar{G}_k=G_k (G_k^T G_k)^{-1} G_k^T - I\),于是
\[\begin{aligned} J(\alpha) &=\sum_{k=1}^n \left|G_k \cdot c_k -\bar{\alpha}_k \right|^2\\ &= \sum_{k=1}^n (G_k \cdot c_k -\bar{\alpha}_k)^T (G_k \cdot c_k -\bar{\alpha}_k)\\ &=\sum_{k=1}^n \bar{\alpha}_k^T \bar{G}_k^T \bar{G}_k \bar{\alpha}_k \\ &= \sum_{i=1}^n \bar{\alpha}_k^T L_k \bar{\alpha}_k \end{aligned}\]在上面最后一步中 \(L_k = \bar{G}_k^T \bar{G}_k\)。当然这只是在单通道图片(即灰度图)中的情况,接下来讨论彩色图片的情况。
彩色图片情况
在彩色图片中,以 RGB 模式为例,每个像素点都有 3 个颜色值,这就组成了一个颜色空间,以下图为例
![]()
如果用每个像素点的 RGB 值为坐标,则该图片在颜色空间中的形状如下
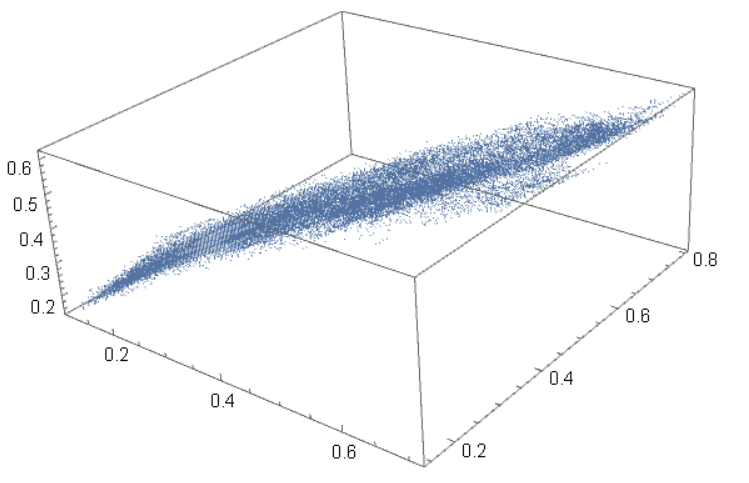
可以看到,这些点大致呈线性关系,为了进一步说明,我们随机选择 9 个 3 x 3 的像素窗口,并绘制像素点在颜色空间中的位置,如下所示
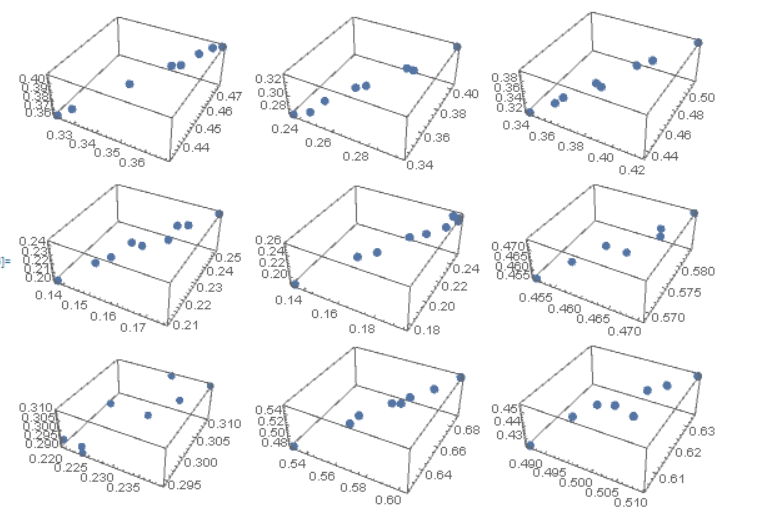
同样也呈现出明确的线性关系,于是给出如下假设:
在彩色图片上的一个小范围内,所有像素点在颜色空间中大致呈线性排列,即 \(I_i = \beta_i I_1 + (1 - \beta_i) I_2\)
当然,前景和背景颜色同样满足上述关系,于是在任一个像素窗口 \(w_j\)内有
\[\begin{aligned} F_i &= \beta_i^F F_1 + (1- \beta_i^F)F_2\\ B_i &= \beta_i^B B_1 + (1- \beta_i^B)B_2 \end{aligned}\]其中的 \(F_1, F_2, B_1, B_2\) 是与具体窗口有关的量,它们描述了此窗口的像素点在颜色空间中的方向,然后代入公式
\[I_i = \alpha_i F_i + (1 - \alpha_i) B_i\]得到
\[\begin{aligned} & I_i = \alpha_i \beta_i^F F_1 + \alpha_i (1 - \beta_i^F) F_2 + (1-\alpha_i) \beta_i^B B_1 + (1-\alpha_i)(1 - \beta_i^B) B_2\\ & \Rightarrow I_i - B_2 = \alpha_i \beta_i^F F_1 - \alpha_i \beta_i^F F_2 + \alpha_i F_2 + \beta_i^B B_1 - \alpha_i \beta_i^B B_1 + \alpha_i \beta_i^B B_2 -\beta_i^B B_2 - \alpha_i B_2 \\ &\Rightarrow I_i - B_2 = \alpha_i \beta_i^F (F_1 - F_2) +( \beta_i^B - \alpha_i \beta_i^B) (B_1 - B_2) + \alpha_i (F_2- B_2 )\\ &\Rightarrow \left[(F_1 - F_2)\quad (B_1 - B_2) \quad (F_2 - B_2)\right]\cdot \left[\begin{aligned} \alpha_i \beta_i^F \\ \beta_i^B - \alpha_i \beta_i^B\\ \alpha_i \end{aligned}\right] = I_i - B_2 \end{aligned}\]由于在多通道情况中,每个像素都有 3 个颜色值,所以这里的\(F_i, B_i, I_i\) 都是 3 x 1 的向量,所以上式又可展开成
\[\left[ \begin{aligned} (F_1^1 - F_2^1)\quad (B_1^1 - B_2^1) \quad (F_2^1 - B_2^1)\\ (F_1^2 - F_2^2)\quad (B_1^2 - B_2^2) \quad (F_2^2 - B_2^2)\\ (F_1^3 - F_2^3)\quad (B_1^3 - B_2^3) \quad (F_2^3 - B_2^3) \end{aligned} \right] \cdot \left[\begin{aligned} \alpha_i \beta_i^F \\ \beta_i^B - \alpha_i \beta_i^B\\ \alpha_i \end{aligned}\right] = \left[ \begin{aligned} I_i^1 - B_2^1\\I_i^2 - B_2^2\\I_i^3 - B_2^3 \end{aligned} \right]\]若令
\[H_j = \left[(F_1 - F_2)\quad (B_1 - B_2) \quad (F_2 - B_2)\right]\]则有
\[\left[\begin{aligned} \alpha_i \beta_i^F \\ \beta_i^B - \alpha_i \beta_i^B\\ \alpha_i \end{aligned}\right] = H_j^{-1} \cdot \left[ \begin{aligned} I_i^1 - B_2^1\\I_i^2 - B_2^2\\I_i^3 - B_2^3 \end{aligned} \right]\]假设 \(H_j^{-1}\) 的最后一行等于 \([a_j^1\quad a_j^2 \quad a_j^3]\),那么可以得到
\[\begin{aligned} \alpha_i &= a_j^1 (I_i^1 - B_2^1) + a_j^2 (I_i^2 - B_2^2) + a_j^3 (I_i^3 - B_2^3)\\ &= \sum_{t=1}^3 a_j^t I_i^t + b_j \end{aligned}\]接下来,与之前单通道情况类似,定义目标函数
\[J(\alpha, a, b) = \sum_{j\in W} \left( \sum_{i \in w_j} \left( \alpha_i - \sum_{t=1}^3 a_j^t I_i^t - b_j \right)^2 + \epsilon \sum_{t=1}^3(a_j^t)^2 \right)\]用和之前一样的方法,将上式化简为
\[J(\alpha, a, b) = \sum_{i = 1}^n \left| G_k c_k -\bar{\alpha}_k \right|^2\]其中
\[G_k = \left[ \begin{aligned} I_1^1 \quad I_1^2 \quad I_1^3 \quad 1 \\ I_2^1 \quad I_2^2 \quad I_2^3 \quad 1 \\ I_3^1 \quad I_3^2 \quad I_3^3 \quad 1 \\ ...\\ I_9^1 \quad I_9^2 \quad I_9^3 \quad 1 \\ \sqrt{\epsilon} \quad 0 \quad 0 \quad 0 \\ 0 \quad \sqrt{\epsilon} \quad 0 \quad 0 \\ 0 \quad 0 \quad \sqrt{\epsilon} \quad 0 \end{aligned} \right], c_k = \left[ \begin{aligned} a_j^1 \\ a_j^2 \\ a_j^3 \\ b_j \end{aligned} \right] ,\bar\alpha_k = \left[ \begin{aligned} \alpha_{k_1}\\ \alpha_{k_2}\\ \alpha_{k_3}\\ ... \\ \alpha_{k_9}\\ 0 \\ 0 \\ 0 \end{aligned} \right]\]之后同样可推得
\[J(\alpha) = \sum_{i=1}^n \bar{\alpha}_k^T L_k \bar{\alpha}_k\]构建拉普拉斯矩阵
首先,我们复习下矩阵乘法的分块形式,假设矩阵 \(M\) 和向量 \(v\) 按如下分块
\[M =\left[ \begin{aligned} M_{00} &\quad M_{01} \\ M_{10} &\quad M_{11} \end{aligned} \right], v = \left[ \begin{aligned} v_1 \\ v_2 \end{aligned} \right]\]那么
\[\begin{aligned} v^TMv &= [v_0^T \quad v_1^T] \left[ \begin{aligned} M_{00} &\quad M_{01} \\ M_{10} &\quad M_{11} \end{aligned} \right] \left[ \begin{aligned} v_0 \\ v_1 \end{aligned} \right] \\ &=[v_0^T M_{00} + v_1^T M_{10} \quad v_1^T M_{01} + v_1^T M_{11}] \left[ \begin{aligned} v_0 \\ v_1 \end{aligned} \right]\\&=v_0^T M_{00}v_0 + v_0^T M_{10}v_1 + v_1^T M_{01} v_0 + v_1^T M_{11} v_1 \end{aligned}\]如果我们假设 \(M_{10} = 0, M_{01} = 0\),即 \(M\) 是一个带状矩阵,那么就有
\[v^T M v = \sum_{i=0}^1 v_i^T M_{ii} v_i\]这让我们看到了和前面推导的公式的相似之处
\[J(\alpha) = \sum_{i=1}^n \bar{\alpha}_k^T L_k \bar{\alpha}_k\]而且我们知道,\(\bar{\alpha}_k\) 其实就是向量 \(\alpha\) 的一个子向量,这和 \(v_i\) 与 \(v\) 的关系相当,唯一的区别是 \(\bar{\alpha}_k\) 元素的位置在 \(\alpha\) 上不是连续的,但这并不重要。于是,通过这种类比,我们可以推断,存在一个矩阵 \(L\) ,使得
\[J(\alpha) = \sum_{i=1}^n \bar{\alpha}_k^T L_k \bar{\alpha}_k = \alpha^T L \alpha\]由于刚才我们假设 \(M\) 是带状矩阵,那么有理由相信 \(L\) 肯定也是带状矩阵。因为 \(\bar{\alpha}_k\) 在 \(\alpha\) 上不是连续的,对于单个 \(\bar{\alpha}_k^T L_k \bar{\alpha}_k\) 来说,其乘法关系在全量的矩阵表示形式下如图所示,图中黑色的部分代表对应的 \(\bar{\alpha}_k\) 和 \(L_k\)。
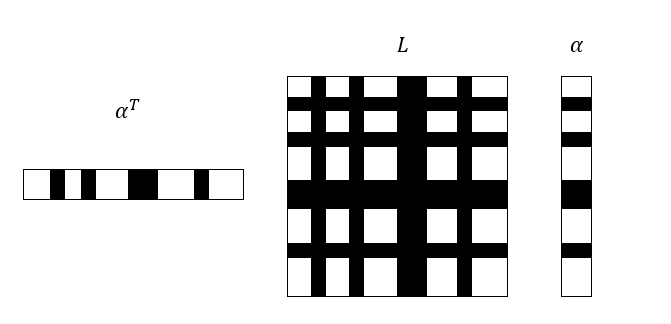
现在,我们面临着和矩阵乘法分块相反的问题,那就是把已经分块的矩阵重新拼凑成原矩阵,即组装 \(L\)。这与有限元中通过单元刚度矩阵组装总体刚度矩阵的方法十分相似,说不定它们之间还存在着更深刻的联系。
在讨论如何通过 \(L_k\) 来组装 \(L\) 之前,我们先回顾 \(\bar{\alpha}_k, \alpha\) 这两个量的物理意义,\(\alpha\) 是由每个像素的透明度组成的向量,由于图片是二维的,所以我们按横向扫描所有像素,它的具体形式为
\[\alpha = [\alpha_1 \quad \alpha_2 \quad ... \quad \alpha_N]^T\]而 \(\bar{\alpha}_k\) 是第 \(k\) 个窗口的所有像素透明度组成的向量,同样按横向扫描
\[\bar{\alpha}_k = [\alpha_{k_1} \quad \alpha_{k_2}\quad ...\quad \alpha_{k_9}]^T\]其中的下标 \(k_1, k_2,…\) 等是 \(\alpha\) 中的元素索引。这里需要注意一下,前面在定义 \(\bar{\alpha}_k\) 的时候,最后还有一个元素为 0,这里我们去掉了,因为可以证明,如果向量 \(v\) 的某些位等于 0,那么只需要去掉这些位,以及相应的 \(M\) 的行和列,其结果是等价的
\[v^T M v = \hat{v}^T \hat{M}^T \hat{v}\]其中 \(\hat{v},\hat{M}\) 是修改之后的向量和矩阵。
现在我们举个简单的例子,假设
\[\alpha = [\alpha_1 \quad \alpha_2 \quad \alpha_3 \quad \alpha_4]^T\] \[\bar{\alpha}_k = [\alpha_1 \quad \alpha_2\quad \alpha_4]^T\] \[L_k = \left[ \begin{aligned} L_{11}^k&\quad L_{12}^k \quad L_{13}^k\\ L_{21}^k&\quad L_{22}^k \quad L_{23}^k\\ L_{31}^k&\quad L_{32}^k \quad L_{33}^k \end{aligned} \right]\]那么按照向量矩阵乘法的要求, \(L_k\) 在 \(L\) 中的位置分布如下
\[L = \left[ \begin{aligned} L_{11}^k&\quad L_{12}^k\quad 0 \quad L_{13}^k\\ L_{21}^k&\quad L_{22}^k\quad 0 \quad L_{23}^k\\ 0&\quad 0\quad \quad0 \quad 0\\ L_{31}^k&\quad L_{32}^k\quad 0 \quad L_{33}^k \end{aligned} \right]\]也就是说,\(L_k\) 的元素在 \(L\) 中的位置与 \(\bar{\alpha}_k\) 元素的下标有关,其对应关系为
\[L_k(i, j) \rightarrow L(k_i, k_j)\]其中 \(k_i\) 为 \(\bar{\alpha}_k\) 中第 \(i\) 个元素的下标。由于不同的 \(L_k\) 可能在 \(L\) 上的位置重叠,我们只需要将它们相加即可,因为矩阵乘法只是简单的线性操作。
使用上述方法构造出 \(L\) 之后,我们便得到了关于目标函数的新的表示形式
\[J(\alpha)=\sum_{i=1}^n \bar{\alpha}_k^T L_k \bar{\alpha}_k = \alpha^T L \alpha\]其中,\(L\) 又被称为拉普拉斯矩阵。从而,优化的目标为
\[\min_{\alpha}\quad \alpha^T L \alpha\]根据前面我们对 \(\bar{G}_k, L_k, L\) 的推导可以证明, \(L\) 的每一个元素都是非负的,并且按照定义 \(\alpha\) 的每一个元素也是非负的,这样一来,就只需要令 \(\alpha\) 的每一个元素都为 0,从而使 \(\alpha^T L \alpha\) 达到极小值 0,但这显然毫无意义。
这里的问题就出在我们没有对 \(\alpha\) 施加约束条件,因为,我们知道肯定有一部分 \(\alpha_i\) 是等于 1 的(即我们要提取的前景),所以大部分抠图算法都要求使用者提供约束条件,也就是说,给出部分绝对正确的前景和背景。Trimap 图便是一种这样的约束形式。


考虑上面第一张图,如果我们要抠取小狗的图像,那么其对应的 trimap 图如第二张图所示。其实就是把原图分割成三个部分,分别是100%背景,100%前景以及不那么确定的部分,这个不确定的部分就是我们要求解的,其余的都算约束。于是加上约束的优化目标就变成了
\[\begin{aligned} &\min \alpha^T L \alpha\\ s.t. \quad &\alpha_i = 0 \quad for \quad i\in BG\\ &\alpha_i = 1 \quad for \quad i\in FG \end{aligned}\]其中 \(BG\) 是背景索引集合,\(FG\) 是前景索引集合。
问题的求解
现在我们使用拉格朗日乘子法来求解该问题,首先建立拉格朗日函数
\[\begin{aligned} l(\alpha, \lambda) &= \alpha^T L \alpha + \sum_{i\in BG}\xi_i \alpha_i + \sum_{i\in FG} \eta_i (1-\alpha_i) \\ &=\alpha^T L \alpha + \sum_{i=1}^N \lambda_i \alpha_i + \sum_{i\in FG}\eta_i\\ &=\alpha^T L \alpha + \lambda \alpha + C \end{aligned}\]其中 \(C\) 为常数,\(\lambda\) 在索引 \(i \notin BG \land i\notin FG\) (即 \(\alpha_i\) 未知)上的值为 0。然后计算拉格朗日函数对 \(\alpha\) 的导数,并令其等于 0,便可获得最优解
\[\frac{\partial l(\alpha, \lambda)}{\partial \alpha} = L \alpha + \lambda = 0\]于是,问题转化成了求解线性方程组
\[L\alpha = -\lambda\]需要注意的是,\(\alpha\) 和 \(\lambda\) 中都有部分是已知量,并且在\(\alpha\) 上是未知量的索引,在 \(\lambda\) 上的值刚好等于 0。我们可以用下图直观的表示
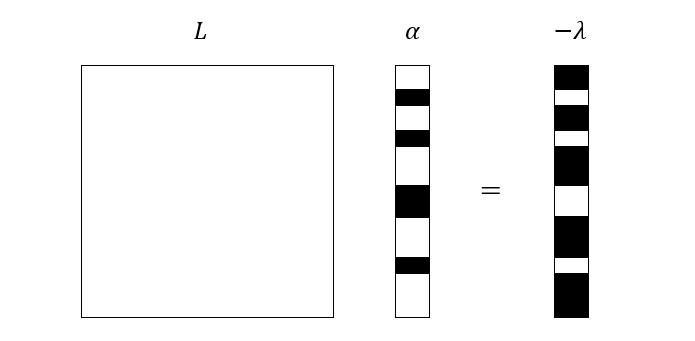
其中黑色部分都是未知量。关于这种情况的线性方程组,有好几种方法可以求解,其中一类方法选择将 \(\lambda\) 未知的部分填充,以其中一个方程为例
\[L_{11}\alpha_1 + L_{12} \alpha_2 + ... + L_{1N} \alpha_N = -\lambda_1\]假如这里的 \(\alpha_1\) 已知,\(\lambda_1\) 未知,如果在 \(L_{11}\) 前面乘以一个非常大的数,比如\(10e20\),并令 \(-\lambda_1=10e20 L_{11}\),即方程变为
\[10e20 L_{11}\alpha_1 + L_{12} \alpha_2 + ... + L_{1N} \alpha_N =10e20 L_{11}\]很显然,后续 \(L_{12} \alpha_2, L_{13}\alpha_3… \) 之和与 \(10e20\) 相比都是极小的量,于是求解出来的 \(\alpha_1\) 和其本身的值也会相差无几。使用这种方式修改每一个未知的 \(\lambda_i\) 和对应的 \(L_{ii}\),得到可以正常求解的线性方程组,按一般方式进行求解即可。
存储与求解形式的优化
以一张 1080p 的图片为例,两个方向上的像素分别有 1920 和 1080 个,总的像素数量为 2073600 个,那么矩阵 \(L\) 的维度也就为 2073600,于是总的元素数量就等于 \(2073600^2\)。这是一个相当大的矩阵,使得这种算法几乎不可应用。幸运的是,\(L\) 本身的性质能节省大量的存储空间,根据 \(L_k\) 的定义
\[L_k = \bar{G}_k^T \bar{G}_k\]可见,\(L_k\) 是对称矩阵,从而 \(L\) 也是对称的。而且,\(L\) 本身是一个带状矩阵,那么其带宽是多大呢?我们可以从 \(L\) 的组装方式来分析
\[L_k(i, j) \rightarrow L(k_i, k_j)\]对于 \(L\) 的第 \(r\) 行来说,只要第\(k\) 个窗口的 \(k_i = r\),那么此时 \(L_k(i, j)\) 便被填充到 \(L\) 矩阵的 \(r\) 行中,列号为 \(k_j\)。而这里的 \(r\) 只是图片的一个像素索引,包含此索引的窗口如下图所示(我们已用不同颜色的虚线标出)
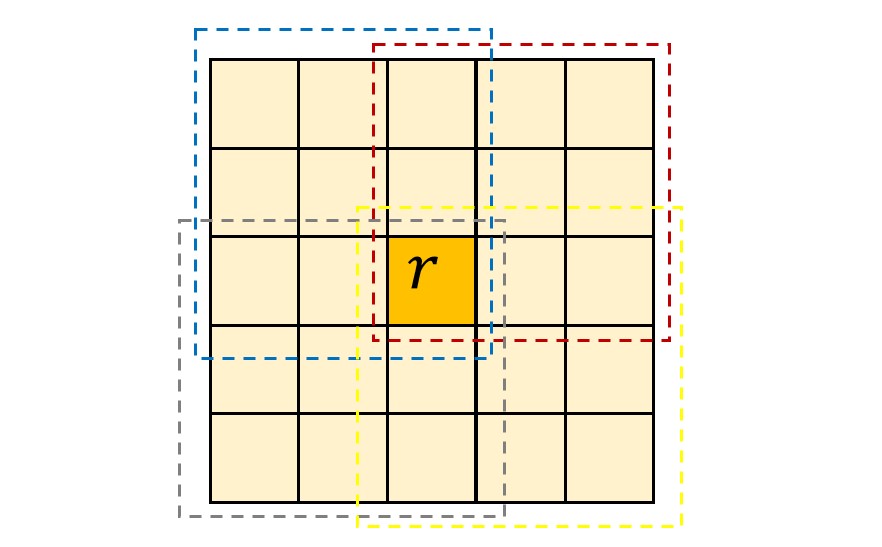
若设图片的宽度为 \(w\) 像素,那么我们可以利用 \(r\) 推断上图中所有像素点的索引,即从小到大为
\[r - 2 - 2 w, r-1-2w,r-2w,...,r+2w, r+1 +2w ,r+2+2w\]由于\(k_j\) 要取遍上述所有值,并且要被填充到第 \(r\) 行,那么填充的中心就为第 \(r\) 列,填充的宽度为 \(r+2+2w - (r - 2 - 2 w) = 4 w\)
既然第 \(r\)行的填充中心为第\(r\)列,且填充宽度为 \(4w\),于是整个矩阵 \(L\) 的带宽也就为 \(4w\)。再考虑到 \(L\) 是对称矩阵,那么真正需要存储的元素个数就变成了
\[(h \times w) \times 2 w\]其中 \(h\) 为图片的高度。对比全矩阵的 \((h\times w)^2\),存储量已大幅减少。但这还远为结束,如果再仔细观察上面图中窗口像素的索引
\[\begin{aligned} r-2-2w,r-1-2w, r-2w, r+1-2w, r+2-2w\\ r-2-w,r-1-w, r-w, r+1-w, r+2-w\\ r-2,r-1, r, r+1, r+2\\ r-2+w,r-1+w, r+w, r+1+w, r+2+w\\ r-2+2w,r-1+2w, r+2w, r+1+2w, r+2+2w\\ \end{aligned}\]可以看到,每行的填充区域被分成了五个区域,这些区域之间的部分的值其实也是 0。所以每一行,真正被填充的只有 25 列,这样一来,总共需要被存储的元素就降为了 \(25 w \times h / 2\)。
这还没完,虽然我们刚才对需要存储的矩阵元素数量进行了大幅优化,但是需要求解的线性方程组规模仍然很宏大。我们已经知道 \(\alpha\) 中有部分值是已知的,那么是否可以把这部分的计算量给省出来呢?答案是显然的。前面,我们为了获得完整的线性方程组,将 \(\lambda\) 的未知部分给填充了,但下面的事实将表明,这一行动似乎是多此一举。现在,我们将 \(\alpha\) 元素的顺序调整一下,分成已知的和未知的两个部分,并且 \(L, \lambda\) 也进行相应调整,得到
\[\begin{aligned} &\left[ \begin{aligned} L_{11}\quad L_{12}\\ L_{21}\quad L_{22} \end{aligned} \right] \left[ \begin{aligned} \alpha_{unknown}\\ \alpha_{known} \end{aligned} \right]= \left[ \begin{aligned} \lambda_{known}\\ \lambda_{unknown} \end{aligned} \right]\\ \Rightarrow& L_{11} \alpha_{unknown} + L_{12} \alpha_{known} = \lambda_{known}\\ \Rightarrow & L_{11}\alpha_{unknown} = -L_{12}\alpha_{known} + \lambda_{known} \end{aligned}\]可以看到,这里我们直接忽略掉 \(\lambda\) 未知的那部分,从而得到了一个与原先等价的,但却更小的线性方程组。该方程组的个数等于未知 \(\alpha\) 元素的数量,即 trimap 图中灰色的部分,可见,此时问题的规模急剧减小,并且跟图片本身的大小解耦,这样一来通过控制 trimap 未知区域的大小就可以控制问题的规模,比如说,未知区域的面积占图片面积的 1/10,那么需要求解的线性方程组则是原来的 1/100。
从理论上分析了优化方案之后,接下来我们该讨论具体的算法和数据结构了。但在这之前,我们来捋一捋从方程构建到求解的整个过程
- 首先,需要两张图,一张是需要抠取内容的原图,另一张是表示约束的 trimap 图。
- 使用小窗口对原图进行扫描,移动步长为一个像素,即这些窗口是相互重叠的,并在每个窗口上构建矩阵 \(L_k\)
- 通过大量的小矩阵 \(L_k\) 组装拉普拉斯矩阵 \(L\)(这一步有待优化)
- 利用 trimap 图构造 \(\alpha\) 和 \(\lambda\)
- 求解线性方程组 \(L\alpha = \lambda\)(待优化)
虽然我们顺序地给出了上述过程,但是这并不意味着必须严格按照顺序执行,比如可以在构建 \(L_k\) 的同时将其累加到 \(L\) 矩阵,于是便省去了存储 \(L_k\) 的空间。并且也不必构造全量的 \(L\),而是只需要得到与 \(\alpha_{unknown}\) 相关的的行和列,即前面的 \(L_{11}\),并可以按稀疏格式存储。这样一来每个 \(L_k\) 的元素就会经历两次位置映射,第一次是从 \(L_k\) 中的位置,映射到 \(L\) ,第二次从 \(L\) 映射到 \(L_{11}\)。具体实现我们留到下一篇文章中讨论。