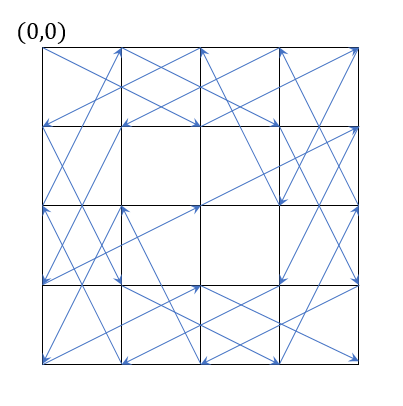
算法题:棋盘行走
在象棋规则里面,马总是按日字对角移动,现在假设有一个横向 m 条线,纵向 n 条线的棋盘,马 位于交点 (x,y) 上。如果要让马走完棋盘上的每一个点,请问有多少条路线?
这里我们先理一下思路,在棋盘上的每一个点,棋子都有 0 种,1种或者多种移动方法,如果把当前所在的点,作为一个节点,那么下一步选择要走的点其实就是在选择子节点
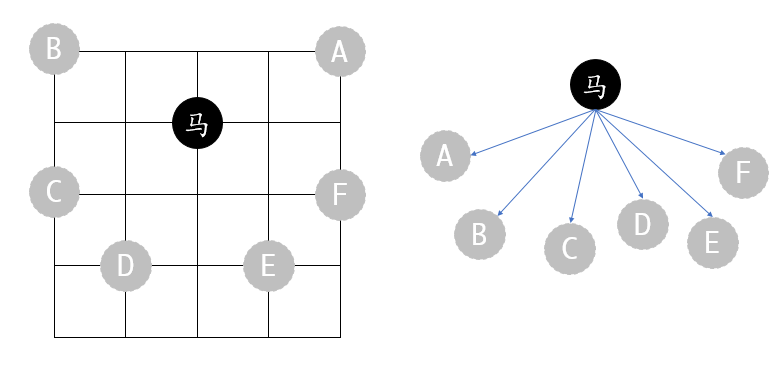
比如上图的马,就有6种走法,等价于有6个子节点,所有可能的移动路径用节点连接起来就成了一个图结构。棋子的每一条移动路径,都可以用图中的一条路径来表示,于是我们的问题就变成了搜索图的每一条路径,如果该路径上的节点与棋盘上的点一一对应,那么这就是一条符合条件的路线。
现在我们来考虑一下数据结构的问题。首先把棋盘上所有的点表示出来,每个点都可以用一个节点对象来表示,它有一些属性,包括坐标、相邻节点数组以及是否被访问标记
public class Node{
public final int x;
public final int y;
private List<Node> neighbors = new ArrayList<>();
private boolean hasVisited = false;
public Node(int x, int y){
this.x = x;
this.y = y;
}
public void addNeighbor(Node node){
neighbors.add(node);
}
public List<Node> getNeighbors(){
return neighbors;
}
public boolean hasVisited(){
return hasVisited;
}
public void visit(){
hasVisited = true;
}
public void reset(){
hasVisited = false;
}
public String toString(){
return "(" +x+","+y+ ")";
}
}
注意这里的相邻节点,指的是马能够一步抵达的节点。接下来建立节点数组
List<Node> nodes = new ArrayList<>();
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
nodes.add(new Node(i, j));
}
}
上面的代码只定义了基本的节点坐标,还需要为每个节点添加相邻节点数组,原理很简单,对于坐标为 (x, y) 的点,它的潜在相邻节点为
\[(x-2,y-1)\,,(x-2,y+1)\\(x-1,y-2)\,,(x-1,y+2)\\(x+1,y-2)\,,(x+1,y+2)\\(x+2,y-1)\,,(x+2,y+1)\]当然上面这些点可能并不完全合法,如果 (x, y) 靠近边界,那么有些坐标可能就超出棋盘范围了。找到合法的相邻节点之后,再加入 neighbor 数组就完成了邻接链表的创建。
for (Node node : nodes) {
List<Node> nbs = calcNeighborsOf(node);
for (Node nb : nbs) {
node.addNeighbor(nb);
}
}
现在我们就可以应用深度优先搜索了,从初始节点 (x, y) 开始递归向下,每经过一个节点,就将该节点的 hasVisited 设为 true ,并且加入到访问节点数组。在选择子节点的时候,可以从 neighbor 数组的第一个节点开始,但是需要注意如果子节点已经被访问过了,就跳过该子节点,如果发现所有子节点都被访问过了,那么就检查访问节点数组是否包含所有节点,如果是,就说明我们找到了一条路线覆盖了所有点。然后将该节点的 hasVisited 设为 false ,并将其移除访问节点数组,因为这条路线已经排查完了,不能影响其他路线。搜索代码如下
public void dfs(Node start){
List<Node> visited = new ArrayList<>();
dfs(start, visited);
}
private void dfs(Node current, List<Node> visited){
current.visit();
visited.add(current);
boolean end = true;
for (Node node : current.getNeighbors()) {
if(!node.hasVisited()) {
end = false;
dfs(node, visited);
}
}
if(end) {
if(visited.size() == m * n) {
System.out.println(visited);
}
}
current.reset();
visited.remove(visited.size() - 1);
}
当 n = m = 5 时,其中一条可行路径如下
[(0,0), (1,2), (0,4), (2,3), (0,2), (1,0), (3,1), (4,3), (2,4), (0,3), (1,1), (3,0), (2,2), (1,4), (3,3), (4,1), (2,0), (0,1), (1,3), (3,4), (4,2), (2,1), (4,0), (3,2), (4,4)]