算法题:背包问题
质量约束
背包问题也是一道经典的动态规划问题,它有许多表述形式,什么劫匪小偷抢超市啦,出去旅行要打包啦,简单来说,背包问题给出了一序对集合 \(R^n=\{t_i=(w_i, v_i)\mid i=1,2,,,n\}\) ,其中 \(w_i\) 是物品总重量,\(v_i\) 是物品价值,要求从中选取总重量不超过 \(W\) 的物品,使得物品总价值 \(V\) 尽可能的大。
由于上述问题中有 \(n\) 件物品,所以将该问题定义为 \(Q^n\),假设 \(V^n\) 是该问题最优解的总价值,显然 \(V^n\) 的值与 \(R^n\) 和 \(W\) 都相关,即
\[V^n = f(W, R^n)\]现在我们稍微缩小问题的规模,若已经从物品列表中拿取了 \(t_j\),并从限定总重量中减去该物品的重量 \(w_j\),然后在剩下的物品 \(R^n\setminus t_j\) 中再取总重量不超过 \(W-w_j\) 的物品,此时的问题用符号 \(Q^{n-1}_j\) 表示,下标 \(j\) 表示排除的物品序号,于是我们便得到一系列子问题
\[Q_1^{n-1},Q_2^{n-1},Q_3^{n-1},,,Q_n^{n-1}\]对于问题 \(Q_j^{n-1}\) ,设它的最优解为集合 \(S_j^{n-1}\) ,显然 \(S_j^{n-1}\subset R^n\setminus t_j\) ,并且总价值为
\[V_j^{n-1} = f(W-w_j, R^n\setminus t_j)\]假设问题 \(Q^n\) 的最优解为集合 \(S^n\) ,下面我们将证明,必然存在某一个 \(j = k\) 使得 \(S^n = S_k^{n-1} \cup t_k\) 。
这里我们使用反证法,假设对于任意 \(1\le j\le n\) 都不存在 \(S^n = S_j^{n-1} \cup t_j\) ,即 \(S^n \setminus t_j\) 不是问题 \(Q_j^{n-1}\) 的最优解,那么则有两种情况,即
1、\(S^n \setminus t_j\) 的总价值比 \(S_j^{n-1}\) 的更小,此时 \(S_j^{n-1} \cup t_j\) 将是问题 \(Q^n\) 更好的解。
2、\(S^n \setminus t_j\) 的总重量比 \(W-w_j\) 更大,此时 \(S^n\) 的总重量将超过 \(W\)。
也就是说上述两种情况都与 \(S^n\) 是最优解的事实相违,于是从反方向证明了前面的论断。从而我们找到了该问题的最优子结构,即 \(Q^n\) 的最优解可以从它的某个子问题 \(Q_j^{n-1}\) 的最优解得到。
\[f(W, R^n) =\max_j\,\, \left(f(W-w_j, R^n\setminus t_j) + v_j\right)\]下图显示了当 \(n=3\) 时的各层次问题组成的树形结构
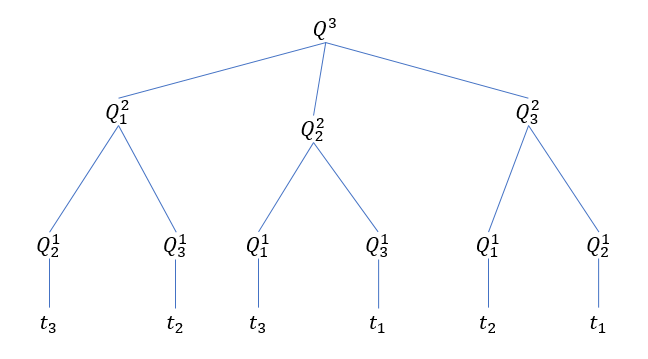
对于任意的 n ,我们将得到一个深度为 n 的树形递归结构,它的根节点有 n 个子节点,第二层节点有 n-1 个子节点,以此类推,如果要完全搜索整棵树,那么时间复杂度将是 \(n!\) 。
但事实上,我们不必完全求解所有子问题,举个简单的例子,假如物品 \(t_m\) 在所有物品中具有最小的重量以及最高的价值,那么首先选取该物品是最明智的,于是我们只需计算第二层节点中的问题 \(Q_m^{n-1}\) 。另一方面,如果物品 \(t_r\) 具有最大的重量,以及最小的价值,那么我们在这轮选择中就可以不用计算 \(Q_r^{n-1}\) ,因为选择它显然有点得不偿失。虽然这些只是理想的情况,因为很可能不存在这样的物品,但这给我们以启发,即,可以通过物品之间的重量和价值关系来判断是否有必要在本轮选择中计算相应的子问题。
那么具体的判断规则是怎样的呢?我们可以将所有物品按价值从高到低进行排序,然后以最后一个物品 \(t_n\) 为基准向前搜索,一旦发现某个物品 \(t_j\) 的重量小于 \(t_n\) 或者大于\(W\),那么我们就排除问题 \(Q_n^{n-1}\) ,当然这并不是说 \(t_n\) 就被我们永久屏蔽了,而是当前有明显比它更好的选择。接着以 \(t_{n-1}\) 为基准向前搜索,直到 \(n=1\)。
这一过程的伪码为
func remove_problem_list(items)
remove_list = [];
sort(items);
n = items.length;
for i: n -> 1
base_weight = items[i].weight;
for j: i -> 1
if items[j].weight < base_weight
remove_list.append(items[i]);
break;
end
end
end
return remove_list;
end
还是以 n = 3 的情况来举例说明,假设这三个物品的重量和价值如下所示
\[t_1=(10, 5)\\t_2=(4,20)\\t_3=(6,25)\]并且重量限制 \(W = 15\)。于是我们看到第一轮选择中,\(t_1\) 是明显可以被排除的,这就相当于修剪掉了前面树形结构中的 \(Q_1^2\) 分支,它的后续子问题也就自然排除。它的整个运行过程如下所示
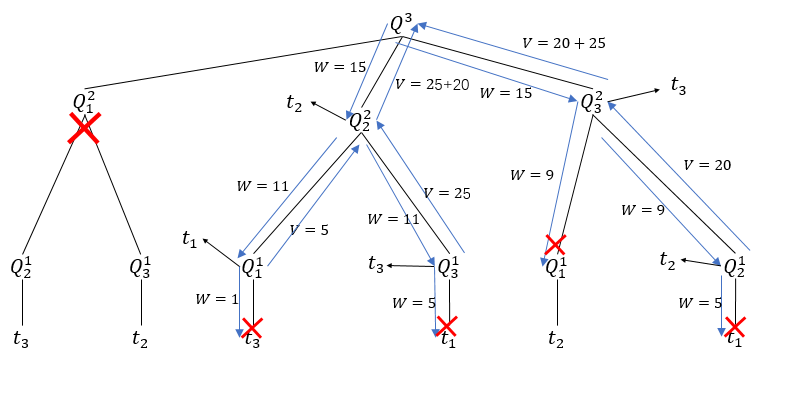
看起来这就是对树的深度优先搜索,在每个节点都会比较它的子节点返回的价值大小,并向其父节点返回较大的那一个。写成递归过程如下
func solve(W, items)
## 处理平凡情况
if items.length == 1
if items[0].weight <= W
return items[0].value;
else
return 0;
end
end
remove_problem_list = remove_problem_list(items);
select_item_list = item not in remove_problem_list;
values = [];
for item in select_item_list
values.append(solve(W - item.weight, items except item) + item.value);
end
return max in values;
end
上述方案只解决了问题的一部分,即能够取得物品的最大总价值,却没有给出该选择哪些物品。当然这也很好办,只需要让递归函数返回最优的路径即可,该路径就是已经选择的物品列表。伪码如下
func solve(W, items)
## 处理平凡情况
if items.length == 1
if items[0].weight <= W
return items;
else
return [];
end
end
remove_problem_list = remove_problem_list(items);
select_item_list = items not in remove_problem_list;
candicate_items_list = [];
for item in select_item_list
candicate_items_list.append(solve(W - item.weight, items except item).append(item));
end
return candicate_items in candicate_items_list which have max value
end
下面我们用 Java 实现来做一个具体的例子,原理和上面的伪码差不多
//定义物品类 Item
class Item{
int w;
int v;
Item(int w, int v) {
this.w = w;
this.v = v;
}
public String toString(){
return w+":" +v;
}
}
//移除不必要问题的方法
private List<Item> removeProblemList(List<Item> items, int W) {
ArrayList<Item> remove = new ArrayList<>();
for(int i = items.size() - 1; i >= 0; i--) {
Item base = items.get(i);
if(base.w > W) {
remove.add(base);
}else{
for(int j = i - 1; j >= 0; j--) {
if(base.w > items.get(j).w) {
remove.add(base);
break;
}
}
}
}
return remove;
}
//递归调用方法
public List<Item> solve(int W, List<Item> items) {
if(W <= 0) {
return new ArrayList<>();
}
if(items.size() == 1) {
if(items.get(0).w <= W) {
ArrayList<Item> candicate = new ArrayList<>();
candicate.add(items.get(0));
return candicate;
}else{
return new ArrayList<>();
}
}
List<Item> remove = removeProblemList(items, W);
//待求解问题
List<Item> selects = items.stream()
.filter(item -> !remove.contains(item))
.collect(Collectors.toList());
ArrayList<List<Item>> candicate_items_list = new ArrayList<>();
for (Item select : selects) {
List<Item> remain = items.stream().filter(item -> item != select).collect(Collectors.toList());
List<Item> result = solve(W - select.w, remain);
result.add(select);
candicate_items_list.add(result);
}
//从候选列表中找到具有最大价值的物品路径
int max = 0;
int max_index=0;
for (int i = 0; i < candicate_items_list.size(); i++) {
int value = candicate_items_list.get(i).stream().mapToInt(item -> item.v).sum();
if(value > max){
max = value;
max_index = i;
}
}
return candicate_items_list.get(max_index);
}
测试:
@Test
public void testKP() {
Item[] items = {new Item(3,4),new Item(3,4),new Item(3,4),
new Item(8, 5),new Item(8, 5),new Item(2, 2),new Item(2, 2),
new Item(5, 3),new Item(20, 11)};
sort(items);
int W = 60;
List<Item> solution = solve(W, Arrays.asList(items));
System.out.println(solution);
//output: [2:2, 2:2, 5:3, 3:4, 3:4, 3:4, 8:5, 8:5, 20:11]
}
体积约束的讨论
背包问题有很多变种,比如除了质量限制外,我们还可以限制体积,也就是说给每个物品再增加一个体积属性,然后在质量和体积不超过预设的条件下,挑选价值尽可能大的物品组合。
其实增加一个约束并不会对我们要求解问题的树形结构产生根本性改变,只不过是在每个子问题中增加了一个类似对质量的处理步骤。让我们回顾一下,我们是怎样处理质量的,在问题 \(f(W, R^n)\) 中, 首先从 \(R^n\) 中挑选出 \(t_i\) ,然后从约束质量 \(W\) 中减去 \(w_i\) ,便获得子问题 \(f(W-w_i, R^n\setminus t_i)\) 。
现在我们增加体积约束,这时的问题变成 \(f(W, Vol, R^n)\) ,其中 \(Vol\) 表示约束体积,当我们选出物品 \(t_i\) 时,子问题不仅要减去质量 \(w_i\) ,还应该减去 \(vol_i\) ,即物品 \(t_i\) 的体积。
然后再来看一下子问题修剪的方法,前面我们在挑选子问题时排除了质量和价值均不占优的物品,也就是那些质量偏大,价值偏小的物品。那么对于体积也应该同样处理,只不过这应该和质量配合起来,也就是说,质量、体积和价值均不占优势的物品才应该被排除,只要有一个属性有优势,就不应该排除。至于为何应该如此,我觉得可以通过一个简单的例子来说明,假如有两个物品,其质量、体积和价值分别为 \((10, 20, 5)\) 和 \((5, 10, 3)\) ,定义约束为 \(W = 20, V = 20\) ,那么此时应该选质量和体积都不占优的第一个物品。