反向传播算法
本文的符号约定来自于 Andrew Ng 的 cs294a,推导过程参考边肇祺的《模式识别 第二版》。
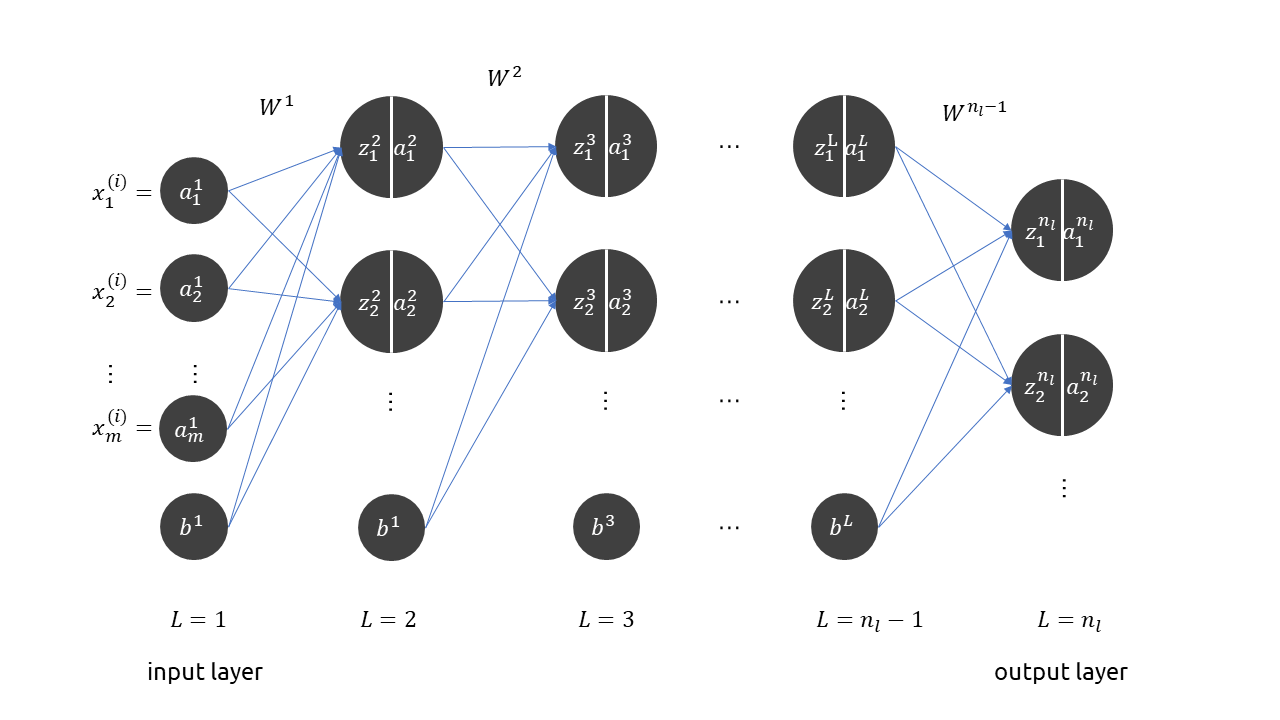
上图是一个典型的前馈网络结构,定义训练集
\[S = \{(x^{(i)}, y^{(i)}) \mid i = 1,,,m\}\]定义权重矩阵集,和偏置项集
\[W = \{W^i \mid i = 1,,,n_l\}, b = \{b^i\mid i = 1,,,n_l\}\]图中隐藏层和输出层的单元被分隔成两部分,其中左边部分的 \(z^l\) 代表前一层单元的加权值
\[z^{l+1} = W^l a^l + b^l\]右边的 \(a^l\) 则代表本单元的激活值
\[a^{l+1} = f(z^{l+1})\]其中 \(f\) 为激活函数。在输入层有 \(a^1 = x^{(i)}\),这里的 \(i\) 代表样本编号。通过层层传递,在最后一层输出 \(a^{n_l}\),假设整个神经网络为黑箱函数 \(h_{W,b}(x)\),那么
\[a^{n_l} = h_{W,b}(x)\]定义单个样本损失函数
\[J(W, b; x, y) = \frac 1 2 \parallel h_{W, b}(x) - y \parallel^2\]总体损失函数
\[J(W, b) = \frac 1 m \sum_{i=1}^m J(W, b;x^{(i)}, y^{(i)}) + \frac {\lambda} 2 \sum_{l=1}\sum_{i=1}\sum_{j=1} \left(W_{ij}^{l}\right)^2\]其中 \(\frac {\lambda} 2 \sum_{l=1}\sum_{i=1}\sum_{j=1} \left(W_{ij}^{l}\right)^2\) 是正则项,\(\lambda\) 为正则化系数。
为了求解优化问题
\[\min_{W, b} J(W, b)\]可以利用梯度下降优化算法,迭代公式为
\[\begin{aligned} W_{ij}^l &= W_{ij}^l - \alpha \frac{\partial }{\partial W_{ij}^l} J(W, b)\\ b_i^l &= b_{i}^l - \alpha \frac{\partial }{\partial b_i^l} J(W, b) \end{aligned}\]这里的 \(l\) 代表任意层,为了计算损失函数对任意层权重矩阵的梯度,下面我们按步骤讨论著名的反向传播算法:
1、 前馈计算每一层的激活值 \(a^l\),直到最后一层 \(a^{n_l}\)。
2、 设最后一层与倒数第二层的权重矩阵为 \(W^{n_l-1}\),计算总体损失函数对各权重参数的偏导数
\[\begin{aligned} \frac{\partial}{\partial W_{ij}^{n_l-1}} J(W, b) &= \frac{\partial J}{\partial a_j^{n_l}} \frac{\partial a_{j}^{n_l}}{\partial z_j^{n_l}}\frac{\partial z_j^{n_l}}{\partial W_{ij}^{n_l-1}}\\ &=\frac 1 2\frac{\partial}{\partial a_j^{n_l}} \parallel a_j^{n_l} - y^{(j)} \parallel^2 \cdot f'(z_j^{n_l}) \cdot \frac{\partial }{\partial W_{ij}^{n_l-1}} \left( \sum_{k} W_{kj}^{n_l-1} a_{k}^{n_l-1} +b^{n_l-1} \right)\\ &=(a_j^{n_l} - y^{(j)}) f'(z_j^{n_l}) a_i^{n_l-1} \end{aligned}\]3、 设倒数第二层与倒数第三层的权重矩阵为 \(W^{n_l-2}\),计算总体损失函数对各权重参数的偏导数
\[\frac{\partial}{\partial W_{ij}^{n_l-2}} J(W, b) = \frac{\partial J}{\partial z_{j}^{n_l-1}} \frac{\partial z_j^{n_l - 1}}{\partial W_{ij}^{n_l - 2}} = \frac{\partial J}{\partial z_{j}^{n_l-1}} a_{i}^{n_l-2}\]其中
\[\begin{aligned} \frac{\partial J}{\partial z_{j}^{n_l-1}} &= \sum_{k=1}\frac{\partial J}{\partial z_{k}^{n_l}}\frac{\partial z_{k}^{n_l}}{\partial z_{j}^{n_l - 1}}\\ &=\sum_{k=1} \frac{\partial J}{\partial a_{k}^{n_l}} \frac{\partial a_{k}^{n_l}}{\partial z_{k}^{n_l}} \cdot \frac{\partial z_{k}^{n_l}}{\partial a_{j}^{n_l - 1}} \frac{\partial a_{j}^{n_l - 1}}{\partial z_{j}^{n_l - 1}}\\ &=\sum_{k=1}(a_k^{n_l} - y^{(k)}) f'(z_k^{n_l}) W_{jk}^{n_l - 1} f'(a_j^{n_l-1}) \end{aligned}\]于是
\[\frac{\partial}{\partial W_{ij}^{n_l-2}} J(W, b) =\sum_{k=1}(a_k^{n_l} - y^{(k)}) f'(z_k^{n_l}) W_{jk}^{n_l - 1} f'(a_j^{n_l-1})a_{i}^{n_l-2}\]4、 定义\(\delta_{i}^{n_l}=(a_i^{n_l} - y^{(i)})f’(z_i^{n_l})\), 那么
\[\frac{\partial}{\partial W_{ij}^{n_l-1}} J(W, b) = \delta_{j}^{n_l} a_i^{n_l-1}\] \[\frac{\partial}{\partial W_{ij}^{n_l-2}} J(W, b) = \sum_{k=1}\delta_{k}^{n_l} W_{jk}^{n_l - 1} f'(a_j^{n_l-1})a_{i}^{n_l-2}\]若再定义 \(\delta_j^{n_l-1} = \sum_{k=1}\delta_{k}^{n_l} W_{jk}^{n_l - 1} f’(a_j^{n_l-1})\), 那么则有
\[\frac{\partial}{\partial W_{ij}^{n_l-2}} J(W, b) =\delta_j^{n_l-1} a_{i}^{n_l-2}\]于是可以归纳,对于任意的层 \(l\)
\[\frac{\partial J}{\partial W_{ij}^l} = \delta_{j}^{l+1}a_i^l\]并且
\[\delta_j^l = \sum_{k=1}\delta_{k}^{l+1} W_{jk}^l f'(a_j^l)\]通过上述步骤,我们看到,通过计算后一层的 \(\delta^{l+1}\) ,可以得到前一层的 \(\delta^l\) 以及 \(\frac J{W_{ij}^l}\),并且层层向前传播,刚好与前馈计算的方向相反,这也是反向传播算法名称的由来。