模式识别中的最小错误率分类决策
对于一个有监督的分类学习问题,如果我们把注意力仅集中在分类的对错上面,就自然会想到使用一个函数来度量分类的错误率,并且在学习的过程中尽量减小训练数据的分类错误率,这就是基于最小错误率的决策方法。
假设我们拿到了一组特征数据及其类别标签
\[S = \{(x_i, y_i)\mid i\in N^+, i\le n ,\, \,y_i \in \{\mathcal{C}_j\},\,j=1,2,,,k\}\]也就是说,总共有 n 个特征,它们分属于 k 个类别。如果特征的维度是 d ,那么可以认为特征空间是一个 d 维实向量空间 \(R^d\) 的子集。分类行为其实就是在计算一个从特征空间到类别集合的映射,我们定义该映射如下
\[f:R^d \rightarrow C\]这里的 \(C = {\mathcal{C}_i}\, , i = 1,2,,,k\) 。由于 d 维实向量空间本身就是一个群(既是加法群,又是乘法群)。所以我们可以在其中定义等价关系,即:
如果 \(x_i\) 和 \(x_j\) 都被映射到同一个类别:\(f(x_i)=f(x_j)\) ,那么两者等价。
可以看到,这个关系满足自反性,对称性以及传递性,所以这确实是一个等价关系。于是特征空间可以通过这一等价关系被划分成 n 个等价类,定义为 \(R_i\,,\,i = 1,2,,,n\),它们都是特征空间的子集,但互不相交,且有
\[f(x \in R_i) = \mathcal{C}_i\]对于一个特征 \(x\),我们对它进行分类的过程其实就是计算 \(f(x)\) ,看结果属于哪一类别,所以 \(f(x)\) 就代表我们的预测结果,它和特征的实际类别属性不是一个概念,但却相关,定义两者的联合分布为
\[p(f(x), \mathcal{C}_j)\]其中 \(f(x)=\mathcal{C}_i\) ,这里的 i 是与 j 独立的量。显然,要使 \(f(x)=\mathcal{C}_i\) ,则必然有 \(x \in R_i\),反之亦然,所以上面定义的联合分布又等价于
\[p(x\in R_i, \mathcal{C}_j)\]如果分类正确,那么就必须使得 \(i=j\) ,所以将一个特征分类到 \(\mathcal{C}_i\) 并且还正确的概率就为
\[p(x\in R_i, \mathcal{C}_i) = \int_{x\in R_i} p(x, \mathcal{C}_i)\mathbf{d}x\]将二元组 \((x\in R_i, \mathcal{C}_i)\) 作为一个事件,那么我们可以定义正确分类的事件为如下形式
\[\bigcup_{i=1}^n (x\in R_i, \mathcal{C}_i)\]由于上述事件的互斥性,于是正确分类的概率就为
\[\begin{aligned} p(correct) &= p\left(\bigcup_{i=1}^n (x\in R_i, \mathcal{C}_i)\right) \\ &= \sum_{i=1}^n p(x\in R_i, \mathcal{C}_i) \\ &= \sum_{i=1}^n \int_{x\in R_i} p(x, \mathcal{C}_i)\mathbf{d}x \end{aligned}\]可以看到,这个概率的值与特征空间划分方式有关,那么怎样的划分才能使上述函数取到最大值呢?为了简单起见,考虑一维特征空间下的联合分布函数 \(p(x, \mathcal{C}_i)\) 图像
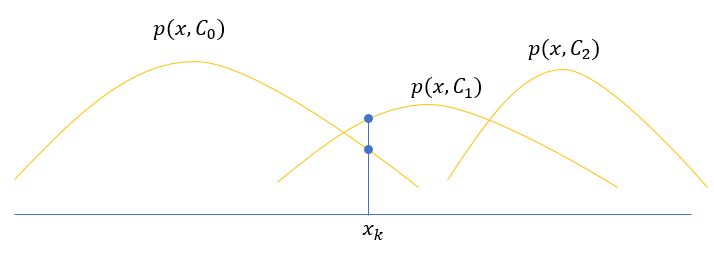
以图中的点 \(x_k\) 举例,如果 \(x_k \in R_0\) ,那么在计算积分的时候,其对应的被积函数值为 \(p(x_k, \mathcal{C}_0)\),而如果 \(x_k \in R_1\) ,那么相应的被积函数值为 \(p(x_k, \mathcal{C}_1)\),由于 \(p(x_k, \mathcal{C}_1) > p(x_k, \mathcal{C}_0)\) ,所以为了使 \(p(correct)\) 尽量大,最好的划分方式就是令 \(x_k \in R_1\)。
通过上面的分析可知,要使正确率尽量大,可以先计算联合分布 \(p(x,\mathcal{C}_i),\,\,i=1,2,,,n\) ,找到其中的最大值,然后将 \(x\) 归入相应的类别。考虑到
\[p(x,\mathcal{C}_i) = p(\mathcal{C}_i \mid x)p(x)\]其中 \(p(\mathcal{C}_i \mid x)\) 为知晓特征 \(x\) 后,进行分类的后验概率,由于 \(p(x)\) 对于所有 \(x\) 来说是一样的,所以最大的 \(p(x,\mathcal{C}_i)\) 等价于最大的后验概率 \(p(\mathcal{C}_i\mid x)\) 。另一方面,又有
\[p(x,\mathcal{C}_i) = p(x\mid \mathcal{C_i})p(\mathcal{C}_i)\]这里的 \(p(x\mid \mathcal{C}_i)\) 是已知类别条件下的特征概率密度函数,\(p(\mathcal{C}_i)\) 是类别的先验概率,通过这两个值同样能计算出联合分布。
再定义错误率
\[p(error) = 1 - p(correct)\]于是最大化正确率就等价于最小化错误率。