MKL 向量统计库 VSL 中的数据存储与索引风格的应用
由于 MKL 支持两种数据存储方式,在使用 VSL 进行统计计算的时候,可以使用参数 VSL_SS_MATRIX_STORAGE_ROWS 和 VSL_SS_MATRIX_STORAGE_COLS 来指定我们传入的数据布局为行存储或者列存储。但是我们一般习惯的是类 C 语言的行索引风格,所以这篇文章就来讨论一下如何使用 VSL 这两种风格的适当组合来适配计算矩阵的统计量。
一些约定
在写这篇文章的时候我发现很多概念模棱两可,如果不提前做好约定,不仅会让读者不知所云,也让我的思路很乱。这里我先把之后要用到的数据拿出来
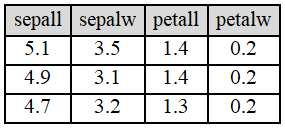
这是著名的鸢尾花数据集,为了简便起见,我就只取了前三个样本。当我们要把这堆数据放到程序中的时候,自然会考虑用二维数组来存储
\[\left[ \begin{aligned} 5.1\quad\quad& 3.5& 1.4\quad\quad& 0.2\\ 4.9\quad\quad& 3.1& 1.4\quad\quad& 0.2\\ 4.7\quad\quad& 3.2& 1.3\quad\quad& 0.2 \end{aligned} \right]\]我把类似这种形式的表示称为数据的 二维数组视图。但我们知道二维数组在内存中其实是一维的,特别是在 C 语言中,子数组之间也没有空隙,于是我们把它的一维表示形式称为数据的 内存视图。
\[[5.1\quad 3.5\quad 1.4\quad 0.2\quad 4.9\quad 3.1\quad 1.4\quad 0.2\quad 4.7\quad 3.2\quad 1.3\quad 0.2]\]可以发现,内存视图其实就是把二维数组视图的每个子数组拼接起来形成的,或者说是对二维数组视图按行遍历形成了内存视图。这就启发我们考虑按列遍历二维数组会得到什么?
\[[5.1\quad 4.9\quad 4.7\quad 3.5\quad 3.1\quad 3.2\quad 1.4\quad 1.4\quad 1.3\quad 0.2\quad 0.2\quad 0.2]\]其实这也可以看作一个内存视图。也就是说,一个二维数组视图,通过两种遍历方式可以得到两种不同的内存视图。这里我们把对二维数组的按行遍历或者按列遍历统称为 遍历方向。
而反过来,从内存视图恢复二维数组视图则要稍微复杂点,首先必须要指定二维数组视图的行数和列数,一般称为 形状,然后还需要指定是按列恢复还是按行恢复,比如从 1 到 10 的连续整数列表
\[[1\quad 2\quad 3\quad 4\quad 5\quad 6\quad 7\quad 8\quad 9\quad 10]\]若假设二维数组视图的形状为 2行 5列,并且按行连续(这里的连续指的是在内存视图中连续),则从内存视图恢复得到的二维数组为
\[\left[\begin{aligned} &1\quad 2\quad 3\quad 4\quad 5\quad \\ &6\quad 7\quad 8\quad 9\quad 10 \end{aligned} \right]\]若按列连续恢复,则相应的二维数组为
\[\left[\begin{aligned} &1\quad 3\quad 5\quad 7\quad 9\quad \\ &2\quad 4\quad 6\quad 8\quad 10 \end{aligned} \right]\]而如果二维数组视图的形状为 5行 2列,那么按行连续恢复时
\[\left[\begin{aligned} &1\quad 2\\& 3\quad 4\\&5\quad 6\\ & 7\quad 8\\& 9\quad 10 \end{aligned} \right]\]按列连续恢复时
\[\left[\begin{aligned} &1\quad 6\\ &2\quad 7\\ &3\quad 8\\ &4\quad 9\\ &5\quad 10 \end{aligned} \right]\]我们这里把按行连续恢复或者按列连续恢复统称为 恢复方向。可以看到,同一段内存视图,根据数组形状或恢复方向的不同,能得到多种不同的二维数组视图。
通过以上分析,我们总结出,要从二维数组视图得到明确的内存视图,需要约束遍历方向,而反过来得话,则需要约束恢复方向和形状两个参数。
从另一个方面来看,从二维数组视图到内存视图,是一种存储过程,而从内存视图到二维数组视图,则是一种按索引读取过程。所以遍历方向和恢复方向又分别可以看作存储风格和索引风格,即二维数组视图按行遍历得到内存视图,是行存储风格,按列则是列存储风格,内存视图按行恢复得到二维数组视图,是行索引风格,按列恢复则是列索引风格。
使用 VSL 统计计算
向量统计库设计了一套完整的任务流程API,大致分成三个阶段:新建任务,编辑任务以及计算,分别对应于三个函数 vsl*NewTask, vsl*EditTask,vsl*SSCompute 其中的 * 号可以取 d s i 分别代表双精度浮点数、单精度浮点数以及整数。
现在考虑使用 VSL 计算前面给的鸢尾花数据的一些统计值,来探讨它的内部处理方式,首先我们把数据按行遍历写到一维数组中(即内存视图)
double matrix[] = {5.1, 3.5, 1.4, 0.2, 4.9, 3.1, 1.4, 0.2, 4.7, 3.2, 1.3, 0.2};
然后指定二维数据视图的形状为 3行 4列(这与我们的原始数据相同)
MKL_INT ROW = 3;
MKL_INT COL = 4;
以及从二维数组视图到内存视图的存储方式为行存储
MKL_INT x_storage = VSL_SS_MATRIX_STORAGE_ROWS;
由于还不知道 VSL 内部处理行列风格的原理,我们先做一下实验,完整代码如下
//main.c
#include <stdio.h>
#include "mkl.h"
int main()
{
/* 数组定义 \*/
double matrix[] = {5.1, 3.5, 1.4, 0.2, 4.9, 3.1, 1.4, 0.2, 4.7, 3.2, 1.3, 0.2};
MKL_INT ROW = 3;
MKL_INT COL = 4;
MKL_INT x_storage = VSL_SS_MATRIX_STORAGE_ROWS;
VSLSSTaskPtr task;
double mean[COL];
int errcode;
unsigned MKL_INT64 estimate = VSL_SS_MEAN;
// 新建任务:导入数组描述
errcode = vsldSSNewTask( &task, &ROW, &COL, &x_storage, (double*)matrix, 0, 0 );
// 编辑任务:设定任务为均值计算
errcode = vsldSSEditTask( task, VSL_SS_ED_MEAN, mean);
// 开始计算任务
errcode = vsldSSCompute( task, estimate, VSL_SS_METHOD_FAST );
printf("%f,%f,%f,%f\n",mean[0], mean[1],mean[2],mean[3]);
// 释放资源
errcode = vslSSDeleteTask( &task );
MKL_Free_Buffers();
return errcode;
}
/*
compile command:
gcc -c main.c -o target.o -I "%MKL_ROOT%\include"
gcc -o target.exe target.o -L "%MKL_ROOT%\lib\intel64_win" -lmkl_rt
*/
//2.550000,2.400000,2.350000,0.000000
上述代码是想计算矩阵中的行或列的均值,但是由于不知道 VSL 实际会计算行的均值还是列的均值,所以我们令数组 mean 的长度为较大的那一个,即 COL。通过结果我们看到,它计算的是行均值。
结合我们的参数设定,可以猜想,上述代码计算的是:依据形状和存储风格,从内存视图中恢复出来的二维数组视图的行均值。
 (数据变换流程)
(数据变换流程)
既然如此,我们就可以进一步猜想,要计算某一矩阵的列均值,只需要让 VSL 中的二维数组视图是原始矩阵的转置即可。但是这里还有一个不清楚的地方,我们指定矩阵的存储方式那行代码
MKL_INT x_storage = VSL_SS_MATRIX_STORAGE_ROWS;
它是作用在哪个位置的?是从概念形式到代码形式那里,还是从代码形式到 VSL 那里?或者两者皆有?
如果它是作用在概念形式到代码形式那里的话,那么只要改变 x_storage 的值,我们的 matrix 数组就必须变化,因为概念形式是固定的,行存储或列存储得到的内存视图就会不一样。
然而 matrix 数组是否能够随意变化呢?这就要看 matrix 数组是从哪里来的了。很明显,matrix 数组是我们自己给的,如果有一个函数 mean(),那么 matrix 就是其中一个参数,如果它在 mean 函数内部转置一次,那为何我们不在函数外部对它转置再传进来,偏偏要增加 mean 函数的计算开销。所以我们不希望 matrix 在这里发生任何变化。
于是可以认为 x_storage 是作用在代码形式—— VSL 过程,但如果是顺序过程的话,根据我们的定义,它是一个索引过程,是存储过程的逆过程,所以我认为 x_storage 是作用在 VSL 到代码形式这一过程的。补全的数据变换图如下所示

通过以上分析,我们再来看矩阵列均值的计算就会清晰很多,首先可以画出它的数据变换图

具体代码与前面类似,只不过交换了 ROW 与 COL 的值,并将 x_storage 修改成了 VSL_SS_MATRIX_STORAGE_COLS。
int main(){
/* 数组定义 \*/
double matrix[] = {5.1, 3.5, 1.4, 0.2, 4.9, 3.1, 1.4, 0.2, 4.7, 3.2, 1.3, 0.2};
MKL_INT ROW = 4;
MKL_INT COL = 3;
MKL_INT x_storage = VSL_SS_MATRIX_STORAGE_COLS;
VSLSSTaskPtr task;
double mean[ROW];
int errcode;
unsigned MKL_INT64 estimate = VSL_SS_MEAN;
// 新建任务:导入数组描述
errcode = vsldSSNewTask( &task, &ROW, &COL, &x_storage, (double*)matrix, 0, 0 );
// 编辑任务:设定任务为均值计算
errcode = vsldSSEditTask( task, VSL_SS_ED_MEAN, mean);
// 开始计算任务
errcode = vsldSSCompute( task, estimate, VSL_SS_METHOD_FAST );
printf("%f,%f,%f,%f\n",mean[0], mean[1],mean[2],mean[3]);
// 释放资源
errcode = vslSSDeleteTask( &task );
MKL_Free_Buffers();
return errcode;
}
//output: 4.900000,3.266667,1.366667,0.200000
更好的方法是将均值计算过程提取成函数,它的参数应该被精心设计,首先应该能传递矩阵的数据,也就是一个数组指针,然后还应该让我们知道矩阵的行列数,以及一个标志用来表示我们需要按行或者按列计算,当然还有一个指针用来存储计算结果。它看起来应该是下面这样的
int mean(double* matrix, int ROW, int COL, int axis, double* m);
实现代码如下
int mean(double* matrix, int ROW, int COL, int axis, double* m) {
VSLSSTaskPtr task;
MKL_INT x_storage = (axis == 0)?VSL_SS_MATRIX_STORAGE_ROWS:VSL_SS_MATRIX_STORAGE_COLS;
if(axis != 0) {
int temp = ROW;
ROW = COL;
COL = temp;
}
int errcode;
unsigned MKL_INT64 estimate = VSL_SS_MEAN;
errcode = vsldSSNewTask( &task, &ROW, &COL, &x_storage, (double*)matrix, 0, 0 );
errcode = vsldSSEditTask( task, VSL_SS_ED_MEAN, m);
errcode = vsldSSCompute( task, estimate, VSL_SS_METHOD_FAST );
errcode = vslSSDeleteTask( &task );
MKL_Free_Buffers();
return errcode;
}
在应用的时候,我们按照实际情况设置矩阵的 ROW 和 COL
double matrix[] = {5.1, 3.5, 1.4, 0.2, 4.9, 3.1, 1.4, 0.2, 4.7, 3.2, 1.3, 0.2};
int ROW = 4;
int COL = 3;
double m[ROW];
然后调用函数,如果要计算每行的均值,令 axis = 0,否则计算每列的均值。
mean(matrix, ROW, COL, 0, m);
printf("%f,%f,%f,%f\n",m[0], m[1],m[2],m[3]);
// output: 2.550000,2.400000,2.350000
mean(matrix, ROW, COL, 1, m);
printf("%f,%f,%f\n",m[0], m[1],m[2]);
// output: 4.900000,3.266667,1.366667,0.200000
总结
这篇文章的讨论稍微会有点绕,因为可变的因素实在太多,比如矩阵的存储风格,索引风格,行和列,转置之后的行和列,以及 VSL 对数组的处理方式等等,我们需要精心定义概念才不至于把自己搞懵。但是最终的结论很简单,如果要计算矩阵的行方向统计量(比如均值,方差等),则 ROW 和 COL 的值与矩阵的行与列匹配,存储方式设为行存储。如果要计算列方向上的统计量,则 ROW 和 COL 的值应该交换,并把存储方式设为列存储。