理解主成分分析（1）——最大方差投影与数据重建
一方面，高维数据的存储和计算对计算机的性能提出了更高的要求，另一方面，对于人来讲，高维数据提供的信息不太直观，所以如何对数据进行降维一直是一项很有意义的话题。
最大方差投影与主成分
让我们先从一个二维数据集开始，设
\[S = \{x_i\mid x_i \in R^2 , i=1,2,,,n\}\]把上述点集画到平面上，假设产生了下面的图像
现在我们想要为每个点赋予一个具有代表性的值来替代它的坐标，从而降低该数据集的维度，并且这个被赋予的值应该在最大程度上表现出被它替代的点的特征。那什么是点的特征呢？对于一个点来讲，与其他点的不同就是它所拥有的特征，所以如果它的替代值能尽可能地与其他点的替代值相异，那么这种替换就是有意义的。当然，这种降维方式损失了不少信息，但我们先不管这个。一个想法是，将点投影到坐标轴上，然后用坐标轴上的值作为点的替代值，如下面显示的图像
前一张的图像以横轴作为投影直线，后一张以纵轴为投影直线。不难发现，将点集投影到横轴上具有更强的分散性，即点与点的区分度越大。那么怎样来衡量这种区分度呢？我们很自然地会想到方差，显然方差越大越好，上述数据的横坐标方差大于纵坐标方差，所以如果非要对点集 \(S\) 进行降维，那么把它们投影到横轴上比投影到纵轴上要更合理一点。这样一来我们得到了一个新的数据集合，它是由原数据集的所有横坐标组成的。
但是现在有一种情况，那就是给定另外一数据集，如果坐标轴（无论是横轴还是纵轴）不是数据的最佳投影轴，如下图所示，事实上，此时最佳投影轴是斜率为1的直线
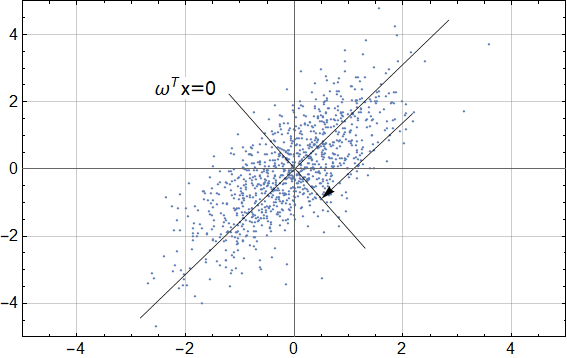
此时就不能单纯的用点的横纵坐标值来替代了，一种可行的方案是，先把点投影到斜率为 1 的直线上，然后计算投影点与原点的带符号距离，这个带符号距离就最佳的替代值。但其实找到这个值不用这么麻烦，考虑一条与上述投影线相垂直的直线，假设它的方程为
\[\omega^T x = 0\]其中令 \(\mid \omega\mid=0\) ，容易证明
\[f(x) =\omega^T x\]其实就是点 \(x\) 到直线 \(\omega^T x = 0\) 的带符号距离。所以从另一个角度来看，将点映射成它到某直线的带符号距离也是一种降维方法，并且和投影方法是等价的，前者的优势在于计算更简单。
当拿到样本数据集之后，一开始并不知道具体的目标直线，所以只有任意构造一条直线，然后计算得到一系列带符号距离
\[Y = [y_1 \quad y_2 \quad\cdots \quad y_n]\]其中 \(y_i=f(x_i)\)。于是我们的目标其实就是寻找 \(\omega\) 使得 \(Var(Y)\) 具有最大值。为了一般性讨论，我们考虑更高维的数据，假设特征维度为 d ，那么
\[y_i =\omega^T x_i = \omega_1 x_{i1} + \omega_2 x_{i2} + ... + \omega_d x_{id}\]写成矩阵形式为
\[Y = \left[ \begin{aligned} y_1 \\y_2\\\vdots\\y_n \end{aligned} \right] =\omega_1\left[ \begin{aligned} x_{11} \\x_{21}\\\vdots\\x_{n1} \end{aligned} \right] + \omega_2\left[ \begin{aligned} x_{12} \\x_{22}\\\vdots\\x_{n2} \end{aligned} \right] + ... + \omega_d\left[ \begin{aligned} x_{1d} \\x_{2d}\\\vdots\\x_{nd} \end{aligned} \right]\]如果再定义
\[X_i = \left[ \begin{aligned} x_{1i} \\x_{2i}\\...\\x_{ni} \end{aligned} \right]\]那么就有
\[Y =\omega \cdot X = \sum_{i=1}^d \omega_i X_i\]我们在这里将所有特征点作为一个矩阵来考虑，即
\[X = [X_1 \quad X_2 \quad ...\quad X_d]\]然后假设其协方差矩阵为
\[\Sigma = \left[ \begin{aligned} \sigma_{11}\quad&\sigma_{12}\quad..&\sigma_{1d} \\ \sigma_{21}\quad&\sigma_{22}\quad..&\sigma_{2d}\\ ..\quad&..\,\,\,\quad..&..\\ \sigma_{d1}\quad&\sigma_{d2}\quad..&\sigma_{dd}\\ \end{aligned} \right]\]其中 \(\sigma_{ij} = Cov(X_1, C_2)\)。下面我们将证明 \(Var(Y)\) 的最大值为 \(\Sigma\) 的最大特征值。根据方差的性质
\[Var(Y) =\sum_{i=1}^d\sum_{j=1}^d \omega_i \omega_jCov(X_i,X_j)= \sum_{i=1}^d\sum_{j=1}^d \omega_i \omega_j \sigma_{ij} = \omega^T \Sigma \omega\]容易知道协方差矩阵 \(\Sigma\) 为实对称矩阵，于是它拥有一组可以作为单位正交基的特征向量
\[e_1,e_2...e_d\]满足
\[e_i^T e_j = \left\{ \begin{aligned} 1\quad i = j\\0\quad i \ne j \end{aligned}\right.\]以及相对应的特征值
\[\lambda_1, \lambda_2 ... \lambda_d\]并不失一般性的假设
\[\lambda_1 \ge \lambda_2 \ge ... \ge \lambda_d\]利用这组基向量，我们可以将 \(\omega\) 分解成
\[\omega = \sum_{j=1}^d \alpha_j e_j\]那么
\[Var(Y) = \sum_{i=1}^d \sum_{j=1}^d \alpha_i \alpha_j e_i^T \Sigma e_j = \sum_{i=1}^d \alpha_i^2 \lambda_i \le \lambda_1\sum_{i=1}^n\alpha_i^2\]其中 \(\lambda_1\) 是最大的特征值，上述公式取等号的条件是，与 \(\lambda_1\) 相对应的系数 \(\alpha_1\) 为 1，其他的系数为 0，这时有 \(\omega = e_1\)。再考虑到约束
\[\|\omega\|^2=\sum_{i=1}^d \sum_{j=1}^d \alpha_i \alpha_j e_i e_j = \sum_{i=1}^n \alpha_i^2 =1\]于是可以得出结论
\[Var(Y) \le \lambda_1\]并且当 \(\omega = e_1\) 时，等号成立，对应的映射值就为
\[Y = e_1 \cdot X\]这里的证明就完成了，下面我们换一种思路，采用更直接的方式来计算最大方差，即
\[\max_{\omega} \quad Var(Y)\\ s.t.\quad \|\omega\| = 1\]由于前面的推导，我们已知
\[Var(Y) = \omega^T \Sigma \omega\]于是利用拉格朗日乘子法，建立拉格朗日函数
\[L(\omega, \lambda) = \omega^T \Sigma \omega - \lambda(\omega^T \omega -1)\]对 \(\omega\) 求梯度得到
\[\Delta_{\omega} L = \omega^T \Sigma - \lambda \omega^T\]再令 \(\Delta_{\omega} =0\) ，就有
\[\Sigma \omega = \lambda \omega\]可以看到，\(\lambda\) 就是协方差矩阵的特征值，将上式代入 \(Var(Y)\) ，便得到
\[Var(Y) = \lambda \omega^T \omega = \lambda\]于是我们再一次证明了 \(Var(Y)\) 的最大值就等于协方差矩阵的最大特征值，相对应的 \(\omega\) 就是协方差矩阵的最大特征值对应的特征向量。这里的 \(Y\) 就是对 \(X\) 的一种表征，它只有一个维度，并且与最大的特征值相关，所以称之为 \(X\) 的第一主成分，可用 \(Y_1\) 表示。但是显然，虽然第一主成分能够一定程度上代表原始特征，却失去了原始特征的很多信息，为了尽量补全信息，下面我们将考虑更多的次要成分。
次要成分与数据重建
在我们计算第一主成分的时候，考虑的是用一条直线（在高维情况下为超平面）作为基线，然后将特征点投影上去，用距离作为特征点的代表，并且这条直线使得距离有很好的散布性。同样的道理，计算第二个主成分，也是要找到一条直线或者超平面来做投影，但是它必须要和计算第一主成分时的基线正交，否则得到的第二主成分将有一部分含有第一主成分的信息。于是计算第二主成分的系数向量 \(\omega^{(2)}\) 必须满足条件
\[\omega^{(2)} \cdot e_1 = 0\]以及当然
\[\|\omega^{(2)}\| = 1\]接下来我们将证明，满足上述条件的 \(\omega^{(2)}\) 必然使 \(Y_2 = \omega^{(2)} \cdot X\) 的最大值为 \(\Sigma\) 第二大的特征值 \(\lambda_2\)，并且 \(\omega^{(2)} = e_2\)。首先对 \(\omega^{(2)}\) 进行分解
\[\omega^{(2)} = \sum_{i=1}^d \alpha_i^{(2)} e_i\]考虑到 \(\omega^{(2)}\) 与 \(e_1\) 正交，所以
\[\omega^{(2)} \cdot e_1 = 0\quad \Rightarrow \quad\sum_{i=1}^d \alpha_i^{(2)} e_i \cdot e_1 = 0 \quad \Rightarrow \quad \alpha_1^{(2)} = 0\]也就是说，第一个方向上的分量为 0。然后根据方差的性质
\[\begin{aligned} Var(Y_2) &= \sum_{i=1}^d \sum_{j=1}^d \alpha_i^{(2)} \alpha_j^{(2)} e_i^T \Sigma e_j \\&= \sum_{i=1}^d \sum_{j=1}^d \alpha_i^{(2)} \alpha_j^{(2)} e_i^T \lambda_j e_j\\ &= \sum_{i=1}^d \alpha_i^{(2)} \alpha_i^{(2)} \lambda_i\\ &= \sum_{i=2}^d \alpha_i^{(2)} \alpha_i^{(2)} \lambda_i\\ &\le \lambda_2 \sum_{i=2}^d \alpha_i^{(2)} \alpha_i^{(2)} \end{aligned}\]同样，根据 \(\|\omega^{(2)}\|=1\)，可得
\[\sum_{i=1}^d \alpha_i^{(2)} \alpha_i^{(2)} =1\]于是有
\[Var(Y_2) \le \lambda_2\]其中取等号的条件是，不等式中 \(\alpha_2^{(2)} = 1\)， 其余系数为 0。于是我们就证明了，当 \(\omega_{(2)} = e_2\) 时，\(Var(Y_2)\) 取得最大值 \(\lambda_2\)。
基于同样的方法，我们还能寻找第三主成分，第四主成分等等。将这些主成分 \(Y_1, Y_2, Y_3 ...\) 按列合并，形成新的数据矩阵
\[Y = [Y_1 \quad Y_2 \quad ...\quad Y_m] \quad m \le d\]即为原特征矩阵 \(X\) 的降维变换。
最小重建误差
我们逐步寻找原始数据的第一、第二、第三、第四等等主成分的过程，实际上是在逐步重建数据，比如原始的数据由矩阵 \(X\) 表示
\[X = [X_1 \quad X_2 \quad ...\quad X_d]\]它的每一行表示一个数据点，即
\[x_i = [X_{1i} \quad X_{2i} \quad \cdots \quad X_{di}]\]其中 \(X_{ji}\) 表示 \(X_j\) 的第 i 个分量，而重建之后的数据
\[Y = [Y_1 \quad Y_2 \quad ... Y_m] \quad m \le d\]它的每一行表示一个重建之后的数据点，我们这里用 \(\hat x_i\) 表示
\[\hat x_i = [Y_{1i}\quad Y_{2i} \quad \cdots \quad Y_{mi}]\]其中 \(Y_{ji}\) 表示 \(Y_j\) 的第 i 个分量。
然后我们用主成分分析方法跑一个实际的例子，使用著名的 鸢尾花数据集 。这个数据集包含 3 种鸢尾花的子属，记录了花瓣与花萼的长宽尺寸作为特征。
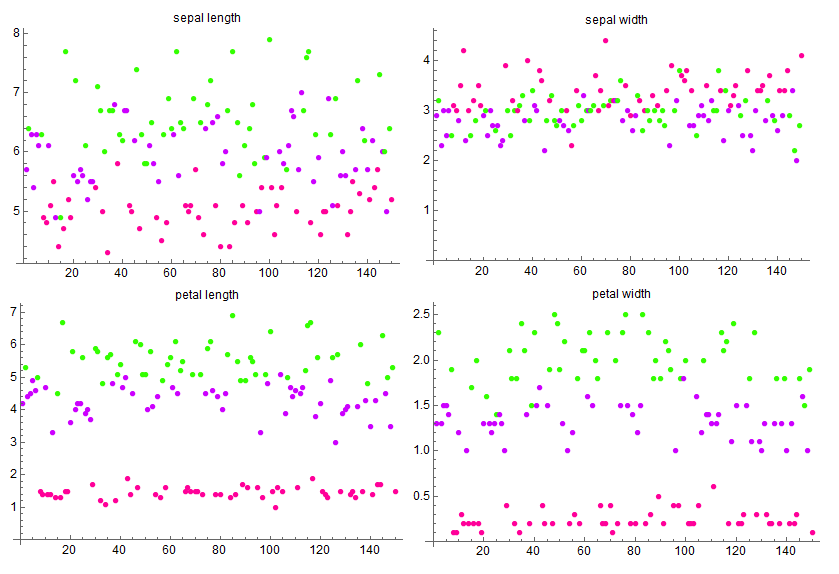（单独使用一种特征绘制的散点图，不同颜色代表不同种类）
分别计算这四个特征的方差值为
\[\begin{aligned} Var(SL) &= 0.685694\\ Var(SW) &= 0.188004\\ Var(PL) &= 3.11318\\ Var(PW) &= 0.582414 \end{aligned}\]这里使用 \(SL, SW, PL,PW\) 分别表示 sepal length, sepal width, petal length, petal width。可以发现，虽然从图上看，petal width 的区分度要明显高于 sepal length，但是它们的方差却是反过来的。细想一下，造成这一现象的原因在于我们没有统一两个特征的度量，这样的话，数值上较大的特征计算的方差肯定会大一点，于是将这些特征归一化处理之后（也就是对每类特征，减去平均值，再除以最大值），再来看看方差
\[\begin{aligned} Var(SL) &= 0.162107\\ Var(SW) &= 0.103771\\ Var(PL) &= 0.315483\\ Var(PW) &= 0.343918 \end{aligned}\]这就要显得合理许多。
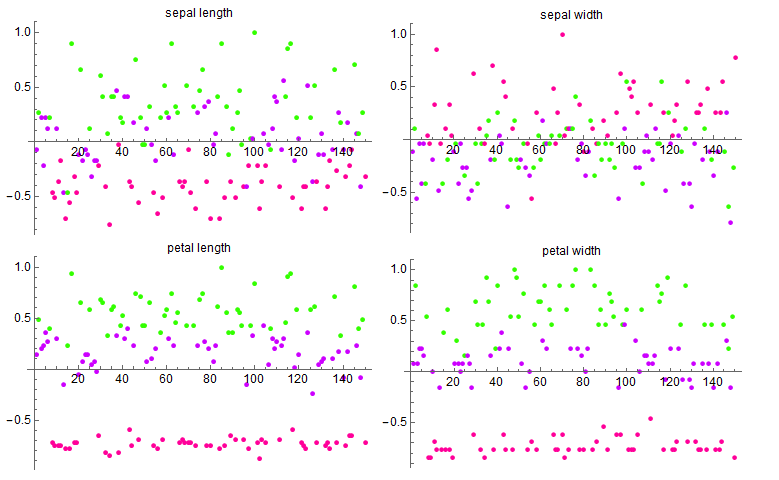（数据归一化之后的特征分布）
然后将归一化的特征代入主成分分析算法，得到的四阶主成分
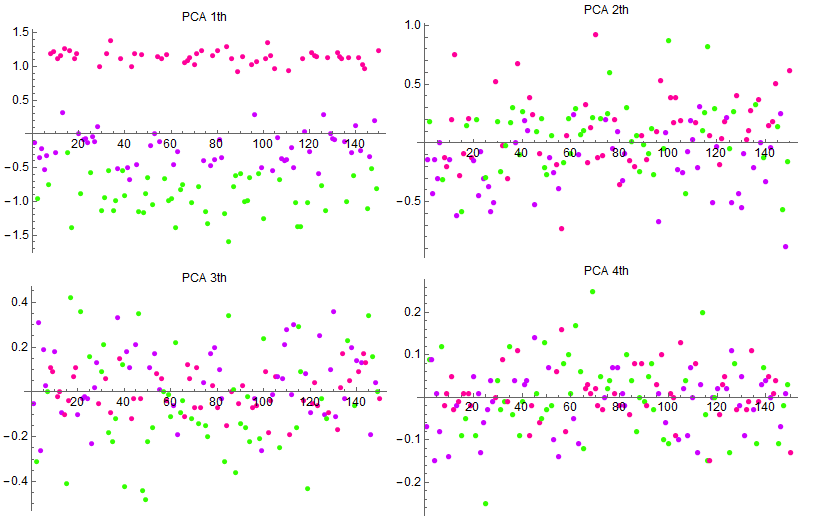
它们的方差（或者说协方差矩阵的特征值）分别为
\[\begin{aligned} Var(Y_1) &= 0.785774\\ Var(Y_2) &= 0.10246\\ Var(Y_3) &= 0.0307906\\ Var(Y_4) &= 0.00600804 \end{aligned}\]可以看到其中第一主成分占据了相当大的一部分，其他成分显得更加次要。通过主成分分析，我们找到了训练特征中最具差异化的特征表达，它或许不具备对应的现实意义，例如花瓣的宽度，只是这些特征的加权组合，却能够更好地表达特征。