Fisher 线性判别分析
设有属于两个类别的 n 个 d 维样本 \(\{x_i\mid \, i \in \{1,2,,n\}\}\),如果它们线性可分,那么一般可以将它们映射到一维空间,并且同样可识别,类似于下图所示的意思
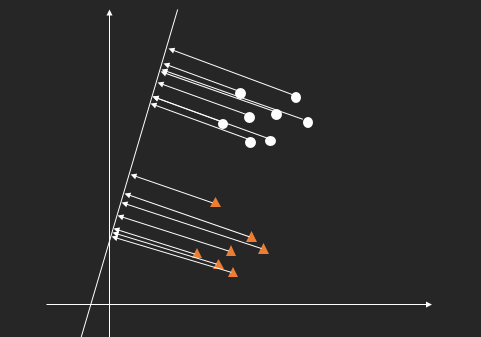
由圆形和三角形标识的两类图形被投影到了直线上,它们的位置是分开的,可以成为判别的依据。所以这就对我们产生了启发,能不能找到这样的直线,使得样本集投影到上面之后能够很轻易地对它们进行分类?
直观的想一下,只要两类样本是可分的,就一定能找得到这样的直线,但是如果像上图这样的投影直线,要识别点在直线上的投影位置,需要一个直线上的参考点,以便计算距离。另一种更方便的方法是投影到另一个方向的直线上
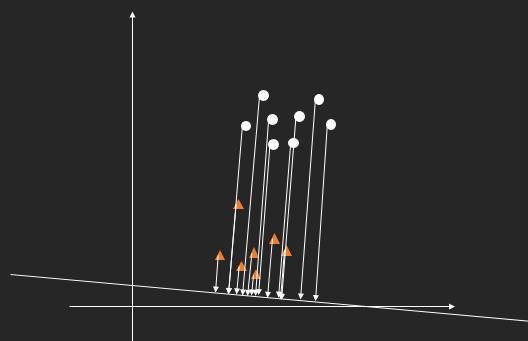
虽然这种方式的投影点没有明显地分开,但是仔细观察会发现样本点到直线的距离是明显分隔成两个级别的。我们假设投影面的方程为
\[\mathbf{w}^T \mathbf{x} + b = 0\]对于空间中的任意点 \(\mathbf{x}\),设其在上述面上的投影点为 \(\mathbf{x}_p\),并且离面的垂直距离为 \(r\)。那么就有关系
\[\mathbf{x} =\mathbf{x}_p + r\frac{\mathbf{w}}{||\mathbf{w}||}\]定义函数
\[y(\mathbf{x}) = \mathbf{w}^T \mathbf{x} +b\]对任意点 \(\mathbf{x}\),代入函数 \(y\) 后可得
\[\begin{aligned} y(\mathbf{x}) &= \mathbf{w}^T (\mathbf{x}_p +r\frac {\mathbf{w}}{||\mathbf{w}||}) + b\\ &= \mathbf{w}^T \mathbf{x}_p + b + r ||\mathbf{w}||\\ &=r ||\mathbf{w}|| \end{aligned}\]对于超平面来说,\(\mathbf{w}\) 的绝对值不起作用,因为可以缩放 \(\mathbf{w}\) 却使平面不发生任何变化,这样的话,如果我们若总是设 \(\|\mathbf{w}\| = 1\),那将更加方便,即
\[y(\mathbf{x}) = r\]也就是说,函数 \(y\) 将空间上的点映射成了它到超平面的垂直距离,通过距离来识别两类数据,这正好符合前面的图所表达的意思。
现在的问题就是如何找到最优的超平面来做投影,我们的需求是使得两类样本的投影距离分开得越大越好,并且同一类样本的投影距离离散的的越少越好。距离的离散度可以用类似于标准差的量来度量
\[S_i^2 = \sum_{\mathbf{x}\in A_i} (y(\mathbf{x}) - \bar{r}_i)^2,\quad i = 1,2\]其中 \(\bar{r}_i =\frac 1 {n_i} \sum_{\mathbf{x}\in A_i} y(\mathbf{x})\\\)
而总的离散度则为
\[S^2 = S_1^2 + S_2^2\]度量两类投影距离的分散量可以考虑为均值差的平方
\[(\bar{r}_1 - \bar{r}_2)^2\]这样一来,我们的优化目标就是选择直线使得 \(S\) 越小越好, \((\bar{r}_1 - \bar{r}_2)^2\) 越大越好。于是可以定义一个总体的目标函数
\[J(\mathbf{w}) = \frac{(\bar{r}_1 - \bar{r}_2)^2}{ S_1^2 + S_2^2}\]这样的函数被称为 Fisher 准则函数,优化目标是找到合适的 \(\mathbf{w}\) 使 \(J(\mathbf{w})\) 取到极大值。
现在分别考虑分子和分母
\[\begin{aligned} \bar{r}_1 - \bar{r}_2 &= \frac 1 {n_1} \sum_{\mathbf{x}\in A_1} y(\mathbf{x}) - \frac 1 {n_2} \sum_{\mathbf{x}\in A_2} y(\mathbf{x})\\ &= \frac 1 {n_1} \sum_{\mathbf{x}\in A_1}(\mathbf{w}^T \mathbf{x} + b) - \frac 1 {n_2} \sum_{\mathbf{x}\in A_2}(\mathbf{w}^T \mathbf{x} + b)\\ &=\mathbf{w}^T \left( \frac 1 {n_1} \sum_{\mathbf{x}\in A_1}\mathbf{x} - \frac 1 {n_2} \sum_{\mathbf{x}\in A_2} \mathbf{x}\right) \end{aligned}\\\]分别定义
\[m_1 = \frac 1{n_1} \sum_{\mathbf{x} \in A_1} \mathbf{x}\\ m_2 = \frac 1{n_2} \sum_{\mathbf{x} \in A_2} \mathbf{x}\]则有化简后的
\[\begin{aligned} (\bar{r}_1 - \bar{r}_2)^2 &= \mathbf{w}^T (m_1 - m_2) (m_1^T - m_2^T)\mathbf{w}\\ &=\mathbf{w}^T S_b \mathbf{w} \end{aligned}\]这里使用 \(S_b = (m_1 - m_2)(m_1^T - m_2^T)\) ,可以通过样本集轻易算出。另外有
\[\begin{aligned} S_1^2 &= \sum_{\mathbf{x} \in A_1} (y(\mathbf{x} ) - \bar{r}_1)^2\\ &= \sum_{\mathbf{x} \in A_1} (\mathbf{w}^T \mathbf{x} + b - \frac 1 {n_1}\sum_{\mathbf{x} \in A_1} (\mathbf{w}^T \mathbf{x} + b))^2\\ &= \sum_{\mathbf{x}\in A_1}(\mathbf{w}^T \mathbf{x} - \frac 1 {n_1} \mathbf{w}^T\sum_{\mathbf{x}\in A_1} \mathbf{x})^2\\ &= \mathbf{w}^T \sum_{\mathbf{x}\in A_1}(\mathbf{x} - \frac 1 {n_1} \sum_{\mathbf{x}\in A_1}\mathbf{x})(\mathbf{x}^T - \frac 1 {n_1} \sum_{\mathbf{x} \in A_1}\mathbf{x}^T) \mathbf{w}\\ &=\mathbf{w}^T \sum_{\mathbf{x} \in A_1} (\mathbf{x} - m_1)(\mathbf{x}^T - m_1^T)\mathbf{w} \end{aligned}\] \[\begin{aligned} S_1^2 +S_2^2 &= \mathbf{w}^T \left( \sum_{\mathbf{x} \in A_1} (\mathbf{x} - m_1)(\mathbf{x}^T - m_1^T) +\sum_{\mathbf{x} \in A_2} (\mathbf{x} - m_2)(\mathbf{x}^T - m_2^T)) \right)\mathbf{w}\\ &= \mathbf{w}^T S_w \mathbf{w} \end{aligned}\]使用 \(S_w\) 代替括号内那一长串公式,同样也能够通过样本集轻松计算。于是 Fisher 准则函数可以写成
\[J(\mathbf{w}) = \frac{\mathbf{w}^T S_b \mathbf{w}} {\mathbf{w}^T S_w \mathbf{w}}\]这是一个广义瑞利商,可以使用拉格朗日乘子法求极值,以及对应的解 \(\mathbf{w}^* {}\)。假定约束 \(\mathbf{w}^T S_w \mathbf{w} = 1\), 定义拉格朗日函数
\[L(\mathbf{w}, \lambda) = \mathbf{w}^T S_b \mathbf{w} - \lambda(\mathbf{w}^T S_w \mathbf{w} - 1)\]求梯度取零
\[\nabla_{\mathbf{w}} L = S_b \mathbf{w} - \lambda S_w \mathbf{w} = 0\]即有
\[S_w^{-1} S_b \mathbf{w}^* = \lambda \mathbf{w}^*\]显然这是一个求解矩阵 \(S_w^{-1} S_b\) 的特征值问题。但是考虑到
\[S_b = (m_1 - m_2) (m_1 - m_2)^T\]于是有
\[\mathbf{w}^* = S_w^{-1} (m_1 - m_2) \frac{(m_1 -m_2)^T \mathbf{w}^* }{\lambda}\]这里的 \(\frac{(m_1 -m_2)^T \mathbf{w}^* }{\lambda}\) 是一个标量,对 \(\mathbf{w}^* {}\) 的方向不起作用,而我们想要确定的实际上是 \(\mathbf{w}^* {}\) 的方向,所以这一项可以忽略而不会造成错误,即
\[\mathbf{w}^* = S_w^{-1} (m_1 - m_2)\]大型矩阵求逆是一项相当复杂的任务,但我们可以通过下面的线性方程组来避免求逆矩阵的困难
\[S_w \mathbf{w}^* = m_1 - m_2\]在前面,为了令 \(y(\mathbf{w}) = r\),我们强制 \(\|\mathbf{w}\| = 1\),于是可以令
\[\mathbf{w}^* = \frac{\mathbf{w}^* } {||\mathbf{w}^* ||}\]至此,我们便找到了投影超平面的方程
\[\mathbf{w}^{* {T}} \mathbf x +b = 0\]这里的 \(b\) 并不是特别重要,因为 \(b\) 的存在只是让直线在坐标系中平移,对特征点到直线的距离有影响,但是如果两类特征到直线的距离能明显区分,那么无论怎样平移直线,这种可区分性都不会有所减损。
将特征点投影到超平面上,单纯地使用投影距离来表示特征点,我们就将高维的数据降到了一维空间,然后再通过决策函数对特征进行分类,这就是 Fisher 线性判别的基本思想。
为了方便起见,这里设 \(b = 0\) ,那么特征点到投影面的距离集合就为
\[\{d_i = \mathbf{w}^{* T} \mathbf{x}_i | \mathbf{x}_i \in A\}\]这样就将原本的训练集合
\[\{(\mathbf{x}_i ,\, y) |\, i \in \{1,2,..,n\},\,\, y \in \{0,1\}\}\]映射到了更简化的训练集
\[\{(d_i ,\, y) |\, i \in \{1,2,..,n\},\,\, y \in \{0,1\}\}\]下面使用一维高斯判别分析对分类模型进行训练
首先假设同一类别的数据服从均值和方差分别为 \(\mu,\, \sigma\) 高斯分布,即
\[p(x) = \frac{1}{\sqrt{2 \pi}\sigma} \exp\left(- \frac{(x-\mu)^2}{2\sigma^2}\right)\]这里的 \(x\) 就是距离 \(d\) , 使用极大似然估计来估计参数可得
\[\begin{aligned} &\mu = \frac 1 n \sum x_i\\ &\sigma^2 = \frac{1}{n} \sum (x_i - \mu)^2 \end{aligned}\]也就是说,对于第 i 类数据
\[\begin{aligned} &\mu_i = \frac 1 {n_i} \sum_{\mathbf{x} \in A_i} d\\ &\sigma_i^2 = \frac{1}{n_i} \sum_{\mathbf{x} \in A_i} (d - \mu)^2 \end{aligned}\]下图可以直观地看出这一建模结果
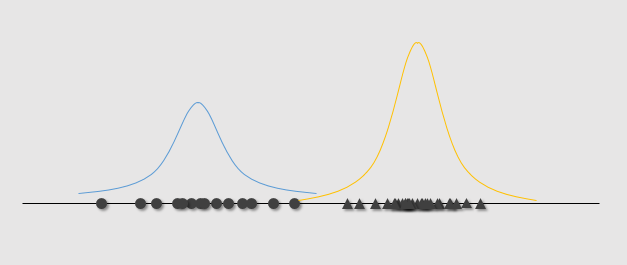
也就是说使用正态分布函数分别对距离集合进行建模,得到概率密度函数
\[p(x|y=0)\sim N(\mu_1, \sigma_1)\\ p(x|y=1)\sim N(\mu_2, \sigma_2)\]预测的时候,将测试数据 \(\mathbf{x}\) 代入公式 \(\mathbf{w}^{* T} \mathbf{x}\) 得到降维数据 \(d\) ,然后将 \(d\) 分别代入上述的两类模型,比较结果大小即可进行判断。
参考资料
模式识别(第二版),边肇祺