感知器
线性分类观点
考虑数据集 \(S = \{x^{(i)}\in R^d\mid i=1,2,,,n\}\) ,其中的样本可以被线性分割成两个类别:\(\mathcal{C}_1, \mathcal{C}_2\) ,然后我们再为每一个 \(x\) 分配一个类别标签值 \(y\),当 \(x^{(i)}\) 属于类别 \(\mathcal{C}_1\) 时,\(y_i=1\) ,否则 \(y_i=-1\) 。定义分割超平面为
\[\omega^T x + b = 0\]其中 \(\omega, x\) 都是 d 维向量。然后对任意的 \(x \in S\) ,定义函数
\[r(x) = \frac{\omega^T}{\|\omega\|} x+ \frac b{\|\omega\|}\]容易证明 \(r(x)\) 的模实际上就是点 \(x\) 到超平面的距离,至于 \(x\) 在超平面的哪一侧,则由 \(r(x)\) 的符号决定。并且规定,使 \(r(x) > 0\) 的类别,标签值 \(y=1\),否则 \(y=-1\) 。于是我们看到,如果点 \(x^{(i)}\) 被超平面错误分类,例如 \(x^{(i)}\) 的类别标签 \(y_i = 1\) ,但是 \(r(x^{(i)})\) 却小于 0,则有
\[y_i r(x^{(i)}) < 0\]然后定义目标函数
\[J(\omega, b) = -\sum_{x^{(i)} \in \mathcal{E}} y_i r(x^{(i)})\]其中 \(\mathcal{E}\) 表示被超平面错分的数据集合。这表达的是所有错分数据到超平面的距离和,显然,被错误分类的数据越少, \(J(\omega,b)\) 的值也越小,并且当所有点都被正确分类时极值为 0。所以我们的优化目标就是
\[\min_{\omega ,b} \quad J(\omega, b)\]下面我们尝试采用梯度下降法来求解该优化问题,首先计算 \(J(\omega, b)\) 关于 \(\omega\) 的梯度,两端同时乘以 \(\|\omega\|\)
\[J(\omega, b) = -\sum_{x^{(i)}\in \mathcal{E}} y_i \left(\frac {\omega^T}{\|\omega\|}x^{(i)} + \frac b {\|\omega\|}\right)\\ \Rightarrow \|\omega\|J(\omega, b) = -\sum_{x^{(i)}\in \mathcal{E}} y_i (\omega^T x^{(i)} + b)\]其中 \(\|\omega\|=\sqrt{\omega^T \omega}\) ,然后两端关于 \(\omega\) 求梯度
\[\begin{aligned} &\nabla_{\omega}(\sqrt{\omega^T \omega}) J + \sqrt{\omega^T \omega}\nabla_{\omega} J = -\sum_{x^{(i)}\in \mathcal{E}}y_i x^{(i)}\\ \Rightarrow& J\frac{\omega}{\|\omega\|}+ \|\omega\| \nabla_{\omega} J = -\sum_{x^{(i)}\in \mathcal{E}}y_i x^{(i)}\\ \Rightarrow&\nabla_{\omega} J = \frac 1 {\|\omega\|^2}\left(-\|\omega\|\sum_{x^{(i)}\in \mathcal{E}}y_i x^{(i)} -J \omega \right)\\ &= \frac 1 {\|\omega\|^2}\left(-\|\omega\|\sum_{x^{(i)}\in \mathcal{E}}y_i x^{(i)} + \sum_{x^{(i)}\in \mathcal{E}} y_i \left(\frac {\omega^T\omega} {\|\omega\|}x^{(i)} + \frac {b \omega} {\|\omega\|}\right) \right)\\ &=\frac {b\omega} {\|\omega\|^3}\sum_{x^{(i)}\in \mathcal{E}}y_i \end{aligned}\]所以 \(\omega\) 的更新过程分别为
\[\omega^{(k+1)} = \omega^{(k)} -\alpha \frac {b^{(k)}\omega^{(k)}} {\|\omega^{(k)}\|^3}\sum_{x^{(i)}\in \mathcal{E}}y_i\]但是上式右端每一项都含有 \(\omega\) ,这就意味着如果 \(\omega\) 的某个分量为 0,那么更新的过程中就一直都为 0,显然这个问题并不适合采用梯度下降法。
现在我们重新审视一下这个问题,为了获得分类超平面,我们将损失函数定义成了错分数据到试探超平面的绝对距离之和,但最后发现这样定义的问题无法用梯度下降法求解。于是我们放弃使用绝对距离转而使用相对距离,即
\[\hat{r}(x) = \omega^T x + b\]该值与 \(r(x)\) 的符号是一样的,只不过少了一个放缩系数 \(\|\omega\|\) ,现在让我们使用错分点距超平面的相对距离之和来作为损失函数
\[J(\omega, b) = -\sum_{x^{(i)} \in \mathcal{E}} y_i (\omega^T x^{(i)}+b)\]同样地,该函数在不存在错分点的情况下,到达极值 0 ,并且在相等的 \(\omega\) 情况下,错分点越少,值也越小。它对 \(\omega\) 的梯度为
\[\nabla_\omega J = - \sum_{x^{(i)} \in \mathcal{E}} y_i x^{(i)}\]如果定义向量 \(\mathbf{w} = [b\quad \omega]\) ,并且再对每个数据增加一个维度,将其设值为 1,即 \(\mathbf{x} = [1\quad x]\),那么超平面方程就可以写成更紧凑的形式
\[\mathbf{w}^T \mathbf{x} = 0\]而且,优化目标也变成了
\[\min_{\mathbf{w}}\quad J(\mathbf{w})\]使用梯度下降法,可以求取这个优化问题的解,迭代格式如下
\[\mathbf{w}^{(k+1)} = \mathbf{w}^{(k)} + \alpha \nabla_{\mathbf{w}} J(\mathbf{w^{(k)}})\]其中
\[\nabla_{\mathbf{w}} J(\mathbf{w}) = -\sum_{\mathbf{x}^{(i)} \in \mathcal{E}} y_i \mathbf{x}^{(i)}\]一个简单的实现
首先我们生成一些训练数据,所有点在 \([0,0],[100,0],[100,50],[0,50]\) 围成的矩形之中,然后使用直线 \(x+2y=100\) 把所有点分成两类,代码如下
//定义直线方程
Function<double[], Double> strightLine = x -> 100 - x[0] - 2*x[1];
//随机数生成器
Random random = new Random();
random.setSeed(123);
//这里将类别标签值放在每个数组的第三个索引位置
List<double[]> data = IntStream.rangeClosed(1, 100).boxed()
.map(i -> new double[]{random.nextDouble() * 100, random.nextDouble() * 50})
.map(p -> new double[]{p[0], p[1], strightLine.apply(p) > 0 ? 1 : -1})
.collect(Collectors.toList());
结果如下图
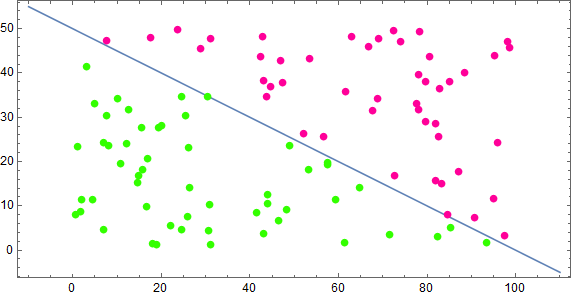
接下来初始化一些参数
//直线系数数组
final double[] w = {1, 1, 1};
//系数数组,用于存储每次更新后的值
final double[] w2 = new double[3];
//学习速率
final double alpha = 0.01;
//判断直线是否将点 x 正确分类
Function<double[], Boolean> isRight = x -> x[3] * (w[0] + w[1] * x[0] + w[2] * x[1]) > 0;
//判断梯度下降是否收敛,这里使用两次更新差的模作为衡量标准,阈值设为 0.01
final double epsilon = 0.01;
BiFunction<double[], double[], Boolean> isConverge = (before, after) -> {
double[] sub = {after[0] - before[0], after[1] - before[1], after[2] - before[2]};
return Math.sqrt(sub[0] * sub[0] + sub[1] * sub[1] + sub[2] * sub[2]) < epsilon;
};
最后使用梯度下降法进行计算
do{
w2[0] = w[0];
w2[1] = w[1];
w2[2] = w[2];
double[] delta = data.stream()
.filter(isRight::apply)
.map(x -> new double[]{x[2] * 1, x[2] * x[0], x[2] * x[1]})
.reduce(new double[]{0, 0, 0}, (d1, d2) -> new double[]{d1[0] + d2[0], d1[1] + d2[1], d1[2] + d2[2]});
w[0] -= alpha * delta[0];
w[1] -= alpha * delta[1];
w[2] -= alpha * delta[2];
}while(!isConverge.apply(w, w2));
总共迭代次数 4358 次,最终结果
\[\mathbf{w} = [-622.05\quad 6.20\quad12.23]\]中间过程如下图
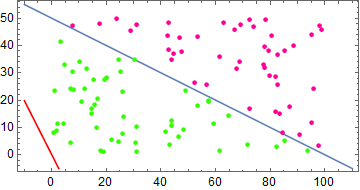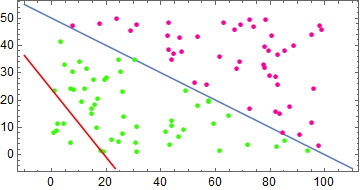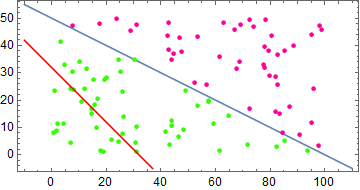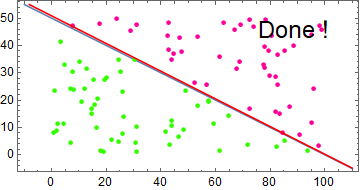
单层感知器
上面描述分类平面就被称为感知器,当然是最简单的二分类单层感知器,它是神经网络的基础单元。上面对感知器的描述是站在线性分类器的角度,如果用神经元的形式来描述,它的分类过程可以用下图表示
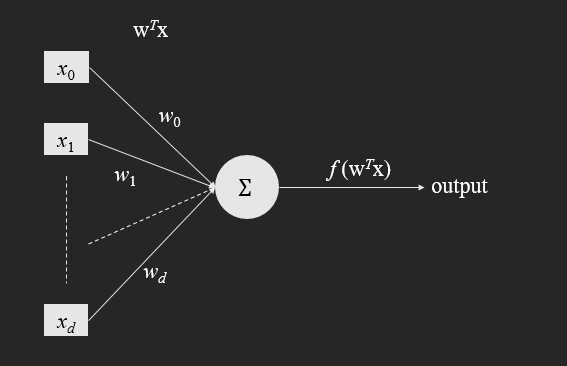
其中 \(x_0 = 1, w_0 = b\) 。这里的 \(x_i,\, i =0,1,,,d\) 是数据 \(\mathbf{x}\) 的分量,\(w_i,\, i =0,1,,,d\) 是 \(\mathbf{w}\) 的分量。并且可以发现,和前面超平面分类的解释相比,这里的 \(w_i\) 更像是特征 \(x_i\) 的权重系数,它由前面所述的梯度下降法计算。
对于任意的待分类数据,如果用超平面的观点,那就是通过计算 \(r(x) = \mathbf{w}^T\mathbf{x}\) ,观察它的正负,确定该点位于超平面的哪一侧,从而进行判断。把这一过程映射到感知器中,则是按权重计算 \(\mathbf{x}\) 各分量之和,然后通过激活函数 \(f(x)\) 的输出进行判断,其中 \(f(x)\) 如下
\[f(x) = \left\{\begin{aligned} & -1\quad x < 0\\ &1 \quad \quad x > 0 \end{aligned} \right.\]与支持向量机相比,感知器貌似只满足于将所有数据正确分类,而不像支持向量机那样,尽可能最大化分类间隔。所以单就这一角度来看,支持向量机应该是优于感知器的,但是随着多层感知器以及神经网络的发展,支持向量机也不再如以前那样繁荣了。