算法题：零钱兑换

问题描述与分析

感觉是一道经典的算法题，笔试面试屡试不爽。如果想把一些钱换成零钱，请问有多少兑换种方法？当然可以具体点，比如有 w 元钱，想用 k 种面额的币来兑换（k种面额可以不全部用完）。如果没有掌握一定的技巧，拿到这题是一脸蒙蔽的。首先我们需要将问题表述数学化一点：

设共有 k 种面额的纸币，分别值 \(v_i, (i = 1,,k)\)，需要兑换的钱为 w ，求总的兑换方法数量 \(N_{k,w}\)。

这道题的关键是将 \(N_{k,w}\) 拆分成两个部分：

一部分是使用 \(k-1\) 种纸币兑换 \(w\) 元钱的方法数量 \(N_{k-1,w}\)
另一部分用 \(k\) 种纸币兑换成 \(w-v_k\) 这么多钱的方法数量 \(N_{k, w-v_k}\)，之所以减去 \(v_k\) 是为了留一个空缺，用 \(v_k\) 来填充，保证此方法至少可以包含一张 \(v_k\) 面额的。

所以第一部分表示完全不使用 \(v_k\) 这种纸币的兑换方案数量，而第二部分表示一定使用了 \(v_k\) 的数量，两者之和就是总的兑换方法数量，因此就可以得出拆分结构

\[N_{k, w} = N_{k,w-v_k} + N_{k-1, w}\]

依照上述方式，\(N_{k,w - v_k}\) 又可拆分成

\[N_{k, w-v_k} = N_{k, w-v_{k}-v_{k-1}} + N_{k-1, w - v_k}\]

同理

\[N_{k-1,w} = N_{k-1,w-v_k} + N_{k-2,w}\]

依次类推，通过上述递归最终将得到该问题的极端情况之一，即：使用 1 元的纸币来兑换 1 元钱，方法数量为 \(N_{1,1}=1\) 。但 \(N_{1,1}\) 仍可以拆分成两个子问题，分别是

使用 0 种纸币来兑换 1 元钱，数量为 \(N_{0,1}\)
使用 1 元纸币来兑换 0 元钱，数量为 \(N_{1,0}\)

于是有

\[N_{1,1} = N_{0,1} +N_{1,0} = 1\]

那么 \(N_{1,0}\) 和 \(N_{0,1}\) 必然有一个等于 0，另一个等于 1。究竟哪一个等于 1？我们可以这样考虑：前面在拆分 \(N_{k,w}\) 的时候，我们把 不使用纸币 \(v_1\) 作为了一种情况大类，那么现在，我们也可以把 不使用 1 元纸币 作为一种兑换方式，所以说有 \(N_{1,0} = 1\)。至于为什么 \(N_{0,1}\) 就得等于 0 呢？这是因为这种情况下已经没有可用的纸币了，我们没有使用或不使用的选择权力。

依据上述考虑，我们也可以类推到

当纸币数量不止一种，但是可兑换金额却等于 0 的时候，兑换方式也只有 1 种，那就是不使用任何纸币，即 \(N_{x, 0} = 1,1\le x\le k\) 。
而当可兑换金额小于零时，则不存在任何兑换方式，即 \(N_{x,y} = 0, y <0\) 。
并且当无纸币可用时，也不存在任何兑换方式，即 \(N_{0,y}=0\) 。

这就是三种退化情况，我们将使用这些条件来终止递归。

代码实现

//version 0.1
public class CoinChange {
    //纸币面额数组
    private int[] v;

    public CoinChange(int[] v) {
        this.v = v;
    }

    public int countingChange(int w){
        return countingChange(v.length, w);
    }

    private int countingChange(int k, int w) {
       if(k <= 0 || w < 0) {
           return 0;
       }
       if(w == 0) {
           return 1;
       }
       return countingChange(k - 1, w) + countingChange(k,w - v[k-1]);
   }

    public static void main(String[] args) {
        int[] v = {1, 2, 5, 10, 20, 50};
        int W = 100;

        int count = new CoinChange(v).countingChange(W);
        System.out.println(count);
    }
}

重构 1

虽然上述的实现确实能解决问题，但是不难发现，递归过程有太多冗余计算，以 w = 6 为例，下图展示了方法 countignChange(int index, int w) 的树形递归计算过程（为了简化，这里采用 cc 代指该方法名）

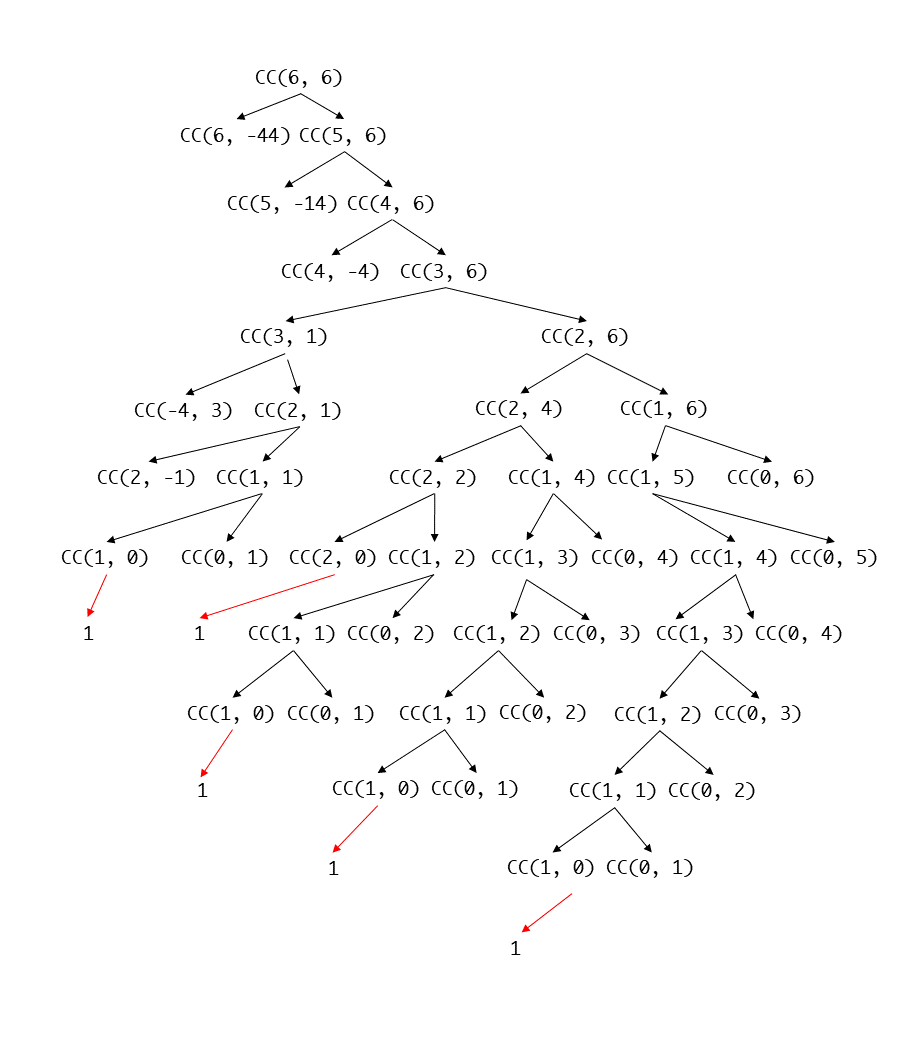
下面我们想办法把中间的计算结果缓存起来，对于重复计算直接查询即可。代码如下

//version 0.2
public class CoinChange {

    private int[] v;

    public CoinChange(int[] v) {
        this.v = v;
    }

    public int countingChange(int w) {
        //申明中间过程缓存数组，并将所有值置为 -1，以便检查是否已有缓存值
        int[][] cache = new int[v.length][w + 1];
        for (int i = 0; i < cache.length; i++) {
            Arrays.fill(cache[i], -1);
        }
        return countingChange(v.length, w, cache);
    }
    private int countingChange(int index, int w, int[][] cache) {
        if(k <= 0 || w < 0) {
            return 0;
        }
        if(w == 0) {
            return 1;
        }
        int c1, c2;
        //如果发现要计算的值已被缓存，那么直接读取即可，否则进行计算，并且将结果缓存到 cache 数组
        if(cache[k-1][w] != -1) {
            c1 = cache[k-1][w];
        }else{
            c1 = countingChange(k - 1, w, cache);
            cache[k - 1][w] = c1;
        }
        if(w - v[k-1] >= 0 && cache[k][w - v[k-1]] != -1) {
            c2 = cache[k][w - v[k-1]];
        }else{
            c2 = countingChange(k,w - v[k-1], cache);
            if(w - v[k-1] >= 0) {
                cache[k][w - v[k-1]] = c2;
            }
        }
        cache[k][w] = c1 + c2;
        return c1 + c2;
    }

    public static void main(String[] args) {
        int[] v = {1, 2, 5, 10, 20, 50};
        int W = 100;

        int count = new CoinChange(v).countingChange(W);
        System.out.println(count);
    }
}

使用较大的 w 可以发现重构后的代码比之前要快无数倍。但这本质上仍然是递归过程，当调用栈过大时会抛出 StackOverflow 错误。比如，设置虚拟机参数 -Xss180k，当 w = 10000 时，在我的机器上最大栈深度到达 2134 就出错了，所以接下来我们考虑使用纯的迭代过程实现。

重构 2

如果说递归是化整为零的方法，那么使用迭代修改的递归算法则是一种从底层逐步累积的哲学。还是借助于 cache 数组来逐步构建 \(k\) 和 \(w\) 增长时的解，并且 cache[i][j] 表示的是当纸币种类为 i，总金额为 j 时的解。构建过程其实就是利用递归式自底向上计算，如果用 cache 符号来改写递归式的话，就得到

cache[k][w] = cache[k][w - v[k-1]] + cache[k-1][w];

而根据退化条件，可知 cache[0][y] = 0, cache[x][0]=1,cache[0][0]，这就是 cache 的初始化值。

重构代码如下

//version 0.3
public class CoinChange {

    private int[] v;
    public CoinChange(int[] v) {
        this.v = v;
    }

    public int countingChange(int w) {
        int[][] cache = new int[v.length + 1][w + 1];
        //初始化 cache
        for (int i = 1; i < cache.length; i++) {
            cache[i][0] = 1;
        }
        for (int i = 0; i < cache[0].length; i++) {
            cache[0][i] = 0;
        }

        for (int i = 1; i < v.length + 1; i++) {
            for (int j = 1; j < w + 1; j++) {
                int index = j - v[i - 1];
                int temp;
                if(index < 0) {
                    temp = 0;
                }else {
                    temp = cache[i][index];
                }
                cache[i][j] = temp + cache[i - 1][j];
            }
        }
        return cache[v.length][w];
    }

    public static void main(String[] args) {
        int[] v = {1, 2, 5, 10, 20, 50};
        int W = 100;

        int count = new CoinChange(v).countingChange(W);
        System.out.println(count);
    }

双重循环里面最重要的逻辑是对递归式的实现，即

cache[i][j] = temp + cache[i - 1][j];

这里使用了一个临时变量 temp 来代替递归式中的 cache[i][j - v[i-1]]，其原因在于索引 j - v[i-1] 有可能为负值，如果为负，就意味着金额小于 0 了，那么自然兑换方式只有 0 种，于是在编程中使用了 temp 变量来实现这一细节。

使用迭代方式避免了深度递归调用，此时再令 w = 10000，就不会出现 StackOverflow 错误了，当然如果无限制地增加 w，会使结果超出 Java 规定的整数上界，那就是另一回事了。