Delaunay 网格划分算法
将一块区域进行网格化是计算几何中的一项重要议题,基于化繁为简的思想,任何复杂的模型都能分解成简单的几何元素。在应用上,整体的非线性行为,便可以由局部的线性拼接得到。
举个简单的例子,一段向上的楼梯,老远看去就是一条斜向上的直线,但实际上是由一段段水平和竖直的线段连成的。从某种意义上讲,将斜线表述成水平线和竖直线的组合降低了描述的层次,但代价是我们需要维护大量的低层次信息。或许对于一段斜直线来讲,这种代价并不值得,但对于更高层次的复杂信息,局部简化是我们目前唯一的办法。
定义
Delaunay 网格划分不是一种具体的算法,而是一种规范,它确保了网格中的三角形的形状处于可控的状态。这是网格划分中不得不考虑的问题,如果同一个单元中的节点离得老远,那么在插值的时候,其误差便没有保证,因为我们知道插值算法的精度依赖于距离。
考虑网格中相邻边的两个三角形
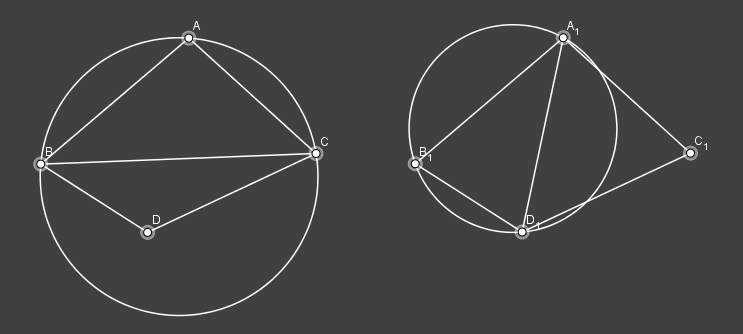
按左边连接方式,会发现 D 点位于三角形 ABC 的外接圆内,而如果换成右边的连接,则 C 点位于 ABD 的外接圆之外,可以证明右边的三角形最小内角大于左边,也意味着右边的三角剖分优于左边。这是一种普遍的情况,于是可以将 BC 边标记为非法边,在网格划分算法中遇到这种情况就需要对其进行翻转,即删除 BC、连接 AD、删除 ABC,BDC、生成 ABD,ACD 。
平面点集的网格划分
首先考虑一种比较简单的需求,已知平面上的一组点,现在要将其连接成网格,并满足 Delaunay 条件。随机增量算法将是一种很好的方式,思想是假设使用前 n 个点已经形成了满足条件的网格,然后插入第 n + 1 个点,增量执行这一过程,直到所有点都加入到网格中,则完成了这堆点的网格划分。现在来看看将第 n + 1 个点插入网格需要完成的操作
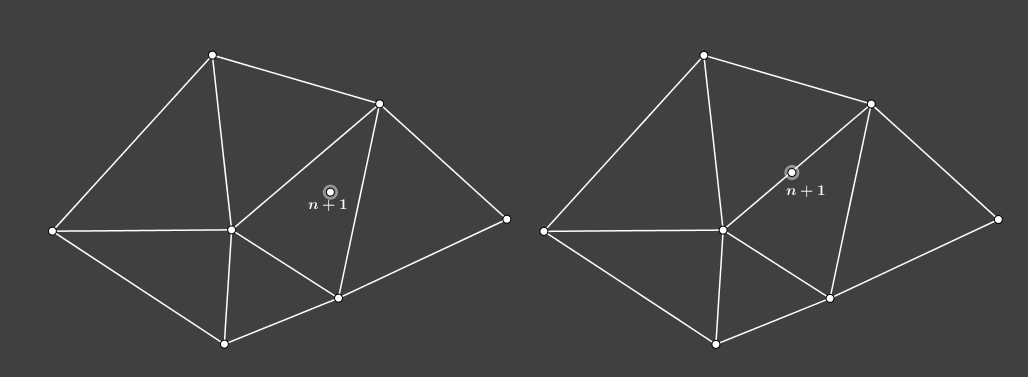
这里存在两种情况,位于三角形内部,或者位于三角形边上。在第一种情况下,首先找到此点所在的三角形,然后分别连接 n+1 与三角形的三个端点,这样就将新点插入到了网格中,但是很显然,除了还没检查的新生成边,原本合法的边也变成了潜在的非法边。
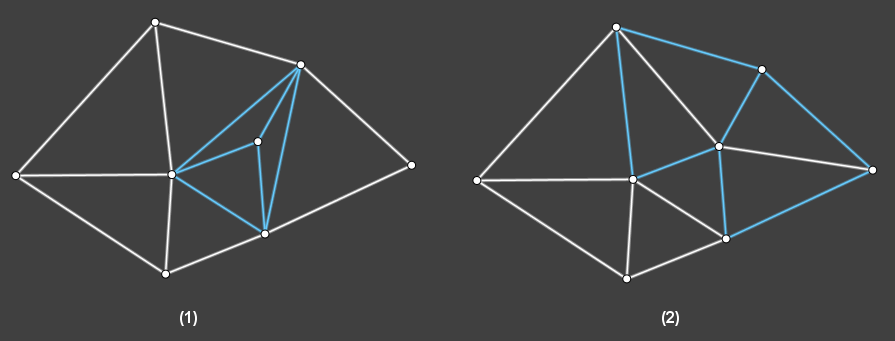
上图左边显示了插入一个点后,需要检查的边的情况,首先对原三角形的边进行检查并翻转非法边,得到右边的图形,由于翻转操作生成了新的三角形,又需要标记检查新的潜在非法边,持续这一过程直到所有边都合法为止。
关于初始化
前面描述了增量过程,但是在最开始我们并没有一个现成的 Delaunay 网格。一种简单的方式是用一个足够大的初始三角形将所有点包含进来,然后使用增量方式插点,完成之后再删除外围的点和线段。
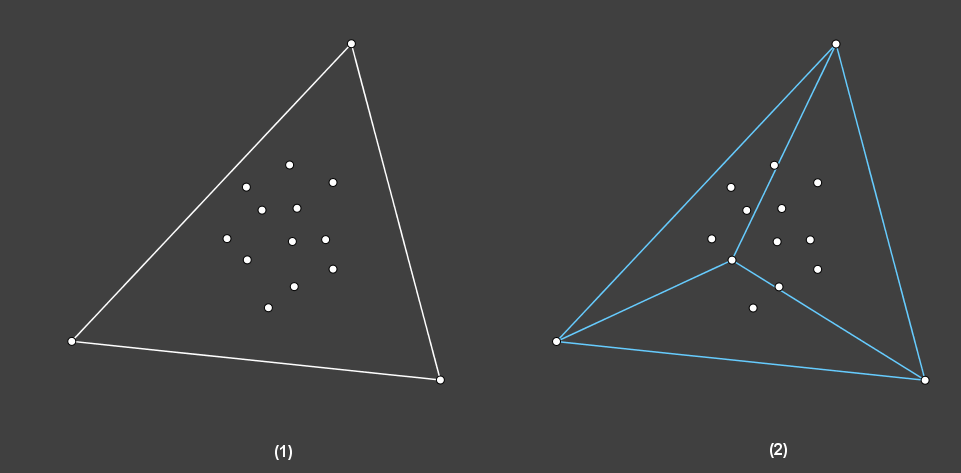
建议的初始外围三角形为 A(-4m, -4m), B(4m, 0), C(0, 4m),其中 m 为所有点中绝对值最大的坐标值。
数据结构
在插入点的过程中,要进行非常多的查询操作,例如查询给定点所在的三角形编号、一条边所在的一个或两个三角形编号等等,因此有必要维护一个高效的数据结构来支持这些查询。
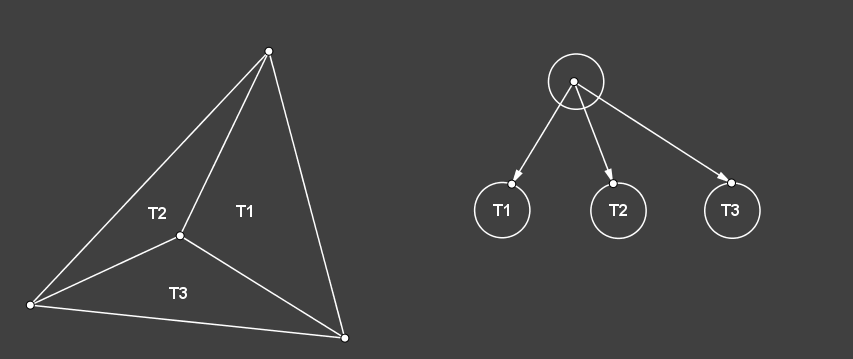
对于三角形集合,我们使用一个有向无环图来表示所有的剖分历史,以最初的外围三角形为根节点,第一次剖分引入三个小三角形,对应于从根节点指向三个子节点
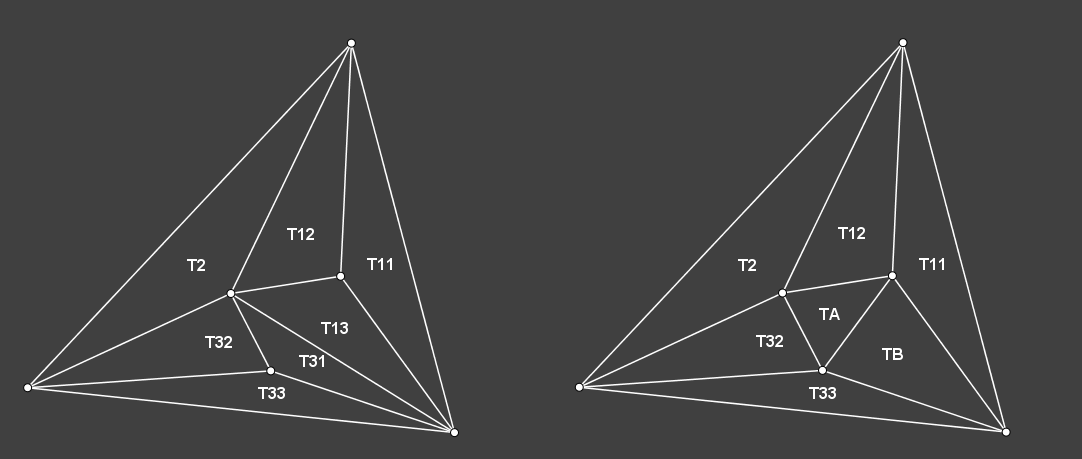
而如下图的一次翻转操作则对应用于将涉及的两个节点 T31 和 T13 指向新节点 TA 和 TB
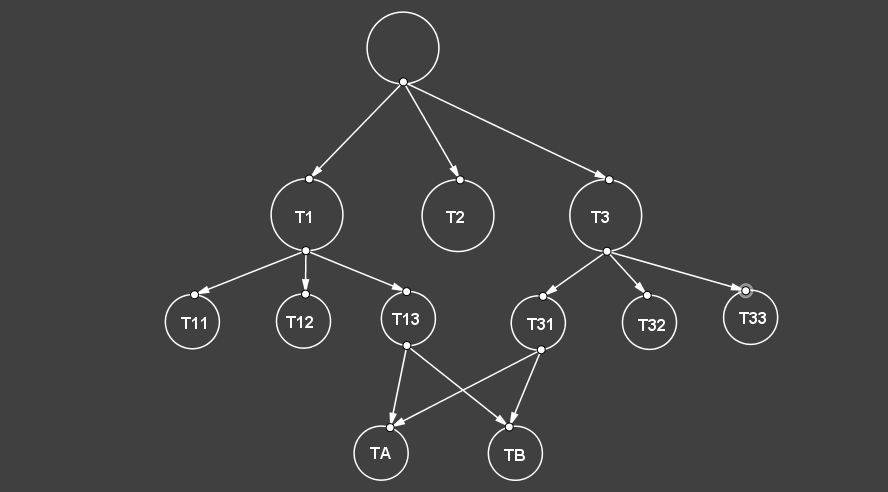
使用这种结构,若要查询给定点所在的三角形,则从根节点开始,依次计算三个子节点,找到那个包含查询点的三角形,然后再计算它的子节点,以此类推,最终到达的叶节点即为要查询三角形。
另一方面,为了对三角形进行快速查询,我们使用数组来存储网格单元,其中每一行是三角形顶点编号,并且所有顶点也用数组来存储。
triangles:
| Index | v1 | v2 | v3 | flag |
|---|---|---|---|---|
| 0 | 0 | 1 | 2 | |
| 1 | 1 | 2 | 3 | |
| 2 | 1 | 2 | 4 | |
| … | … | … | … |
vertices:
| Index | x | y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 10 | 0 |
| 2 | 0 | 10 |
| … | … | … |
前面所说的有向无环结构存储的实际上是三角形的索引号。由于查询点的过程依赖于网格剖分历史,所以在删除单元的时候不能直接将其从数组中移除,而应该使用标记删除的方法,上面 triangles 数组中的标志 flag 位即用于此目的。
在插入点生成新的单元之后,需要检查旧单元的边是否合法,这就需要使用两个点的索引号来查询边,并找到邻边的三角形。这里仍使用数组来存储边的信息,但为了高效的通过顶点查询,我们使用搜索二叉树来存储边的索引号,搜索方式为边的中点坐标,从左到右,从下到上。
同时,边的信息应该包含其所在的一个或两个三角形,以及一个删除标志位(因为二叉树存储了边的索引号,不能直接将边从数组中移除)。
edges:
| Index | v1 | v2 | t1 | t2 | flag |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 2 | 1 | 2 | |
| 2 | 2 | 3 | 3 | 3 | |
| … | … | … | … | … | … |
非法边检测
假设相邻的两个三角形为 ABC 和 BCD ,四个点的坐标分别为
\[A(a_x, a_y),\quad B(b_x, b_y),\quad C(c_x, c_y),\quad D(d_x, d_y)\]那么可以计算得到三角形 ABC 的外接圆心坐标为
\[x = (c_1 * a_2 - c_2 * a_1) / (a_2 * b_1 - a_1 * b_2)\\ y = (c_1 * b_2 - c_2 * b_1) / (a_1 * b_2 - a_2 * b_1)\]其中
\[\begin{aligned} a_1 &= b_x - a_x\\ b_1 &= b_y - a_y\\ c_1 &= \frac 1 2 (b_x^2 - a_x^2 + b_y^2 - a_y^2)\\ a_2 &= c_x - b_x\\ b_2 &= c_y - b_y\\ c_1 &= \frac 1 2 (c_x^2 - b_x^2 + c_y^2 - b_y^2) \end{aligned}\]然后再计算 D 点与圆心的距离是否大于外接圆半径就可以判断了。
待续