共轭梯度法解线性方程组
之前提到,求解线性方程组 \(A x = b\) 等价于求下面二次型的极小值
\[f(x) = \frac 1 2 x^T A x - x^T b\]在最速下降算法中,迭代点沿负梯度方向移动,这就导致迭代点走位太罗嗦,具体来说,若函数的等高线是很狭窄的椭圆,如果初始点取得不好,那么将会产生如下图所示低效的迭代路径

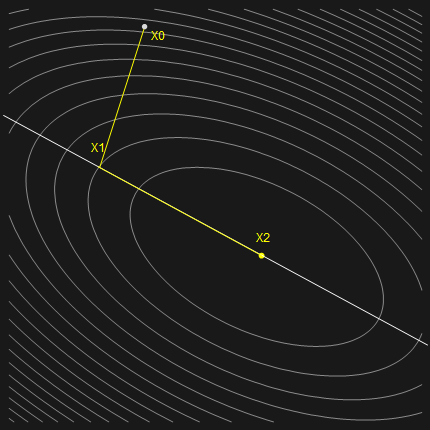
仅仅是二阶矩阵就需要如此多的迭代显然是不可接受的,那么是否有使用极少迭代次数便成功收敛的算法呢?答案是显然的,在上一节讨论最速下降算法的时候,我们谈到了一种特殊情况,即迭代点刚好落在椭圆的轴上,便只用执行一次迭代。所以现在的想法是能不能将初始点经过一次迭代就移动到椭圆的轴上,类似于下图
虽说这是很理想的方案,但此时迭代步长和方向都是未知的,我们可以先分别假设为 \(\alpha^{(k)}, d^{(k)}\),然后考虑迭代格式
\[x^{(k+1)} = x^{(k)} + \alpha^{(k)} d^{(k)}\]为了使得 \(f(x^{(k+1)})\) 关于 \(\alpha^{(k)}\) 取得极小值,需要
\[\begin{aligned} \frac{\mathrm{d}f(x^{(k+1)})} {\mathrm{d}\alpha^{(k)}} &= 0\\ \frac{\mathrm{d}f(x^{(k+1)})} {\mathrm{d}x^{(k+1)}} \frac{\mathrm{d}x^{(k+1)}} {\mathrm{d}\alpha^{(k)}}&=0\\ -r^{(k + 1)} \cdot d^{(k)} &= 0\\ A e^{(k+1)}\cdot d^{(k)} &= 0\\ A (e^{(k)} + \alpha^{(k)} d^{(k)}) \cdot d^{(k)} &= 0\\ \alpha^{(k)} &= \frac{-A e^{(k)} \cdot d^{(k)}}{A d^{(k)}\cdot d^{(k)}}\\ \alpha^{(k)} &= \frac{r^{(k)} \cdot d^{(k)}}{A d^{(k)}\cdot d^{(k)}} \end{aligned}\]如果等高线是同心圆呢?
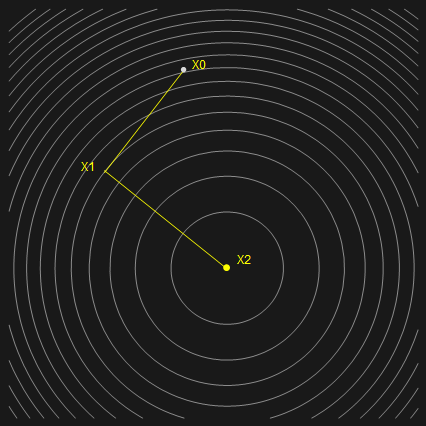
上图看似多此一举(因为前面说到这种情况只需一步迭代),其实是为了和椭圆情况兼容,才能继续下面的讨论。
我们知道圆压扁了就成了椭圆,那如果把上图压扁,迭代路线会产生怎样的变化?可以想象,不一定能得到和前面椭圆图一样的路径,但这就给我们以启发,就是总能找到合适的路线使得算法两步收敛,而不必拘泥于第一步要步进到椭圆轴上。
具体来讲,在二阶情况下,假设等高线是圆,那么总能通过两条垂直的线段连接初始点和圆心。三阶矩阵时,假设等高线是球,这时需要三条,以此类推,n维球需要n条线段,并且这 n 条线互为正交。
对于更一般的椭圆或者超椭球形等高线,我们可以想象先将其拉伸成圆形或者超球,然后确定迭代路线,用向量 \(\mathbf{d}^{(i)}, i = 0,1,,,n-1\) 表示(显然这组向量正交)。之后再恢复原来的形状,此时迭代路线肯定变得不再正交了,用向量组 \(\mathbf{\bar{d}}^{(i)}, i = 0,1,,,n-1\) 表示,但可以证明这组向量满足 A-正交关系,即
\[A \mathbf{\bar d}^{(i)} \cdot \mathbf{\bar d}^{(j)} = 0 \quad i \neq j\]由于变换前 \(\mathbf{d}^{(i)}, i = 0,1,,,n-1\) 正交,所以变换后 \(\mathbf{\bar d}^{(i)}, i = 0,1,,,n-1\) 仍张成整个空间。假设初始误差为 \(e^{(0)}\),那么可将其表示为
\[e^{(0)} = \sum \delta_i d^{(i)}\]为了求得系数 \(\delta_i\),使用 \(A d^{(j)}\) 点积两边
\[\begin{aligned} A d^{(j)} \cdot e^{(0)} &= \sum \delta_i A d^{(j)} \cdot d^{(i)}\\ A d^{(j)} \cdot e^{(0)} &= \delta_j A d^{(j)} \cdot d^{(j)} \\ \delta_i &= \frac{A d^{(j)} \cdot e^{(0)}}{\delta_j A d^{(j)} \cdot d^{(j)}}\\ \delta_i &= \frac{A d^{(j)} \cdot (e^{(0)} + \sum_i^{j-1}\alpha^{(i)} d^{(i)})}{\delta_j A d^{(j)} \cdot d^{(j)}}\\ \delta_i &= \frac{A d^{(j)} \cdot e^{(j)}}{\delta_j A d^{(j)} \cdot d^{(j)}}\\ \delta_i &= \frac{-r^{(j)}\cdot d^{(j)}}{\delta_j A d^{(j)} \cdot d^{(j)}} \end{aligned}\]上式的第四个等号右边,利用了 A 正交性质,使得添加项与 \(A d^{(j)}\) 点积后为 0。通过上式的推导,可知 \(\delta_j = -\alpha^{(j)}\),于是就有
\[e^{(0)} = - \sum \alpha^{(i)} d^{(i)}\]从几何意义上看,任选初始点,其初始误差都可表示为一组 A-正交向量的线性组合,且系数为 \(\alpha^{(i)}\) 。这样每次迭代沿着 \(d^{(i)}\) 前进长度 \(\alpha^{(i)}\),经过 k 次迭代后的误差为
\[e^{(k)} = e^{(0)} + \sum_i^{k-1}\alpha^{(i)}d^{(i)} = \sum_i^{n-1}\delta_i d^{(i)} - \sum_i^{k-1}\delta_i d^{(i)} = \sum_{i=k}^{n-1}\delta_i d^{(i)}\]n次迭代后,误差量被完全消除,即收敛。现在的问题是如何找到这样一组A-正交的向量作为每次迭代的方向。我们知道,若已知空间中的一组基,那么可以应用一种名为格拉姆施密特正交化的技术算出一组正交基。利用相似的原理可以计算出一组 A-正交的向量,名为共轭格拉姆施密特正交化。
假设已知一组基向量 \(u_i, i = 0,1,,,n-1\),利用公式
\[d^{(i)} = u_i + \sum \beta_{ik} d^{(k)}\]可以得到一组 A-正交向量 \(d^{(i)}, i = 0,1,,,n-1\)。为了计算 \(\beta\),使用 \(A d^{(j)}\) 点积上式两端
\[\begin{aligned} A d^{(j)}\cdot d^{(j)} &= A d^{(j)}\cdot u_i + \sum \beta_{ik} A d^{(j)}\cdot d^{(k)}\\ 0 &= A d^{(j)}\cdot u_i + \beta_{ij} A d^{(j)}\cdot d^{(j)}\\ \beta_{ij} &= -\frac{A d^{(j)}\cdot u_i}{A d^{(j)}\cdot d^{(j)}} \end{aligned}\]理论上来讲,任选一组基向量都能得到一组 A-正交向量,但是其中的复杂度还是划不来。
前面我们看到,经过 i 次迭代后
\[x^{(i)} = x^{(i -1)} + \alpha^{(i - 1)} d^{(i-1)} = x^{(0)} + \sum_{j=0}^{i-1} \alpha^{(j)}d^{(j)}\]其中 \(\sum_{j=0}^{i-1} \alpha^{(j)}d^{(j)}\) 是基向量组 \(d^{(j)}, j=0,1,,,i-1\) 的线性组合,并将这组向量张成的空间记为 \(D_i\),从而 \(x^{(i)}\) 可以看作是由初始值 \(x^{(0)}\) 和空间 \(D_i\) 中的一个向量相加得到的。而 \(x^{(0)}\) 与 \(D_i\) 中的所有向量相加得到的点组成超平面,记作 \(x^{(0)} + D_i\)。显然 \(x^{(i)}\) 属于此超平面,并且 \(x^{(i)}\) 是此超平面上使得 \(f(x)\) 最小的点,也是使得 \(\|e\|_A\) 最小的点。
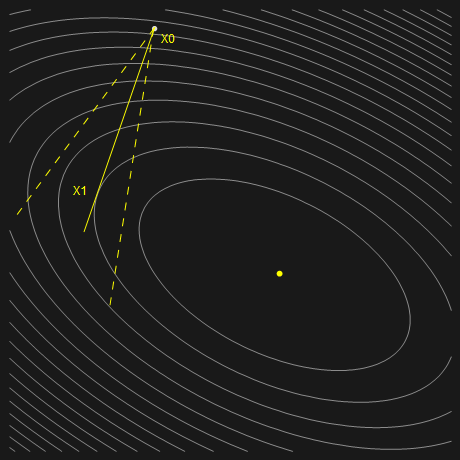
以二维情况为例,初始点 \(x^{(0)}\) 为平面上任意一点,\(d^{(0)}\) 为迭代方向,这时的超平面其实就是直线 \(x^{(0)} + k d^{(0)}, k \in R\)。显然直线上的某一点的函数值 \(f(x)\) 比其他点的函数值都小,这一点就是我们要找的 \(x^{(1)}\),并且容易理解,此直线相切于 \(x^{(1)}\) 所在的等高线(如果相交,那么就不满足 \(f(x)\) 取最小,如果相离,那么 \(x^{(1)}\) 就根本不在直线上,情况如下图所示)。类比到高维空间,超平面 \(x^{(0)} + D_i\) 相切于 \(x^{(i)}\) 所在的等高线超椭球。
另一方面,迭代 i 次后的残差 \(r^{(i)}\) 在 \(x^{(i)}\) 处与等高线相垂直,那么也就和超平面 \(x^{(0)} + D_i\) 相垂直,从而和 \(D_i\) 的每个基向量 \(d^{(j)}, j =0,1,,,i-1\) 相垂直。这一结论可以从公式推导得出
\[\begin{aligned} e^{(i)} &= \sum_{j = i}^{n - 1} \delta_j d^{(j)}\\ A d^{(k)}e^{(i)} &= \sum_{j = i}^{n - 1} \delta_j A d^{(k)}d^{(j)}\\ A e^{(i)}d^{(k)} &= \sum_{j = i}^{n - 1} \delta_j A d^{(k)}d^{(j)}\\ -r^{(i)}\cdot d^{(k)} &= \sum_{j = i}^{n - 1} \delta_j A d^{(k)}d^{(j)}\\ r^{(i)}\cdot d^{(k)} &= 0 \quad (if \quad k < i) \end{aligned}\]同样可以证明 \(r^{(i)}\) 垂直于向量组 \(u_j, j = 0,1,,,i-1\)
\[\begin{aligned} d^{(j)} &= u_j + \sum \beta_{jk} d^{(k)}\\ r^{(i)} \cdot d^{(j)} &= r^{(i)}\cdot u_j + \sum_{k=0}^{j-1} \beta_{jk} r^{(i)}\cdot d^{(k)}\\ 0 &= r^{(i)}\cdot u_j \quad (if \quad i > j) \end{aligned}\]另外,当 \(i = j\) 时,可以证明
\[d^{(i)}\cdot r^{(i)} = u_i \cdot r^{(i)}\]共轭梯度法
根据公式
\[0 = r^{(i)} \cdot u_j , \quad (if \quad i > j)\]若用 \(r^{(i)}\) 代替所有 \(u_i\),那么就有
\[0 = r^{(i)} \cdot r^{(j)} , \quad (if \quad i > j)\]也就是说,第 i 步迭代的 \(r^{(i)}\) 正交于之前的所有 \(r^{(j)}, j < i\),这就说明向量组 \(r^{(i)}, i = 0,1,,,n-1\) 能张成空间,符合作为基向量的条件。
根据前面的结论
\[\beta_{ij} = -\frac{A d^{(j)}\cdot u_i}{A d^{(j)}\cdot d^{(j)}} = -\frac{A d^{(j)}\cdot r^{(i)}}{A d^{(j)}\cdot d^{(j)}}\]并且
\[\begin{aligned} r^{(j+1)} &= -A e^{(j+1)} \\ {}&=-A(e^{(j)} + \alpha^{(j)} d^{(j)})\\ {}&=-A e^{(j)} - \alpha^{(j)} A d^{(j)}\\ {}&=r^{(j)} - \alpha^{(j)} A d^{(j)} \end{aligned}\]上式两边同时点乘 \(r^{(i)}\)
\[r^{(j+1)} \cdot r^{(i)} = r^{(j)} \cdot r^{(i)} -\alpha^{(j)} A d^{(j)}\cdot r^{(i)}\]由于\(r^{(i)}\cdot r^{(j)} = 0, if i \neq j\) 这里存在3种情况
- 当 \(i = j\) 时,\(0= r^{(j)} \cdot r^{(i)} -\alpha^{(j)} A d^{(j)}\cdot r^{(i)}\)
- 当 \(i = j + 1\) 时,\(r^{(j+1)} \cdot r^{(i)} = -\alpha^{(j)} A d^{(j)}\cdot r^{(i)}\)
- 否则,\(0 = -\alpha^{(j)} A d^{(j)}\cdot r^{(i)}\)
于是有
\[A d^{(j)}\cdot r^{(i)} = \begin{cases} \frac 1 {\alpha^{(j)}} r^{(j)}\cdot r^{(i)} \quad (i = j)\\ -\frac 1 {\alpha^{(j)}} r^{(j+1)}\cdot r^{(i)} \quad (i = j+1)\\ 0 \quad other \end{cases}\]由共轭格拉姆施密特正交化公式
\[d^{(i)} = u_i + \sum \beta_{ik} d^{(k)}\]可以发现,\(\beta_{ik}\) 的第二个指标永远不会大于第一个指标,也就是说 \(\beta_{ij}\) 中 \(j < i\) 恒成立。这就意味着前面分割的三种情况只剩下两种 \(i = j+ 1\) or \(i >j+1\),于是
\[\beta_{ij} = -\frac{A d^{(j)}\cdot r^{(i)}} {A d^{(j)}\cdot d^{(j)}} = \begin{cases} \frac{r^{(j+1)}\cdot r^{(i)}}{\alpha^{(j)} A d^{(j)}\cdot d^{(j)}} \quad (i = j+1)\\ 0 \quad (i > j+ 1) \end{cases}\]对于 \(i = j+ 1\) 这种情况
\[\beta_{i, i-1} = \frac{r^{(i)}\cdot r^{(i)}} {\alpha^{(i-1)} A d^{(i-1)} \cdot d^{(i-1)}}\]将最开始推导的
\[\alpha^{(i-1)} = \frac{r^{(i-1)}\cdot d^{(i-1)}}{A d^{(i-1)}\cdot d^{(i-1)}}\]代入 \(\beta_{i, i-1}\) ,并将其简记为 \(\beta_i\) 可得
\[\beta_i= \frac{r^{(i)}\cdot r^{(i)}} {r^{(i-1)}\cdot r^{(i-1)}}\]综合前面的讨论,最后总结共轭梯度算法的计算过程:
initialize: \(x^{(0)} = 0, r^{(0)} = b- A x^{(0)} = b, d^{(0)} = r^{(0)}\)
loop while not converged
\[\begin{aligned} \alpha^{(i)} &= \frac{r^{(i)} \cdot d^{(i)}}{A d^{(i)}\cdot d^{(i)}}\\ x^{(i+1)} &= x^{(i)} + \alpha^{(i)} d^{(i)}\\ r^{(i+1)} &= r^{(i)} - \alpha^{(i)} A d^{(i)}\\ \beta_{i+1} &= \frac{r^{(i+1)}\cdot r^{(i+1)}}{r^{(i)}\cdot r^{(i)}}\\ d^{(i+1)} &= r^{(i+1)} + \beta_{i+1} d^{(i)} \end{aligned}\]end