最速下降法解线性方程组
算法推导
已知待求解的线性方程组
\[A x = b\]其中 A 为对称正定矩阵,x 为向量。上述问题等价于求解如下二次型的极小值
\[f(x) = \frac 1 2 x^T A x - x^T b\]为了说明这种关系,考虑对 \(f(x)\) 求导
\[f'(x) = \frac 1 2 A x + \frac 1 2 x^T A - b\]由于 A 为对称正定矩阵,所以
\[f'(x) = A x - b\]而 \(f(x)\) 取得极小值的条件是 \(f'(x) = 0\),即 \(A x - b =0\),这就说明两个问题其实是等价的。事实上,若 A 为二阶矩阵,那么 \(f(x)\) 的图像是空间上的抛物面,且开口向上
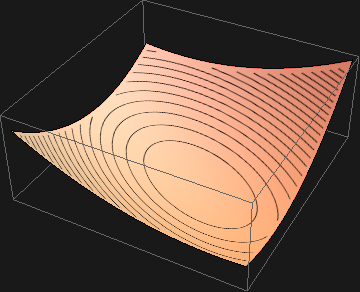
而其等高线则如下图所示,在中间的一点处,函数取得最小值。

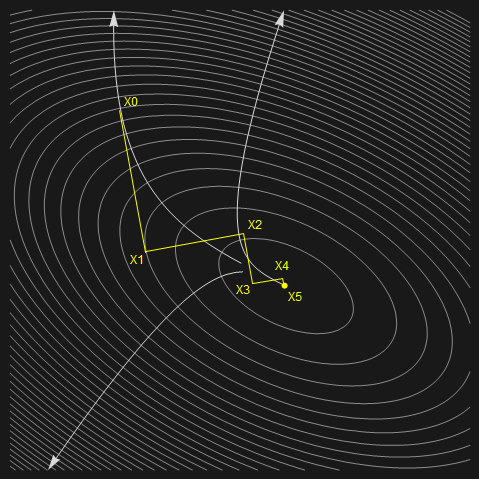
为了找到 \(f(x)\) 的极小值,可以考虑先假设一个初始值 \(x^{(k)}\),然后沿 \(f(x)\) 在 \(x^{(k)}\) 处的负梯度方向移动,这是函数值下降最快的方向。假设移动的长度为 \(\alpha^{(k)}\),到达点新的点
\[x^{(k+1)} = x^{(k)} - \alpha^{(k)} f'(x^{(k)})\]另一方面,\(-f'(x) = b - A x^{(k)}\) 是将 \(x = x^{(k)}\) 代入 \(A x = b\) 后的残差,若是令 \(r^{(k)} = b - A x^{(k)}\) ,则有
\[x^{(k + 1)} = x^{(k)} + \alpha^{(k)} r^{(k)}\]为了确定步长 \(\alpha^{(k)}\) 的大小,考虑到 \(f(x^{(k+1)})\) 应该关于 \(\alpha^{(k)}\) 取极小值(不然为什么要取这样的 \(\alpha^{(k)}\)),也就是必须满足
\[\frac{\mathrm{d} f( x^{(k+1)})} {\mathrm{d} \alpha^{(k)}} = \frac{\mathrm{d} f( x^{(k+1)})} {\mathrm{d} x^{(k+1)}} \frac{\mathrm{d} x^{(k+1)}} {\mathrm{d} \alpha^{(k)}} = 0\]考虑到前面推导的 \(x^{(k+1)}\) 与 \(\alpha^{(k)}\) 的关系,上式又可写成
\[f'(x^{(k+1)}) \cdot (-f'(x^{(k)})) = 0\]再考虑到 \(r^{(k)} = -f'(x^{(k)})\) ,于是有
\[\begin{align} r^{(k+1)} \cdot r^{(k)} &= 0\\ (b- A x^{(k+1)}) \cdot r^{(k)} &= 0\\ (b - A (x^{(k)} + \alpha^{(k)} r^{(k)})) \cdot r^{(k)} &= 0\\ (b- A x^{(k)} - A \alpha^{(k)} r^{(k)})\cdot r^{(k)} &= 0\\ r^{(k)} \cdot r^{(k)} &= A \alpha^{(k)} r^{(k)}\cdot r^{(k)}\\ \alpha^{(k)} &= \frac{r^{(k)} \cdot r^{(k)} }{A r^{(k)}\cdot r^{(k)}} \end{align}\]综合前面的讨论,下面给出最速下降法的伪码(其中的乘法为点积):
initialize x, r = b - A x, epsilon
while(check(r) > epsilon){
alpha = r * r / (A * r * r)
x = x + alpha * r
r = b - A x
}
直观地看,整个算法迭代路线如下图所示
收敛性分析
首先定义迭代过程中 \(x\) 的近似值与精确值间的误差量
\[e^{(k)} = x^{(k)} - x\]由于 \(r^{(k)} = b -A x^{(k)}\) 以及 \(0 = b - A x\), 可知
\[r^{(k)} = -A e^{(k)}\]下面考虑最简单的情况,即假设 \(e^{(k)}\) 是 A 的特征向量,且对应的特征值为 \(\lambda^{(k)}\)。那么
\[r^{(k)} = -A e^{(k)} = - \lambda^{(k)} e^{(k)}\]又由于
\[A r^{(k)} = -A \lambda^{(k)} e^{(k)} = - \lambda^{(k)} \lambda^{(k)} e^{(k)} = \lambda^{(k)} r^{(k)}\]所以,\(r^{(k)}\) 也为 A 的特征向量,对应的特征值也为 \(\lambda^{(k)}\)。这时将迭代公式两边同时减去 \(x\),可得
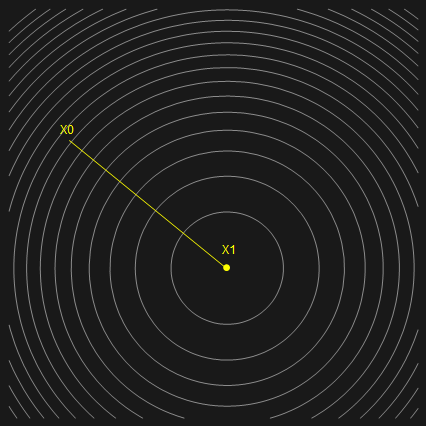
\[\begin{align} x^{(k +1 )} - x &= x^{(k)} - x + \alpha^{(k)} r^{(k)}\\ e^{(k+1)} &= e^{(k)} + \alpha^{(k)} r^{(k)} \\ {}&=e^{(k)} + \frac{r^{(k)} \cdot r^{(k)} }{A r^{(k)}\cdot r^{(k)} }(-A e^{(k)})\\ {}&=e^{(k)} + \frac{r^{(k)} \cdot r^{(k)} }{\lambda^{(k)} r^{(k)}\cdot r^{(k)} }(-\lambda^{(k)} e^{(k)})\\ {}&=0 \end{align}\]也就是说,只需经过一次迭代,即可达到精确解。从几何直观来说,点 \(x^{(k)}\) 刚好落在二次型形成的超抛物面的椭圆形等高线的轴上,这时残差向量 \(e^{(k)}\) 指向椭圆中心,于是选取合适的 \(\alpha^{(k)}\) 可以直接将 \(x^{(k+1)}\) 定位到椭圆中心,即超抛物面的极小点。过程如下图所示:

现在考虑稍微复杂一点的情况,即 \(e^{(k)}\) 为一般向量。可以证明矩阵 A 的特征向量张成整个空间,于是 \(e^{(k)}\) 可以用 A 的特征向量的线性组合表示为
\[e^{(k)} = \sum \xi_i \nu_i\]其中 \(\nu_i (i=1,2,,,n)\) 为一组正交单位向量(可以证明对任意对称矩阵,都存在这样一组正交单位特征向量)。正交向量组具有性质
\[\nu_i \cdot \nu_j = \left\{ \begin{aligned} 0& \quad i = j\\ 1& \quad i \neq j \end{aligned} \right.\]利用正交向量组,残差可以表示为
\[r^{(k)} = -A e^{(k)} = - \sum \xi_i A \nu_i = - \sum \xi_i \lambda_i \nu_i\]这时再考虑误差迭代格式
\[\begin{align} e^{(k+1)} &= e^{(k)} + \alpha^{(k)} r^{(k)}\\ &=e^{(k)} + \frac{r^{(k)} \cdot r^{(k)} }{A r^{(k)}\cdot r^{(k)}} r^{(k)} \end{align}\]其中
\[r^{(k)}\cdot r^{(k)} = \sum \xi_i \lambda_i \nu_i \cdot \sum \xi_j \lambda_j \nu_j = \sum \xi_i^2 \lambda_i^2\] \[\begin{align} A r^{(k)} \cdot r^{(k)} &= \sum \xi_i \lambda_i A \nu_i \cdot \sum \xi_j \lambda_j \nu_j\\ &= \sum \xi_i \lambda_i^2 \nu_i \cdot \sum \xi_j \lambda_j \nu_j\\ &= \sum \xi_i^2 \lambda_i^3 \end{align}\]代入后得到
\[e^{(k+1)} = e^{(k)} + \frac{\sum \xi_i^2 \lambda_i^2}{\sum \xi_i^2 \lambda_i^3} r^{(k)}\]如果假设 A 的所有特征值都相同,那么
\[\begin{align} e^{(k+1)} &= e^{(k)} + \frac{\lambda^2\sum \xi_i^2 }{\lambda^3\sum \xi_i^2} (-\lambda \sum xi_i \nu_i)\\ &= e^{(k)} - \sum \xi_i \nu_i\\ &= 0 \end{align}\]可以看到,又只经过一次迭代便达到精确解。从几何意义上来看,要求 A 的所有特征值都相同,意味着二次型的超抛物面的等高线为超球,这时,无论在何处取初始值,其残差方向都指向球心,选取合适的步长,即可一次迭代便达到精确解。过程如下图所示:
一般情况下的收敛性分析
前面,我们对误差的定义为
\[e^{(k)} = x^{(k)} - x\]这就意味着,只要是与精确解 \(x\) 距离相等的一圈点,它们的误差都是一样的。但实际上除非矩阵 A 的特征值都相同,即等高线为圆形,否则这些点上的函数值距离极小值并不相同。为了改进这种不太合适声明,下面新定义一种误差函数
\[||e||_A = A e \cdot e\]可以证明上述误差定义满足条件——同一等高线上的点,误差值相同。下面推导影响误差收敛性的因素
\[\begin{align} ||e^{(k+1)}||_A &=A e^{(k)}\cdot e^{(k)}\\ &=A(e^{(k)} +\alpha^{(k)})\cdot (e^{(k)} +\alpha^{(k)})\\ &=A e^{(k)}\cdot e^{(k)} + 2 \alpha^{(k)} A e^{(k)} \cdot r^{(k)} + (\alpha^{(k)})^2 A r^{(k)} \cdot r^{(k)}\\ &=||e^{(k)}||_A + 2 \frac{r^{(k)} \cdot r^{(k)}} {A r^{(k)}\cdot r^{(k)}} (-r^{(k)}\cdot r^{(k)}) + \left(\frac{r^{(k)} \cdot r^{(k)}} {A r^{(k)}\cdot r^{(k)}} \right)^2 A r^{(k)}\cdot r^{(k)}\\ &=||e^{(k)}||_A - \frac{r^{(k)} \cdot r^{(k)}} {A r^{(k)}\cdot r^{(k)}}\\ &=||e^{(k)}||_A \left(1 - \frac{(r^{(k)} \cdot r^{(k)})^2}{A r^{(k)} \cdot r^{(k)} A e^{(k)} \cdot e^{(k)}}\right)\\ &=||e^{(k)}||_A \left(1 - \frac{(\sum \xi_i^2 \lambda_i^2)^2}{\sum \xi_i^2 \lambda_i^3 \sum \xi_i^2 \lambda_i}\right) \end{align}\]若令
\[\omega^2 = \left(1 - \frac{(\sum \xi_i^2 \lambda_i^2)^2}{\sum \xi_i^2 \lambda_i^3 \sum \xi_i^2 \lambda_i}\right)\]可得简化形式
\[||e^{(k+1)}||_A = ||e^{(k)}||_A \omega^2\]现在考虑我们之前提到的两种简化情况
- 当误差 \(e^{(k)}\) 为 A 的特征向量时。意味着 \(\xi_i (i=1,,,n)\) 除了一项为1,其余项都为0。此时 \(\omega=0\),只需迭代一步即收敛。
- 当 A 的所有特征值都相同时,\(\omega=0\),也是迭代一步收敛。
可见上面推导的公式蕴含之前假设的特殊情况。而在一般情况下,只要 \(\|\omega\| < 1\),则算法就一定收敛。