支持向量机
考虑属于两个类别的样本集合
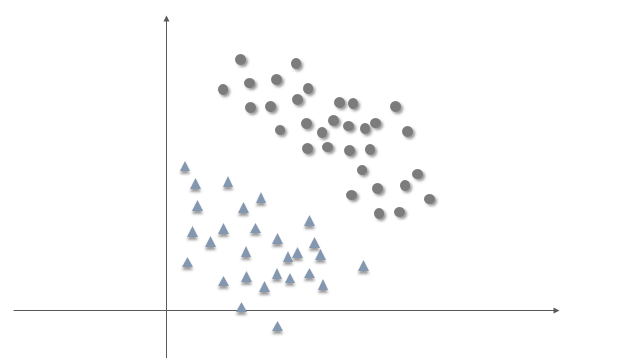
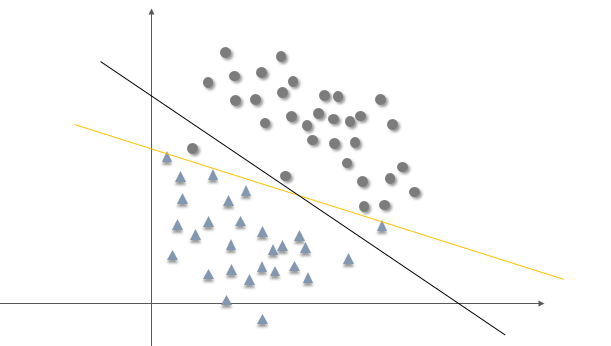
\[S = \{(x^{(i)}, y_i )\,\mid i = 1,,,n\}\]其中 \(x^{(i)}\) 是维度为 d 的特征,\(y_i\) 表示样本类别,等于 1 或者 -1。如果两个类别线性可分,那么将特征点集合投影到二维面上大致如下图所示
为了对数据进行分类,我们可以选择一个超平面对两类数据进行切割,显然这里有无数种切割方式,但是有的分隔面比其他面效果更好。支持向量机的任务就是找到这样一个分隔面,使得所有特征点到它的最小距离达到最大值,或者换句话说就是,使得两类特征点到分隔面的最小距离相等,如下图所示
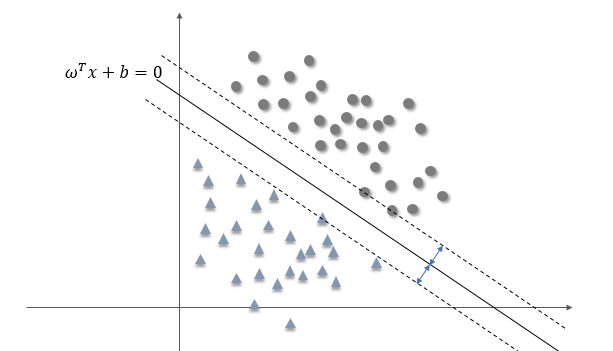
假设上图中的实线即为这样的超平面,设其方程为
\[\omega^T x +b = 0\]我们说这样的分隔面使得特征点到它的最小距离最大,后续的讨论都将围绕这一目标来进行。
为了计算空间中一个点到超平面的距离,我们考虑如下位置关系,假设点 \(x^{(i)}\) 离超平面的距离为 \(\gamma_i\),我们过这一点作一条垂线,垂足为 \(x_p\),显然 \(x_p\) 满足方程
\[\omega^T x_p + b = 0\]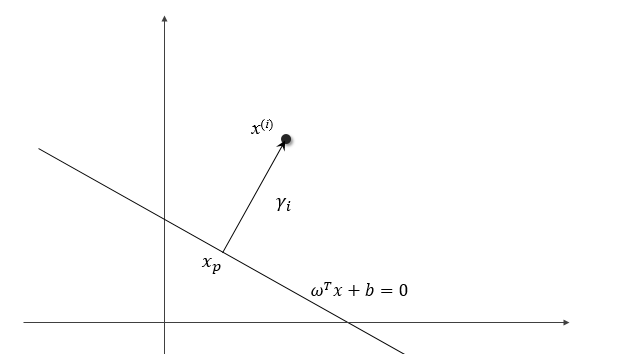
并且可以证明从 \(x_p\) 指向 \(x^{(i)}\) 的方向为 \(\omega\) ,于是存在下述关系
\[x^{(i)} = x_p + \gamma_i \frac{\omega}{\|\omega\|}\]将 \(x^{(i)}\) 代入函数 \(f(x) = \omega^T x + b\)
\[\begin{aligned} f(x^{(i)}) &= \omega^T (x_p + \gamma_i \frac{\omega}{\|\omega\|}) + b\\ &= \omega^T x_p + b + \gamma_i \|\omega\|\\ &=\gamma_i \|\omega\|\\ \gamma_i& =\frac{f(x^{(i)})}{\|\omega\|} =\frac{\omega^T}{\|\omega\|}x^{(i)} + \frac{b}{\|\omega\|} \end{aligned}\]对于第二个类别的数据,\(x^{(i)}\) 位于超平面的另一边,如下图
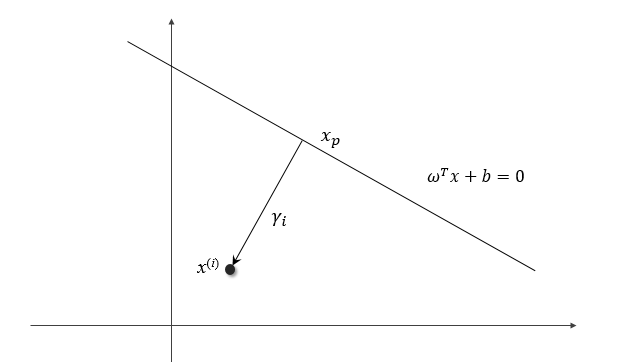
则类似地有
\[x^{(i)} = x_p - \gamma_i \frac{\omega}{\|\omega\|}\] \[\gamma_i =-\left( \frac{\omega^T}{\|\omega\|}x^{(i)} + \frac{b}{\|\omega\|}\right)\]设第一个类别的标签为 \(y_i = 1\),第二类别为 \(y_i = -1\),那么可以将距离统一写成
\[\gamma_i =y_i \left(\frac{\omega^T}{\|\omega\|}x^{(i)} + \frac{b}{\|\omega\|}\right)\]定义所有特征到超平面的最小距离为 \(\gamma\)
\[\gamma = \min_{i=1,,,n} \gamma_i\]为了找到最合适的分隔面,我们定义的目标就是搜寻 \(\omega, b\), 使得上述得到的最小间隔有最大的值,即
\[\max_{\omega, b}\,\gamma\]其中 \(\gamma\) 应满足
\[\quad y_i \left(\frac{\omega^T}{\|\omega\|}x^{(i)} + \frac{b}{\|\omega\|}\right) \ge \gamma\,\,,\, i = 1,,,n\]这就是优化问题的约束条件。考虑将不等式两边同时乘以 \(\omega\)
\[\quad y_i \left(\omega^Tx^{(i)} + b\right) \ge \|\omega\|\gamma\,\,,\, i = 1,,,n\]由下面两个方程定义的超平面本质上是一样的
\[m\omega^T x + m b = 0\\ \omega^T x + b = 0\]但是它们法向量的2-范数的关系却是 \(\|m\omega\| =\sqrt{m} \|\omega\|\),也就是说,缩放 \(\omega\) 并不会对我们要找的超平面造成实质的影响,于是我们可以令
\[\|\omega\| \gamma = 1\]那么优化问题就变成了
\[\max_{\omega, b} \frac 1 {\|\omega\|}\\ s.t.\quad g(x^{(i)}) \le 0 ,\, i = 1,,,n\]其中 \(g(x^{(i)}) =- y_i(\omega^T x^{(i)} + b)+1\)。上面的问题也等价于
\[\min_{\omega, b} \frac 1 2 \|\omega\|^2\\ s.t.\quad g(x^{(i)}) \le 0 ,\, i = 1,,,n\]这是一个有不等式约束的凸优化问题,可以利用拉格朗日乘子法求解,首先建立拉格朗日函数
\[L(\omega, b,\alpha) = \frac 1 2 \|\omega\|^2 + \sum_{i=1}^n \alpha_i [- y_i(\omega^T x^{(i)} + b)+1]\]其中 \(\alpha\) 为拉格朗日乘子向量,规定它的每个分量都为非负值。然后定义
\[\Theta_p(\omega, b) = \max_{\alpha_i \ge 0} L(\omega, b, \alpha)\]由于 \(\alpha_i\) 的任意性,如果任一约束条件得不到满足,都能使拉格朗日函数趋于无穷大,而当所有约束条件都满足时,有
\[\Theta_p(\omega, b) = \frac 1 2 \|\omega\|^2\]所以上述带不等式约束的凸优化问题,可以转换成不带约束的凸优化问题
\[\min_{\omega, b} \max_{\alpha_i \ge 0} L(\omega, b, \alpha)\]前面的约束 \(g(x_i) \le 0\) 在这里是自然成立的,因为如果有一项不成立,将取不到极小值。如果满足一定的条件,那么上述问题又可转换成其对偶形式
\[\max_{\alpha_i \ge 0}\min_{\omega, b} L(\omega, b, \alpha)\]一般来讲,原问题的解都会大于其对偶问题,这被称为弱对偶,但是当原问题的目标函数为凸函数时,常常获得强对偶,即两者相等。另一方面为了判断获得的解是否是最优解,需要满足 KKT 条件
\[\begin{aligned} \frac{\partial L}{\partial \omega_i} = 0&, i = 1,,,d \quad(1)\\ \alpha_i g(x^{(i)}) = 0 &,i = 1,,,n \quad (2)\\ g(x^{(i)}) \leq 0&, i = 1,,,n \quad (3) \\ \alpha_i \geq 0&, i=1,,,n \quad (4) \end{aligned}\]注意条件 (2)(3) ,如果 \(g(x^{(i)}) < 0\) 严格成立,那么 \(\alpha_i\) 必然等于 0。再结合下图

可以发现,对于大多数的特征点来讲,\(g(x^{(i)})\) 都是小于 0 的,也就意味着这些点对应的 \(\alpha_i\) 都等于 0,这是支持向量机的一个重要性质。
在继续推导拉格朗日对偶问题的公式之前,我们先来考虑支持向量机的软件隔分类问题,简单的说就是,我们得到的特征可能会出现噪声,产生了少量异常点,导致严格的线性可分条件不存在 或者说,即便能够找到分隔面,但是总体来看并不理想,还不如放开一些异常点,让大多数点能正常分类。
为了获取这种能力,可以考虑对约束条件放宽限制,即
\[y_i(\omega^T x^{(i)} + b) \ge 1 - \xi_i ,\quad i = 1,,,n, \quad\xi_i \ge 0\]也就是说,允许一些点距离分隔面小于 1,甚至越过分隔面。但不能无限制的放纵,而是相应地在优化目标函数上添加一个惩罚项,即得到
\[\min_{\omega,\xi} \frac 1 2 \|\omega\|^2 + C\sum_{i=1}^n \xi_i \\ s.t.\quad y_i(\omega^T x^{(i)} + b) \ge 1 - \xi_i ,\quad i = 1,,,n\\ \quad\xi_i \ge 0,\quad i = 1,,,n\]相应的拉格朗日函数为
\[L(\omega, b, \xi, \alpha, \beta) = \frac 1 2 \|\omega\|^2 + C\sum_{i=1}^n \xi_i + \sum_{i=1}^n \alpha_i [-y_i(\omega^T x^{(i)} + b) + 1 - \xi_i]-\sum_{i=1}^n\beta_i \xi_i\]并且拉格朗日对偶问题可以修改为
\[\max_{\alpha_i \ge 0,\beta_i\ge 0}\min_{\omega, b, \xi} L(\omega, b,\xi, \alpha,\beta)\]先求解 \(L(\omega, b,\xi, \alpha,\beta)\) 关于 \(\omega, b, \xi\) 的极值
\[\nabla_\omega L = \omega - \sum_{i=1}^n \alpha_i y_i x^{(i)} = 0\] \[\frac{\partial L}{\partial b} = \sum_{i=1}^n \alpha_i y_i = 0\] \[\frac{\partial L}{\partial \xi_i} = C -\alpha_i -\beta_i = 0\]于是可以得到
\[\omega = \sum_{i=1}^n \alpha_i y_i x^{(i)}\\ \sum_{i=1}^n \alpha_i y_i = 0\\ C =\alpha_i +\beta_i\]然后设拉格朗日函数的极值为 \(W(\alpha)\),则有
\[\begin{aligned} W(\alpha) &= \frac 1 2 \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j <x^{(i)}, x^{(j)}> +\sum_{i=1}^n (\alpha_i + \beta_i)\xi_i \\ &-\sum_{i=1}^n \alpha_i y_i\sum_{j=1}^n \alpha_j y_j <x^{(i)}, x^{(j)}> + \sum_{i=1}^n \alpha_i -\sum_{i=1}^n \alpha_i \xi_i - \sum_{i=1}^n \beta_i \xi_i\\ &=-\frac 1 2 \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j <x^{(i)}, x^{(j)}> + \sum_{i=1}^n \alpha_i \end{aligned}\]其中 \(<x^{(i)}, x^{(j)}>\) 表示两个向量的内积。可以看到虽然引入了软间隔分类模型,待优化目标函数却不含任何与软间隔参数相关的量,这也使得求解简单了许多。但是引入新的拉格朗日乘子 \(\beta\) 也要满足 KKT 条件,即
\[\beta_i \xi_i = 0\]将 \(\beta_i = C - \alpha_i\) 代入得
\[(C - \alpha_i)\xi_i=0\]也就是说当 \(\xi_i > 0\) 时,\(\alpha_i=C\),而当 \(\xi_i=0\) 时,\(\alpha_i <C\) ,这是由于 \(\beta_i \ge 0\) 恒成立。
于是,最终我们的问题就化为
\[\max_{\alpha} W(\alpha)\\ s.t.\quad 0 \le \alpha_i \le C,\quad i = 1,,,n\\ \sum_{i=1}^n \alpha_i y_i=0 ,\quad i=1,,,n\]下一部分,我们将考虑如何求解这个凸优化问题。
后记:本文参考自 Andrew Ng 的机器学习讲义,以及一些 blog 的内容,结合自己的理解,主要工作是从最简单的目标出发,一步步推导支持向量机的有关方程,尽量做得流畅,并且有说服力。我觉得没有必要引入函数间隔,几何间隔这两个名词,尽管一开始就使用了这样的概念,但是少定义些东西我认为还是有好处的。然后核函数的内容也没有涉及,这在以后的文章中补上。写这篇文章的小插曲:之前就写了一篇类似的,但后来觉得不好,就又重写了这篇,然后在把本文剪切到项目的 _post 文件夹的时候,由于没有停止 jekyll 服务,结果被原来的那篇给覆盖了。。然后心里不服啊,第二天又才写出这篇。想不到我竟然会中这招,本来什么 Onedrive,github 这些都用上了的,结果还是一个不小心,都是教训。